Radar Installation
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 42242 | Accepted: 9359 |
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
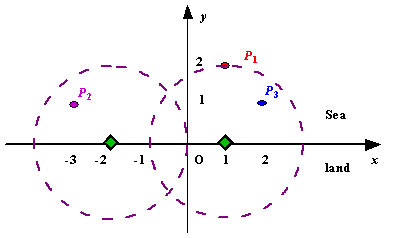
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
水题!贪心的思想 #include<stdio.h> #include<iostream> #include<algorithm> #include<math.h> using namespace std; struct pti{ double x,y,min,max; } num[1050],temp; #define eps 1e-10 bool cmp(pti a,pti b) { if(b.min-a.min>=eps) return true; return false; } int main () { int i,n,j,sum,flag=1,re; double min,max,te,r; while(scanf("%d%lf",&n,&r)!=EOF&&n&&r) { if(r<=0) re=0; else re=1; for(i=1;i<=n;i++) { scanf("%lf%lf",&num[i].x,&num[i].y); if(((r>=num[i].y))&&re) { te=r*r-num[i].y*num[i].y; num[i].min=num[i].x-sqrt(te); num[i].max=num[i].x+sqrt(te); } else { re=0; } } if(re) { sort(num+1,num+n+1,cmp); /*for(i=1;i<=n;i++) printf("%lf ",num[i].min); */ sum=1; min=num[1].min; max=num[1].max; for(i=2;i<=n;i++) { if(max-num[i].min>=eps) { if(max-num[i].max>=eps) max=num[i].max; } else { sum++; min=num[i].min; max=num[i].max; } } printf("Case %d: %d\n",flag++,sum); } else { sum=-1; printf("Case %d: %d\n",flag++,sum); } } return 0; }
























 1108
1108

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








