继上一篇基本最小二乘法和带部分空间约束的最小二乘法,它们要么易过拟合,要么不易求解,下面介绍 l2约束的最小二乘法,又叫正则化最小二乘法,岭回归。
一个模型的复杂程度与系数有关,最简单的模型是直接给所有系数赋值为0,则该模型总会预测出0值,模型虽然足够简单,但是没有意义,因为它不能有效预测。
定义模型的复杂度为:
由于我们的目的是使模型不要过于复杂,所以让上述值小是有意义的,因此新的目标函数为:
即
前一项为数据拟合程度的惩罚项,数据拟合的越好,该项值越小,但是也有可能过于拟合样本数据导致模型过于复杂;后一项为模型复杂程度的惩罚项,当模型越复杂,该项值越大,即为了最小化目标函数,我们要让数据拟合的好同时模型不至于太复杂。其实就是在基本最小二乘法的目标函数中增加了一个正则化项,所谓正则化,可以看为函数光滑性。将上式目标函数进行参数求偏微分,解得:
下面从参数空间约束的角度介绍 L2 约束的最小二乘法。
L2约束的最小二乘法是以参数空间的原点为圆心,在一定半径范围内(一般为超球)内进
 正则化最小二乘法
正则化最小二乘法





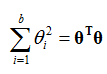
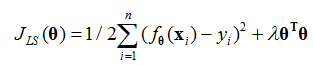
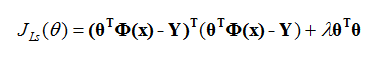
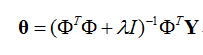

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 3502
3502

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








