(注:本文仅作为学习使用,若转载拷贝等引起的一切后果由读者自负。)
最近学习了McEliece公钥密码体制, 它是一种不对称加密算法,基于代数编码理论,使用了一系列纠错代码Goppa。这种加密系统使用Goppa代码作为专用密钥。其安全性基于纠错编码(error correcting codes)理论。
假设有长度1024的二元字符串,它有50个错误地方,则错误位置的情况就有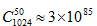
一、加密解密过程
假设通信双方分别是Bob和Alice,Bob首先选择一个生成矩阵G(该矩阵用于产生一个线性纠错码C,其码的重量为d),再选择一个k*k矩阵S(可逆矩阵),还有一个n*n矩阵P(可置换阵,这意味着P的每行每列都只有一个1)。我们定义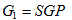
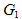
(a).现在Alice需要向Bob发送一个消息x,Alice则进行下面的操作:(1)她产生一个随机二元字符串e,其长度为n,重量为t;(2)计算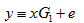
(b).Bob收到密文y,如何解密?(1)计算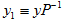
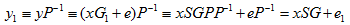
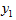


二、安全性简述
该公钥的安全性主要依赖于破解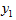

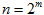
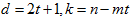
三、例子
Step 1:公钥私钥产生阶段:
生成矩阵G如下:
(熟悉线性纠错码的读者应该发现了,这个就是其实是[7,4]Hamming码)。Bob再选择私钥S、P,分别选择如下(注意:S一定要是可逆,P一定是置换阵)
通过S、G和P我们计算出公钥如下:

Step 2:密文产生阶段
假设Alice想向Bob发送消息m=(1,0,1,1),首先选择一个随机的错误码e,,假定e=(0,1,0,0,0,0,0),(为什么只有1个"1"呢?答:Hamming码的纠错能力有限,只可以纠1位)。运用公式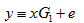
Step:解密阶段
Bob收到密文y后,计算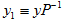
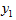

针对这个例子,我们发现其第六位是错的,纠正,得到

x就是我们所解密得到的明文了!
四、JAVA代码示例
针对上面的例子,笔者编写了一个JAVA程序来测试。该问题中具有非常多的矩阵运算,因此笔者采用了JAMA包来帮忙解决这个问题。JAMA的下载地址:http://math.nist.gov/javanumerics/jama/
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import Jama.Matrix;
public class McEliece {
private static Matrix G;
private static Matrix H;
private static Matrix S;
private static Matrix P;
private static Matrix G1;
private static Matrix e;
private static Matrix y;
private static Matrix y1;
private static Matrix x1;
private static Matrix x0;
private static Matrix x;
private final static int LENGTH = 4;
public void generator(int type) {
double[][] array = null;
double[][] arrayH = null;
if (type == 1) {
array = new double[][] { { 1, 0, 0, 0, 1, 1, 0 },
{ 0, 1, 0, 0, 1, 0, 1 }, { 0, 0, 1, 0, 0, 1, 1 },
{ 0, 0, 0, 1, 1, 1, 1 } };
arrayH = new double[][] { { 1, 1, 0 }, { 1, 0, 1 }, { 0, 1, 1 },
{ 1, 1, 1 }, { 1, 0, 0 }, { 0, 1, 0 }, { 0, 0, 1 } };
}
G = new Matrix(array);
H = new Matrix(arrayH);
}
public void CreateSandP() {
double[][] array = { { 1, 0, 0, 1 }, { 1, 1, 0, 1 }, { 0, 1, 0, 1 },
{ 1, 1, 1, 0 } };
S = new Matrix(array);
double[][] array1 = { { 0, 0, 1, 0, 0, 0, 0 }, { 1, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 1, 0, 0 }, { 0, 0, 0, 0, 0, 1, 0 },
{ 0, 0, 0, 0, 0, 0, 1 }, { 0, 1, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0 } };
P = new Matrix(array1);
}
private void Mod2(Matrix ma) {
for (int i = 0; i < ma.getRowDimension(); i++)
for (int j = 0; j < ma.getColumnDimension(); j++)
ma.set(i, j, Math.abs(((int) ma.get(i, j)) % 2));
}
public void CaculateG1() {
G1 = S.times(G).times(P);
Mod2(G1);
}
public void GenerErrorVector() {
double[][] array = { { 0, 1, 0, 0, 0, 0, 0 } };
e = new Matrix(array);
}
public void CaculateCiphertext() {
y = x.times(G1).plus(e);
Mod2(y);
}
public void decrypt() {
int ErrorPosition = 0;
y1 = y.times(P.inverse());
Mod2(y1);
Matrix Syndrome = y1.times(H);// 计算得到校验子
Mod2(Syndrome);
// 与校验矩阵对比,进行校正
for (int i = 0; i < H.getRowDimension(); i++) {
boolean flag = true;
for (int j = 0; j < H.getColumnDimension() && flag; j++) {
if (H.get(i, j) != Syndrome.get(0, j))
flag = false;
}
if (flag) {
ErrorPosition = i;
break;
}
}
System.out.println("错误的位置:" + ErrorPosition);
x1 = y1.copy();
x1.set(0, ErrorPosition,
(double) ((int) (y1.get(0, ErrorPosition)) + 1) % 2);
System.out.print("x1矩阵如下");
x1.print(0, 0);
x0 = x1.getMatrix(0, 0, 0, LENGTH - 1);
System.out.print("x0矩阵如下");
x0.print(0, 0);
System.out.print("解密得到明文:");
x = x0.times(S.inverse());
Mod2(x);
x.print(0, 0);
}
// test
public static void main(String args[]) {
/**
* 生成矩阵 这里我们使用2种hamming码
*/
McEliece test = new McEliece();
test.generator(1);
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
test.CreateSandP();
test.CaculateG1();
test.GenerErrorVector();
System.out.print("G1矩阵(公钥):如下");
G1.print(0, 0);
System.out.print("e矩阵:如下");
e.print(0, 0);
System.out.println("Alice: input message:");// 明文
try {
String secret = br.readLine();
double[][] array_x = new double[1][LENGTH];
for (int i = 0; i < LENGTH; i++) {
array_x[0][i] = Double.parseDouble(secret.charAt(i) + "");
}
x = new Matrix(array_x);
} catch (IOException e) {
e.printStackTrace();
}
// 计算得到的密文
test.CaculateCiphertext();
System.out.print("得到的密文:如下");
y.print(0, 0);
// 解密
System.out.print("Bob解密结果如下");
test.decrypt();
}
}
只给出了一个简单的实现程序,作为理解该密钥体制使用,不做其它用途。
笔者水平有限,欢迎交流!









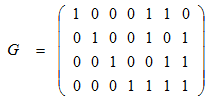
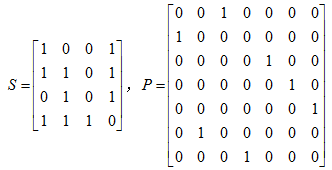
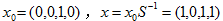


















 648
648

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








