数据结构 13-树的性质

目    录

1. 树中的节点数等于所有节点的度数加 1

2. 度为 m 的树中第 i 层 ( i≥1 ) 上至多有个节点。 

3. h>1 时候，高度为 h的 m 次树至多有 个节点。 

4. 具有 n 个节点的 m 次树的最小高度 h 为 ​ 

---

讲一下树的性质，为后面的二叉树做准备。 

1. 树中的节点数等于所有节点的度数加 1

        性质 1 其实非常好理解，如果是以层次的方式看待树，那么根节点的度，就等于第二层的节点数，第二层节点的度数之和，就等于第三层的节点数，以此类推。那么从第一层开始的每层节点度数和就等于从第二层开始的节点数之和，换言之，只是少了根节点。

2. 度为 m 的树中第 i 层 ( i≥1 ) 上至多有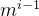个节点。

       性质 2 也很好理解。树的度 m，即整个树中节点度的最大值，意味着任意一个节点的度数都是小于等于 m 的。而节点的度数，就是分支的个数。

        那么简单推导一下：

        1）只有根节点的树，符合这一说法（i-1==0）

        2）层数大于 1 的树

             第一层 i==1 i-1==0   1

             第二层 i==2 i-1==1   最多 m

             第三层 i==3 i-1==2   最多 m*m       

..................................

3. h>1 时候，高度为 h的 m 次树至多有 个节点。

       请注意，h 一定是大于 1 时候该性质才成立，小于等于 1 时候是不成立的。

       从性质 2 可以知道，度为 m 的树中第i层(i≥1)上至多有个节点。

       那么树的节点数综合即 ， 即第 i 层的节点数之和，根据数学公式推导，高度为 h的 m 次树至多有 个节点。 

4. 具有 n 个节点的 m 次树的最小高度 h 为

       这个性质稍微复杂一点，我们来使用推导。

       根据性质 3，h>1 时候，高度为 h的 m 次树至多有 个节点。

       意味着  n <=，即  >= n(m-1) ；即 h 最小高度为