字符串的去除敏感字符

L:“shit”“fuck”“you” “hide” “york”
S:“shideshitmeshitfuckyou”
输出：S中包含的L一个单词，要求这个单词只出现一次，如果有多个出现一次的，输出第一个这样的单词
怎么做？

字符串匹配问题。
暴力的话，用字典树保存L，剩下来就是暴力破解了
构建字典树O(n_l), 暴力法的话，最多复杂度为：

$$O(n_{L平均长度}*m)$$

最近看AC自动机，其实这道题也是可以用AC自动机解决， 代码如下：

#include "stdio.h"
#include "string.h"

#define MAX_WORD_LEN 51

struct node{
    node *next[26];
    node *fail;
    bool isRead;
    bool isWord;
    int length;
    node() {
        isRead = false;
        isWord = false;
        fail = NULL;
        length = 0;
        for (int i = 0; i < 26; i++)
            next[i] = NULL;
    }
};
node* q[MAX_WORD_LEN];
node *root;
int head, tail;

void insert(char *str) {
    int len = strlen(str);
    node *p = root;
    int index;
    for (int i = 0; i < len; i++) {
        index = str[i] - 'a';
        if (p->next[index] == NULL)
            p->next[index] = new node();
        p->next[index]->length = p->length + 1;
        p = p->next[index];
    }
    p->isWord = true;
}

void build_ac(){
    q[tail++] = root;
    node *p, *temp;
    while (head != tail) {
        p = q[head++];
        for (int i = 0; i < 26; i++) {
            if (p->next[i] != NULL) {
                if (p == root) {
                    p->next[i]->fail = root;
                } else {
                    temp = p->fail;
                    while (temp != NULL && temp->next[i] == NULL)
                        temp = temp->fail;
                    if (temp == NULL)
                        p->next[i]->fail = root;
                    else
                        p->next[i]->fail = temp->next[i];
                }
                q[tail++] = p->next[i];
            }
        }
    }
}

void sensitify(char *str, int begin, int size) { 
    //  printf("%s, %d, %d\n", str, begin, size); 
    int len = strlen(str);
    int end = begin + size;
    while (end < len && begin < end) {
        str[begin++] = '*';
    }
}

void dealStr(char *str) {
    int len = strlen(str);
    node *p = root; // init status as root
    int index = 0;
    for (int i = 0; i < len; i++) {

        index = str[i] - 'a';
        while (p != NULL && p->next[index] == NULL)
            p = p->fail;

        if (p == NULL) {
            // root->fail = NULL, this means current chars cannot be accepted as any word.
            // reset the status as root.
            p = root;
        } else { // p->next[index] != NULL which means current status can accept this char.

            p = p->next[index];         // accept this char

            node *temp = p;
            while (temp != root) {
                if (temp->isWord) {
                    if (!temp->isRead)
                        temp->isRead = true;
                    else {
                        int size = temp->length;
                        int beginIndex = i - size + 1;
                        sensitify(str, beginIndex, size);
                    }
                }
                temp = temp->fail;  //this is the longest match, and some times we could not find uck in fuck, so we need to check fail pointer recursively 
            }
        }

    }
}

int main(){

    int ncase, num;
    //  scanf("%d", &ncase);
    ncase = 1;
    char keyword[51];
    char str[1024];
    while(ncase --) {
        head = tail = 0;
        root = new node();
        scanf("%d", &num);
        for (int i = 0; i < num; i++) {
            scanf("%s", keyword);
            insert(keyword);
        }
        build_ac();
        scanf("%s", str);
        dealStr(str);
        printf("%s\n", str);
    }
}

结果如下：

首先介绍一下字典树，形如下图：


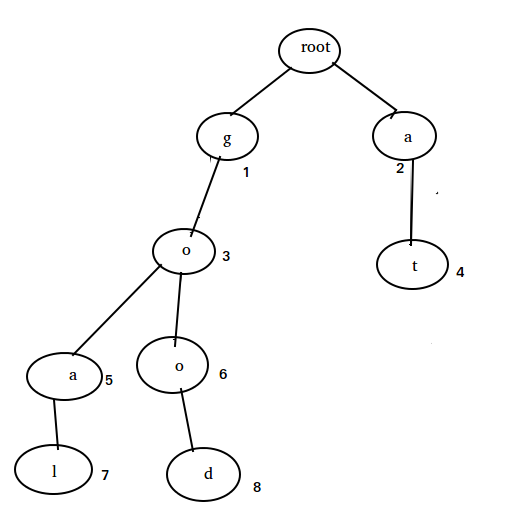
经常用于字符串的查找。具体代码为：

void insert(char *str) {
    int len = strlen(str);
    node *p = root;
    int index;
    for (int i = 0; i < len; i++) {
        index = str[i] - 'a';
        if (p->next[index] == NULL)
            p->next[index] = new node();
        p->next[index]->length = p->length + 1;
        p = p->next[index];
    }
    p->isWord = true;
}

其中 字符信息保存在 next[charIndex], 非空即为当前状态能接受该字符。或许将字符信息画在边上会更契合点。

接着是AC自动机

AC自动机的原理： 每一个节点都会有一个 fail 指针，表示当当前节点无法接受当前字符时，应该跳转的位置，一般为当前已接受字符的后缀式中能被AC机接受的字符串。通俗的来讲，当前字符串为goa时，后缀式“oa” “a”中“a”能被AC机接受（状态2）也就是状态5的 fail 指针应该是状态2. 如下图：

当输入字符串 input 为 goat 时，状态转至 5 时，由于当前状态无法处理字符 t，转到 fail 指针（状态2），查看是否能处理字符 t，正好能处理，进入状态4。这一过程读取 input 的指针并没有回退，也就是整个过程算法的时间复杂度为

$$O(n_{input\_len} * time_{average\_search\_time})$$
具体代码：

void dealStr(char *str) {
    int len = strlen(str);
    node *p = root; // init status as root
    int index = 0;
    for (int i = 0; i < len; i++) {

        index = str[i] - 'a';
        while (p != NULL && p->next[index] == NULL)
            p = p->fail;

        if (p == NULL) {
            // root->fail = NULL, this means current chars cannot be accepted as any word.
            // reset the status as root.
            p = root;
        } else { // p->next[index] != NULL which means current status can accept this char.

            p = p->next[index];         // accept this char

            node *temp = p;
            while (temp != root) {
                if (temp->isWord) {
                    if (!temp->isRead)
                        temp->isRead = true;
                    else {
                        int size = temp->length;
                        int beginIndex = i - size + 1;
                        sensitify(str, beginIndex, size);
                    }
                }
                temp = temp->fail;  //this is the longest match, and some times we could not find uck in fuck, so we need to check fail pointer recursively 
            }
        }

    }
}

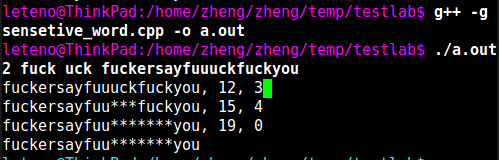
上面的 temp = temp->fail 的功能可以尝试把while 去掉， 尝试输入

2 fuck uck fuckersayfuuuckfuckyou

查看输出结果。

接下来是如何求 fail 指针。这里面要处理的问题是：
1） 确保失配时，跳转的 fail 指针应该是最长匹配。

首先算法的基本框架是BFS。
详细代码是

void build_ac(){
    q[tail++] = root;
    node *p, *temp;
    while (head != tail) {
        p = q[head++];
        for (int i = 0; i < 26; i++) {
            if (p->next[i] != NULL) {
                //TODO set p->next[i]->fail
                q[tail++] = p->next[i];
            }
        }
    }
}

重点在设置 fail 指针：

    if (p == root) {
        p->next[i]->fail = root;
    } else {
        temp = p->fail;
        while (temp != NULL && temp->next[i] == NULL)
            temp = temp->fail;
        if (temp == NULL)
            p->next[i]->fail = root;
        else //temp->next[i] != NULL which means temp can accept i just as p does.
            p->next[i]->fail = temp->next[i];
    }    

首先 root 下的所有可接受字符的 fail 指针为自身。
接着其他字符的 fail 指针为递归遍历父指针的 fail 指针中 能够接受当前字符，如果实在没有，则指向 root，表示当前的字符串不存在能接受的 keyword，重置状态。
举个例子：

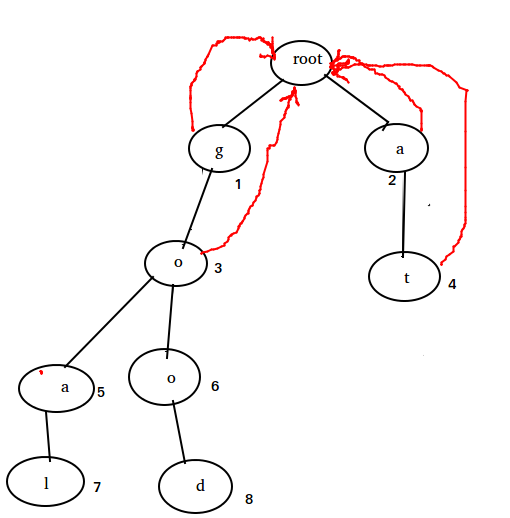
状态 3 i=a 的时候，查看状态 3 的 fail 指针 root，恰好能接受 i=a， 于是状态5 的 fail 指针指向状态 2.
其实 可以把一个节点的所有一系列（通过递归获取） fail 指针 看作状态机的同一个状态。感兴趣可以查看编译原理里面的状态转移。
那怎么确定当前取得的 fail 指针是最长匹配呢 比如 blue ue e ， blue e 的 fail 指针应该指向 ue 的 e， 而不是 e 呢？ 原因在他的父亲节点 u 的 fail 指针指向的是 ue 的 u，所以 blue 的 e fail 指针指向的是 ue 的 e， 同时 ue 的 e 指向的是 e 的 e。 好绕 0.0

后记：
字典树中使用 next[26] 来保存字符信息，有些浪费。如果关键字很稀疏的话，大部分的指针空闲，造成浪费。如果只用 node *next，char contant保存的话，每次查询的时候都需要遍历next，如果关键字很密集的话，时间开销过大

鸣谢带我入门的blog AC自动机算法