排序算法五—归并排序

1、归并思想——分治法

分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。

分治算法的一般步骤：

（1）分解，将要解决的问题划分成若干规模较小的同类问题；

（2）求解，当子问题划分得足够小时，用较简单的方法解决；

（3）合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。

归并排序是分治算法的典型应用。

2、归并排序基本思想

将待排序序列R[0...n-1]看成是n个长度为1的有序序列，将相邻的有序表成对归并，得到n/2个长度为2的有序表；将这些有序序列再次归并，得到n/4个长度为4的有序序列；如此反复进行下去，最后得到一个长度为n的有序序列。

综上可知：

归并排序其实要做两件事：

（1）“分解”——将序列每次折半划分。

（2）“合并”——将划分后的序列段两两合并后排序。

因此采用递归的方式。

//归并排序
public class mergeSort {
	//归并排序
	//将有序arr[start,mid]与有序arr[mid+1,end]进行归并排序，放入到brr[0,arr.length-1]中，然后再赋值给arr[start,end]
	public void merge(int[] arr,int[] brr,int start,int mid,int end){
		int i = start;
		int j = mid+1;
		int k = 0;
		//比较两个有序数组的元素，较小的放入到brr中
		while(i<=mid && j<=end){
			if(arr[i]<arr[j]){
				brr[k++] = arr[i++];
			}else {
				brr[k++] = arr[j++];
			}
		}
		//将剩余的部分放入brr中，
		//也许是arr[start,mid] 或者 arr[mid+1,end]
		while(i<=mid){
			brr[k++] = arr[i++];
		}
		while(j<=end){
			brr[k++] = arr[j++];
		}
		
		//将brr中的元素赋值给arr
		for(i = 0; i<k;i++){
			arr[i+start] = brr[i];
		}
	}
	
	//递归调用排序
	public void mSort(int[] arr,int[] brr,int start,int end){
		if(start<end){  //限制条件（容易忽略）
			int mid = (start+end)/2;
			mSort(arr,brr,start,mid); //左边递归排序
			mSort(arr, brr,mid+1, end);//右边递归排序
			merge(arr, brr, start, mid, end);//左右两边合并排序
		}
	}
	
	//测试调用mSort
	public static void main(String[] args){
		//排序数据
		int[] arr = {3,7,5,1,6,2,4};
		System.out.println("mergesort before:");
		for(int i = 0; i<arr.length;i++){
			System.out.print(arr[i]+",");
		}
		System.out.println("");
		int[] brr = new int[10];
		new mergeSort().mSort(arr,brr,0,arr.length-1);
		System.out.println("mergeSort after:");
		for(int i = 0; i<arr.length;i++){
			System.out.print(arr[i]+",");
		}
	}
	
	/*
	 * 归并排序的时间复杂度为 O(n*logn),但是需要额外的长度为n的辅助数组
	 * 占用额外空间是归并排序不足的地方，但是它是几个高效排序算法（快速排序、堆排序、希尔排序）中唯一稳定的排序方法。
	 * */
}

程序执行结果：

执行步骤：

先将初始数组分为两部分，先归并低位段，再归并高位段。对低位段与高位段继续分解，低位段分解为更细分的一对低位段与高位段，高位段同样分解为更细分的一对低位段与高位段，依次类推。

上例中，第一步，归并的是3与7，第二步归并的是5和1，第三部归并的是前两步归并好的子段[3,7]与[1,5]。至此，数组的左半部分（低位段）归并完毕，然后归并右半部分（高位段）。

所以第四步归并的是6与2，第四部归并的是4，第五步归并的是前两步归并好的字段[2,6]与[4]。至此，数组的右半部分归并完毕。

最后一步就是归并数组的左半部分[1,3,5,7]与右半部分[2,4,6]。

归并排序结束。

3、归并排序的特性

时间复杂度： O(N* log ₂ N)，空间复杂度：O(n) ，稳定性：是稳定的

先来分析一下复制的次数。

如果待排数组有8个元素，归并排序需要分3层，第一层有四个包含两个数据项的自数组，第二层包含两个包含四个数据项的子数组，第三层包含一个8个数据项的子数组。合并子数组的时候，每一层的所有元素都要经历一次复制（从原数组复制到workSpace数组），复制总次数为3*8=24次，即层数乘以元素总数。

设元素总数为N，则层数为log₂N，复制总次数为N*log₂N。

其实，除了从原数组复制到workSpace数组，还需要从workSpace数组复制到原数组，所以，最终的复制复制次数为2*N*log₂N。

在大O表示法中，常数可以忽略，所以归并排序的时间复杂度为O(N* log₂N)。

一般来讲，复制操作的时间消耗要远大于比较操作的时间消耗，时间复杂度是由复制次数主导的。

 

下面我们再来分析一下比较次数。

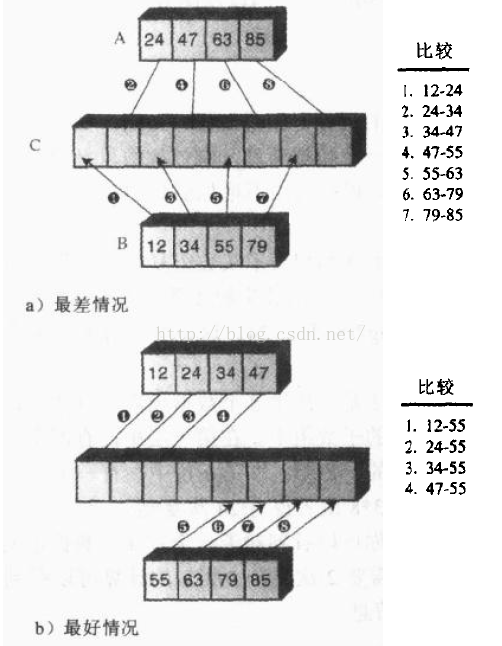
在归并排序中，比较次数总是比复制次数少一些。现在给定两个各有四个元素的子数组，首先来看一下最坏情况和最好情况下的比较次数为多少。

第一种情况，数据项大小交错，所以必须进行7次比较，第二种情况中，一个数组比另一个数组中的所有元素都要小，因此只需要4次比较。

当归并两个子数组时，如果元素总数为N，则最好情况下的比较次数为N/2，最坏情况下的比较次数为N-1。

假设待排数组的元素总数为N，则第一层需要N/2次归并，每次归并的元素总数为2；则第一层需要N/4次归并，每次归并的元素总数为4；则第一层需要N/8次归并，每次归并的元素总数为8……最后一次归并次数为1，归并的元素总数为N。总层数为log₂N。

最好情况下的比较总数为：

N/2*(2/2)+ N/4*(4/2)+N/8*(8/2)+...+1*(N/2) = (N/2)*log₂N

最好情况下的比较总数为：

N/2*(2-1)+ N/4*(4-1)+N/8*(8-1)+...+1*(N-1) =

(N-N/2)+ (N-N/4)+(N-N/8)+...+(N-1)=

N*log₂N-(1+N/2+N/4+..)< N*log₂N

可见，比较次数介于(N/2)*log₂N与N*log₂N之间。如果用大O表示法，时间复杂度也为O(N* log₂N)。