二叉搜索树（binary search tree）

定义

二叉搜索树：二叉树中任何节点的键值一定大于其左子树中每一个节点的键值，并且小于其右子树中每一个节点的键值。

查找

基于此，在二叉搜索树中搜索最小元素和最大元素是方便的，从根节点开始，一直往左走，直至无路可走，就得到了最小元素；从跟节点开始，一直往右走，直至无路可走，就得到了最大元素。
查找任何一个节点也是方便的。从跟节点开始，目标值比当前节点的键值大，就继续往右走，目标值比当前节点的键值小，就继续往左走。

插入

首先找到合适的位置。从跟节点开始，如果要插入的值比当前节点的键值大，则往右走；如果要插入的值比当前节点的键值小，就往左移动。直到无路可走就找到了插入节点的合适位置。新建一个节点、赋值、插入。

删除

1、要删除的节点没有子节点。直接删除即可。
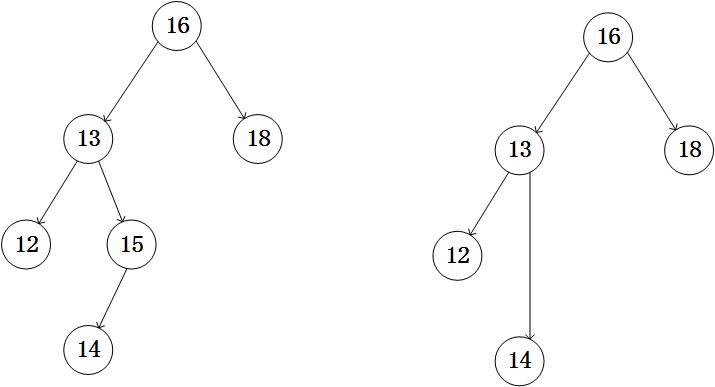
2、要删除的节点只有一个孩子节点。删除后直接将孩子节点连接上即可。例如要删除节点15，删除15后，14成为了13的右节点。

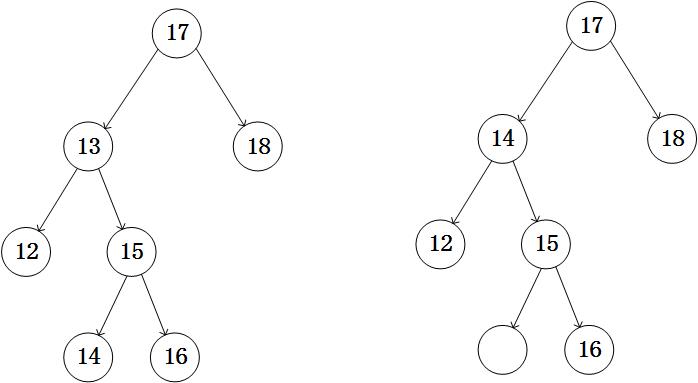
3、要删除的节点有两个孩子节点。将又子树的最小值替换要删除的节点。例如要删除节点13，用13的右子树中的最小值14替换掉13，然后删除14节点即可。