前两篇关于KMP算法的基础介绍:
http://blog.csdn.net/u011028771/article/details/52966473
http://blog.csdn.net/u011028771/article/details/52966977
前两篇博客分别介绍了KMP算法的理论基础及代码实现,但是KMP算法实现的核心在于next数组的求取,第一篇论文中介绍了next数组的手动求取方法;第二篇博客中介绍了代码实现,当时没有讲清楚,而且代码实现存在一定问题。本篇博文将详细介绍next数组的求取办法及代码实现。首先看下面的例子:
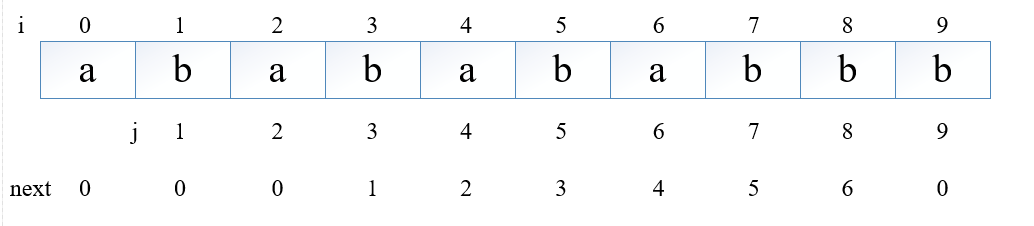
图中i从0开始,j从1开始;i小于j;
手动求next数组在第一篇博客中介绍过,结果如图所示。
接下来介绍计算机该如何实现(主要是第二篇博客中介绍的i的回溯问题):
1. i=0;j=1;T[i]!=T[j];next[2]=0;
二者不等表明:每一个位置的最大前缀和最大后缀不可能再相等了。所以比较次大前缀和后缀,因此将j加一。注意前提是i=0;
2. i=0;j=2;T[i]=T[j];next[3]=1;
此时,表明次大的前缀后缀是可以相等的;因此将二者同时加1;
3. i=1;j=3;T[i]=T[j];next[4]=2;同理:
4. i=2;j=4;T[i]=T[j];next[5]=3;同理:
5. i=3;j=5;T[i]=T[j];next[6]=4;同理:
6. i=4;j=6;T[i]=T[j];next[7]=5;同理:
7. i=5;j=7;T[i]=T[j];next[8]=6;同理:
8. i=6;j=8;T[i]!=T[j];
此时表明:次大的前后缀相等的情况到此为止;以后位置的次大前后追都不可能相等了。理论上此时需要考虑三级前后缀是否相等了;及i=5;j=8的情况;
但是需要注意,即使i=5与j=8位置相等了,那么接下来我们需要核实i=4与j=7位置是否相等,这样一来j和i都需要回溯;显然是复杂的,而且提升了运算复杂度;
那么我们考虑如何利用next来简化运算;首先i=7与j=8位置相等是没有意义的,第一步的时候已经验证最大前后缀不可能相等;i=6与i=8位置不相等。此时我们可以考虑i=6位置的最大相等的前后缀;这样就可以利用之前已经比较的成果了,减少i和j的回溯;那么,为什么是i=6位置的最大前后缀呢?已经讲过了,i=7;i=6;位置与j=8处均不相等或者没有意义,所以目前最大的前后缀只能是从i=6位置开始。
所以此次回溯是i=6;回溯到i=next[6]=4;
验证一下:
假设i=4位置与j=8位置相等;那么我们接下来需要判断:i=3,j=7;i=2,j=6;i=1,j=5;i=0,j=4;这些位置的情况吗?显然是不需要的;因为next[6]=4;意味着:i=0,j=2;i=1,j=3;i=2,j=4;i=3,j=5;是相等的。那么:因为i=0与j=2相等;i=2与j=4相等;则0,2,4位置上的字符一定是相等的;所以i=0与j=4是相等的,同理可以知道i=1与j=5也是相等的;接下来就剩下i=2,j=6;i=3,j=7;这两种情况,next[8]=6,next[7]=5都能推出。注意:i能走到6那么,i=4,i=5一定与i=3是连续的,否则i会在i=4或者i=5回溯;所以next[6]=4,则next[7]=5,next[8]=6是一定的,即i=2,j=6;i=3,j=7;相等是一定的。
i的回溯问题解决了,那么next数组的求取就十分简单了。
9. i=next[6]=4;j=8;T[i]!=T[j];回溯;
10. i=next[4]=2;j=8;T[i]!=T[j];回溯;
11. i=next[2]=0;j=8;T[i]!=T[j];
注意:此时虽然还不相等,但是i=0了;以第一步相同,i不变,j加一;
next[9]=0;
运算结束!!!
算法的求取方法介绍完了,直接上代码
int compNext(char *check, int *next, int sizeCheck) {
int j = 1;
int i = 0;
while (j < sizeCheck-1) {
if (check[i] == check[j]) {
i++;
j++;
next[j] = i;
}
else {
if (i == 0) {
j++;
next[j] = 0;
}
else
i=next[i];
}
}
for (i = 0; i < sizeCheck; i++) {
printf("%d", next[i]);
}
return OK;
}





















 2086
2086

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








