可持久化线段树

线段树想必大家都知道，是一种十分有用的数据结构。请看一道例题

题目：一堆数，有两种操作，1.将x这个位置改成y 2.查询x~y之间的最大值

很简单的一道题，现在将题目改变一下，变成

题目：一堆数，有两种操作，1.将x这个位置改成y 2.查询第T时刻x~y之间的最大值

那么有了T时刻后怎么做？
用可持久化线段树！（主席树）
很容易想到对于每个时刻开个线段树，不过不仅耗空间，而且耗时间。
那么有没有更好的方法呢？
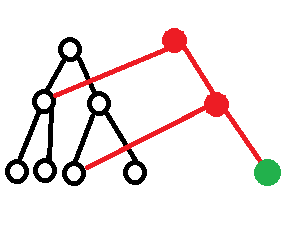
给一张图：

黑色的为原有的树，绿色为要修改的点，红色为新建的树。
对于不需要修改的区间，直接指向原有的点，需要修改的区间，建立新点并连过去。
那么这道题就可以迎刃而解了。
区间修改与单点修改一样。如果左右两个区间都要修改，就开两个新点即可。设一个lazy标记下传。
下传程序：

void down(int v,int i,int j)
{
    if (i==j) {tree[v].lazy=0;return;}
    int mid=(i+j)/2;
    tree[++tot]=tree[tree[v].l];tree[tot].data+=tree[v].lazy;tree[tot].lazy+=tree[v].lazy;tree[v].l=tot;
    tree[++tot]=tree[tree[v].r];tree[tot].data+=tree[v].lazy;tree[tot].lazy+=tree[v].lazy;tree[v].r=tot;
    tree[v].lazy=0;
}

这里可以看到如何开新点并连过去。

区间修改总程序：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define N 10100000
using namespace std;
struct note{
    int l,r,data,lazy;
};
note tree[N];
int n,a[N],g[N],tot=1,ans,tt=1;
void build(int v,int i,int j)
{
    if (i==j) {tree[v].data=a[i];return;}
    int mid=(i+j)/2;
    tree[v].l=++tot;build(tot,i,mid);
    tree[v].r=++tot;build(tot,mid+1,j);
    tree[v].data=max(tree[tree[v].l].data,tree[tree[v].r].data);
}
void down(int v,int i,int j)
{
    if (i==j) {tree[v].lazy=0;return;}
    int mid=(i+j)/2;
    tree[++tot]=tree[tree[v].l];tree[tot].data+=tree[v].lazy;tree[tot].lazy+=tree[v].lazy;tree[v].l=tot;
    tree[++tot]=tree[tree[v].r];tree[tot].data+=tree[v].lazy;tree[tot].lazy+=tree[v].lazy;tree[v].r=tot;
    tree[v].lazy=0;
}
void insert(int v,int i,int j,int x,int y,int z)
{
    if (i==x && j==y) {tree[v].data+=z;tree[v].lazy+=z;return;}
    int bz=0;
    if (tree[v].lazy) down(v,i,j),bz=1;
    int mid=(i+j)/2;
    if (y<=mid) 
    {
        if (!bz) tree[++tot]=tree[tree[v].l],tree[v].l=tot;
        insert(tree[v].l,i,mid,x,y,z);
    }
    else if (x>mid) 
         {
            if (!bz) tree[++tot]=tree[tree[v].r],tree[v].r=tot;
            insert(tree[v].r,mid+1,j,x,y,z);
         }
         else
         {
            if (!bz) tree[++tot]=tree[tree[v].l],tree[v].l=tot;insert(tree[v].l,i,mid,x,mid,z);
            if (!bz) tree[++tot]=tree[tree[v].r],tree[v].r=tot;insert(tree[v].r,mid+1,j,mid+1,y,z);
         }
    tree[v].data=max(tree[tree[v].l].data,tree[tree[v].r].data);
}
void find(int v,int i,int j,int x,int y)
{
    if (i==x && j==y) {ans=max(ans,tree[v].data);return;}
    if (tree[v].lazy) down(v,i,j);
    int mid=(i+j)/2;
    if (y<=mid) find(tree[v].l,i,mid,x,y);
    else if (x>mid) find(tree[v].r,mid+1,j,x,y);
         else find(tree[v].l,i,mid,x,mid),find(tree[v].r,mid+1,j,mid+1,y);
}
int main()
{
    freopen("chairmantree.in","r",stdin);
    freopen("chairmantree.out","w",stdout);
    scanf("%d",&n);
    g[1]=1;
    fo(i,1,n) scanf("%d",&a[i]);
    build(g[1],1,n);
    int ac;scanf("%d",&ac);
    for(;ac;ac--)
    {
        int x,y,z,yy;
        scanf("%d%d%d",&x,&y,&z);
        if (x==1) 
        {
            scanf("%d",&yy);
            g[++tt]=++tot;tree[tot]=tree[g[tt-1]];
            insert(g[tt],1,n,y,z,yy);
        }
        if (x==2)
        {
            ans=-2147483647;find(g[tt],1,n,y,z);
            printf("%d\n",ans);
        }
    }
}