NOTE：NEURAL NETWORKS

NEURAL NETWORKS

The note for reading chapters 5 of pattern recognition and machine learning .

提起机器学习的种种方法时，有两种算法大家都耳熟能详，一种叫做神经网络，一种叫做支持向量机（SVM）。本文主要是围绕神经网络来讨论，但在一开始，不得不提及一下SVM。在对SVM和神经网络学习的过程中，我认为二者存在某些特别的关联，即二者都是通过一种自反馈的方法去得到最终的答案。SVM本质上是解决一个凸函数的优化问题，对于这个凸函数，使用了迭代的方法进行求解，而在这个过程中，每一步迭代都在更新其权重，最后收敛，得到权重值。而神经网络也是相类似的，只是因为神经网络缺少SVM那样严密的数学基础，但因此神经网络可以解决非凸问题，并通过一些自反馈的机制去得到这个模型中需要的种种权重。下面让我们站在前人的肩膀上，一窥究竟

Feed-forward Network Function

首先，让我们来定义一个非线性的回归或者分类问题。
$y(x,w)=f(\sum_{j=1}^{M}w_j\Phi_j(x))$
其中$f(·)$表示一个非线性激励（activation）函数，$\Phi_j(x)$表示基函数。

接下来，介绍一下基本的神经网络模型，又称single-hidden-layer network，我们可以通过一系列的转换函数来描述。

• input：$x_1,x_2,x_3,...,x_D$
• weight: $w_{ij}^{(layer)}$
• biases: $w_{j0}^{(0)}$
• activations: $a_j=\sum_{i=1}^{D}w_{ji}^{(1)}x_i+w_{j0}^{(0)}$
• nonlinear activation function: $h(·)\rightarrow z_j=h(a_j)$
  一般为sigmoidal function，如logistic sigmoid，‘tanh’function,并且$z_j$表示神经网络中的中间输入
• output unit activations：$a_k=\sum_{j=1}^{M}w_{kj}^{(2)}z_j+w_{k0}^{(2)}$ K是输出变量的总数
• appropriate activation function：$\sigma(·)$
• outputs：$y_k=\sigma(a_k)$ where $\sigma(a)=\frac{1}{1+exp(-a)}$.

上面从input到output中间的叫做隐藏单元（hidden unit）。
把上面所有的结合起来，写成一个总公式就是：$y_k(x,w)=\sigma(\sum_{j=1}^{M}w_{kj}^{(2)}h(\sum_{i=1}^{D}w_{ji}^{(1)}x_i+w_{j0}^{(1)})+w_{k0}^{(2)})$这个式子被叫做前向传播。
当然，这里的神经网络模型层数非常少，这是因为经典的神经网络层数增加带来计算量的增加非常大。回到这个模型，如果将其画出来如下：

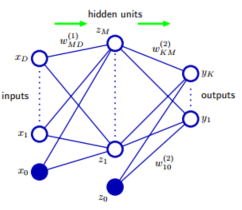
这个图与机器学习中的图模型是完全不同的，因为每一个节点不表示一个确定的变量，每一个连线也不具备概率等含义。
为了简化上面的公式，我们可认为$x_0=1$，从而将上式写为：$y_k(x,w)=\sigma(\sum_{j=0}^{M}w_{kj}^{(2)}h(\sum_{i=0}^{D}w_{ji}^{(1)}x_i))$这可以看成是集合了两层感知器模型，这也是为什么神经网络也被称为是多层感知器的缘由。所以其中$\sigma,h$两个激励函数的不同会得出不同的权重，这个是神经网络训练的一个重要的特征。
如果隐藏单元中的activation function是线性的，那么我们可以找到一个没有隐藏单元的网络与之等价。
如果隐藏单元的数量比输入或者输出变量的个数少，那么说明神经网络中transformation从输入到输出的变化不是最好的线性变换most general possible linear transform，因为在隐藏单元处发生降维，从而丢失了信息。

接下来，我们介绍一个同样一般的神经网络模型，其中包括skip-layer connection，如下图：

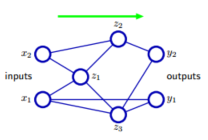
通常，选择一个足够小的第一层权重，可以使得single-hidden-layer network模仿skip-layer connection，在实际生成模型时，这是一个比较好的方法。这也从侧面说明了神经网络可以使稀疏的，因为前向传播的限制，产生的图一定是没有回路的，所以输入输出之间的函数是确定的，故，我们可以用下面的式子来表示神经网络中每一个单元的计算公式：
$z_k=h(\sum_jw_{kj}z_j)$
这里求和范围是之前与之相联的所有单元。

Weight-spase symmetries

神经网络模型和贝叶斯网络模型相比有一个特点，贝叶斯模型对于任何一个映射函数，其输入输出是确定的其图模型结构往往是通过某些特定的先验知识构造的，哪些节点之间有关系往往是确定的，而神经网络模型不同，两层之间往往是全连接的，如果两个节点之间没有关系，如上面所说的skip-layer connection，是通过权重值来体现的，这意味着神经网络是一个黑盒子，并不需要足够的先验知识去构造模型。
当我们使用’tanh’ function作为activation function的时候，如果我们改变某一个隐藏单元的所有参数（权重和偏差）的符号（+/-），那么由于’tanh’是奇函数，在整个神经网络中其从输入到输出的映射是不变的。所以存在两个不同的权重向量得到同一个神经网络模型。也就是说，对于一个有M个隐藏单元的神经网络，存在M个这样的（‘sign-flip’symmetries）正负等价，即对于任意给定的权重向量，存在$2^M$个等价的权重向量。

Network Training

前面我们讨论了神经网络的泛化模型，现在我们来看几个实际的例子。
以曲线拟合为例，讨论对于一个回归问题，给定的训练集，输入向量为${x_n}$，对应的目标向量为${t_n}$，最小化错误率函数:
$E(w)=\frac{1}{2}\sum_{n=1}^{N}\Arrowvert y(x_n,w)-t_n \Arrowvert ^2$
这里我们假设t符合高斯分布，同时t也是神经网络模型中的输出。
$p(t|x,w)=N(t|y(x,w),\beta ^{-1})$,这里$\beta$是高斯噪声。这里我们有足够的理由把这个式子看作是输出单元的激励函数，因为他可以表示任意从x映射到y的函数。对于理想的相互独立的观测变量$X=\{ x_1,x_2,...,x_N \}$，可以计算他的似然函数：
$p(t|X,w,\beta)=\prod _{n=1}^{N}p(t_n|x_n,w,\beta)$
求对数，得到其对数似然：
$\frac {\beta}{2}\sum _{n=1}^{N}\{y(x_n,w)-t_n\}^2-\frac{N}{2}In\beta+\frac{N}{2}In(2\pi)$
对数似然可以用来计算参数$w,\beta$。在神经网络模型中，我们计算的机理在于最小化误差函数，而不是最大似然，虽然二者在数学上可以看作是等价的。因为最大似然和最小二乘（形式跟对数似然几乎一样）是等价的,只不过丢弃了后面两个常量。
$E(w)=\frac {1}{2}\sum _{n=1}^{N}\{y(x_n,w)-t_n\}^2$
通过最小化$E(w)$我们可以求解得到$w_{ML}$，而在神经网络中，由于$y(x_n,w)$是非线性的，所以$E(w)$是非凸的函数，并且用神经网络求解，得到的一般是局部最优解。计算得到$w_{ML}$之后，我们就可以通过最小化对数似然去求解$\beta _{ML}$.
$\frac {1}{\beta _{ML}}=\frac{1}{NK}\sum_{n=1}^{N}\Arrowvert y(x_n,w_{ML})-t_n \Arrowvert ^2$
K是我们要求解的目标变量的数量。
在这个例子中，我们可以认为我们的输出激励函数是一个恒等式，即$y_k=a_k$，并且错误率函数满足下面的性质：
$\frac{\partial E}{\partial a_k}=y_k-t_k$
这个性质可以用于讨论错误率的后向传播。

前面我们举了一个回归问题的例子，下面我们来讨论一下分类问题。假设我们的分类问题非常简单，目标变量的取值只有0和1，其输出激励函数为logistic sigmoid函数：
$y=\sigma(a)\equiv \frac{1}{1+exp(-a)}$
$y(x,w)$可以看成是条件概率$p(C_1|x)$，对于给定的输入，目标变量符合Bernouli分布，考虑我们的训练集是独立观测得到的，我们的错误率函数的最大对数似然形式就是交叉熵错误率函数：
$E(w)=-\sum_{n=1}^{N}\{t_nIny_n+(1+t_n)In(1-y_n)\}$这里$y_n$就是$y(x_n,w)$.
如果分的类别不止两类，则对于给定的输入，目标变量满足的条件概率分布为：
$p(t|x，w)=\prod _{k=1}^{K}y_k(x,w)^{t_k}[1-y_k(x,w)]^{1-t_k}$
其错误率函数：
$E(w)=-\sum_{n=1}^{N} \sum_{k=1}^{K}\{t_{nk}Iny_{nk}+(1+t_{nk})In(1-y_{nk})\}$这里$y_{nk}$就是$y(x_{nk},w)$.
最终，我们的输出单元激励函数可以写成softmax函数：
$y_k(x,w)=\frac{exp(a_k(x,w))}{\sum_{j}exp(a_j(x,w))}$

Parameter optimization

在上面我们提到的求解权重向量w中，我们反复提到，可以通过最小化$E(w)$求解，这里我们来讨论参数的优化问题。下面是错误率函数的图形：

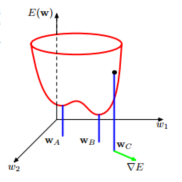
其中$w_A$是局部最优，$w_B$是全局最优，$w_C$表示任意一个点（我们求解是随机初始化的一个值），$\bigtriangledown E$是通过错误率函数表面得到的一个局部梯度。从这个图以及基于梯度的优化方法，我们可以很明确的知道，神经网络模型不一定能得出全局最优解。

Error Backpropagation

前面我们主要讨论了前向传播的神经网络模型，这种神经网络模型的思想脱胎于感知机，不同的是，前向传播神经网络模型是多层的，而我们所说的感知机通常是单层的。在前向传播神经网络模型中，信息主要是一层一层的往前传播，信息既然可以往前传播，自然也可以向后传播，这里我们将这样的神经网络模型称为error backpropagation。向后传播信息的引入使得神经网络模型成为了完全不同的东西，尽管后向传播也使用了多层感知机和基于最小二乘错误率函数的梯度下降求解参数的思想。
绝大多数的训练算法都涉及利用迭代求解最小化错误率函数并且在每一步中调整参数。我们可以将其分成两步：第一步，对错误率函数关于权重参数求微分；第二步，利用求得的微分调整权重参数。
从这两步中，我们可以看出来向后传播算法一个重要的基础是具有一个有效可计算的方式去计算错误率函数关于权重参数的微分。通过这样的微分，我们可以在神经网络中向后传播当前参数好坏的信息。

Evaluation of error-function derivation

现在我们讨论一般框架下的后向传播算法，假设神经网络的前馈结构是任意给定的，激励函数也是任意非线性可微的，错误率函数的形式也是广泛的。神经网络模型是single-hidden-layer，并且可以用平方和来刻画错误程度。
在一般的前向网络中，每一个单元值等于输入的和：
$a_j=\sum_iw_{ji}z_i$(a)
$z_i$是j单元的activation，或者叫输入，而$z_i$是通过一个非线性函数转换而来的，即$z_j=h(a_j)$(b),可以把$z_j$看成是这个j单元的输出。
由于我们是对错误率函数关于权重参数求微分，很显然，这里面的计算只与$w_{ji}$有关，但是我们可以通过微分的链式法则引入$a_j$:
$\frac{\partial E_n}{\partial w_{ji}}=\frac{\partial E_n}{\partial a_{j}}\frac{\partial a_j}{\partial w_{ji}}$令，$\delta _j \equiv \frac{\partial E_n}{\partial a_{j}} 并且 \frac{\partial a_j}{\partial w_{ji}}=z_i$通常我们把$\delta$叫做errors.
带入得到：$\frac{\partial E_n}{\partial w_{ji}}=\delta _j z_i$.
当向前计算得到$y_k$时，因为训练数据中给出了$t_k$可以计算出$\delta_k$.由微分的链式法则，可以推算中间隐藏单元的$\delta_j$:
$\delta _j \equiv \frac{\partial E_n}{\partial a_{j}} =\sum_k\frac{\partial E_n}{\partial a_{k}}\frac{\partial a_k}{\partial a_{j}}$
把上面的(a)(b)两个式子带入，可以得到：
$\delta_j=h^,(a_j)\sum_kw_{kj}\delta_k$
我们可以将Error Backpropagation的算法流程总结如下：

1. 对输入$x_n$用前向传播的方法求解得到所有的隐藏单元值和输出单元值
2. 通过利用输出单元值计算$\delta_k$
3. 通过后向传播计算每一个隐藏单元的$\delta$值
4. 用$\frac{\partial E_n}{\partial w_{ji}}=\delta _j z_i$计算需要求解的微分值

如果有理解不对的地方，欢迎指正！