图的深度优先查找（DFS: Depth -First Search） （1）问题分析 DFS可从任意一个顶点开始访问，其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个顶点只能访问

 图的深度优先查找（DFS: Depth -FirstSearch）

（1）问题分析

DFS可从任意一个顶点开始访问，其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个顶点只能访问一次。

当从一个顶点无法深入访问时，这个顶点称为死端。在死端上，DFS沿来路后退一条边，到上一个顶点，尝试继续访问。

当后退到起始顶点并且起始顶点也是一个死端时，该算法停止。

如果仍有未访问顶点，算法从其中任一顶点开始，重复上述过程。

（2）解题思路

l  用栈记录DFS的遍历顺序

在第一次访问一个顶点的时候，将其入栈；当它成为一个死端的时候，将其出栈。

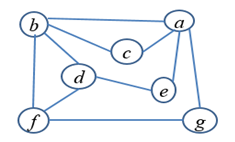
例：从顶点a开始用DFS算法遍历下图，按字母顺序选择未访问顶点。

过程：请参照课件

l  也可用深度优先查找森林表示DFS遍历顺序

遍历的初始顶点作为该森林中第一棵树的根。

任何一个顶点第一次从哪个顶点被访问到，就将其作为哪个顶点的子女。

连接这样两个顶点的边称为树向边。所有这种边构成一个森林。

从一个顶点向下一个顶点访问时，可能会遇到一条指向已访问顶点的边，并且这个顶点不是它的父母，这种边称为回边。

代码实现：

#include <iostream>
#include <cstring>
#define MAX(a,b) (a)>(b)?(a):(b)
#define MIN(a,b) (a)<(b)?(a):(b)
using namespace std;

int map[30][30];
int tof[30];
int maxn = -1, minn = 30;

// 从第a点搜索，a为路线中的第b个点
void DFS(int a, int b)
{
    int i;

    // 如果a没有被遍历过，则输出a点
    if (!tof[a]) return ;
    else tof[a] = 0;
    for (i = 0; i < b; ++i)
        printf("   ");
    printf("%c\n", a + 'a');

    // 继续搜索
    for (i = 0; i <= maxn; ++i)
        if (map[a][i])
            DFS(i, b + 1);
}

int main()
{
    int n, m;
    char a, b;
    int c, d;
    int i;

    // 输入
    memset(map, 0, sizeof(map));
    memset(tof, 0, sizeof(tof));
    printf("请输入顶点个数n以及边数m,格式为<n m>:");
    cin >> n >> m;
    printf("请分别输入%d条边所对应的两个顶点,格式为<a b>:\n",m);
    for (i = 0; i < m; ++i)
    {
        cin >> a >> b;
        c = a - 'a';
        d = b - 'a';
        tof[c] = tof[d] = 1;
        // 构建邻接矩阵，求出最小点和最大点
        map[c][d] = map[d][c] = 1;
        maxn = MAX(maxn, c);
        maxn = MAX(maxn, d);
        minn = MIN(minn, c);
        minn = MIN(minn, d);
    }
    // 进行深度优先搜索
    printf("深度优先生成树为：\n");
    for (i = minn; i <= maxn; ++i)
        if (tof[i])
            DFS(i, 0);
    printf("遍历结束!\n");
}

画如下所示的图：

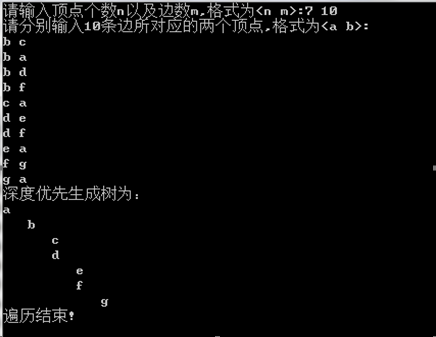
运行结果：

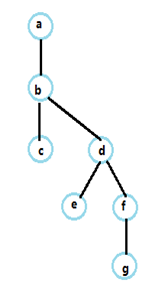
所形成的生成树为：