hdu-1077-Catching Fish-计算几何、枚举圆心

Link： http://acm.hdu.edu.cn/showproblem.php?pid=1077

Catching Fish

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 1731    Accepted Submission(s): 682

Problem Description

  Ignatius likes catching fish very much. He has a fishnet whose shape is a circle of radius one. Now he is about to use his fishnet to catch fish. All the fish are in the lake, and we assume all the fish will not move when Ignatius catching them. Now Ignatius wants to know how many fish he can catch by using his fishnet once. We assume that the fish can be regard as a point. So now the problem is how many points can be enclosed by a circle of radius one.

  Note: If a fish is just on the border of the fishnet, it is also caught by Ignatius.

Input

  The input contains several test cases. The first line of the input is a single integer T which is the number of test cases. T test cases follow.
  Each test case starts with a positive integer N(1<=N<=300) which indicate the number of fish in the lake. Then N lines follow. Each line contains two floating-point number X and Y (0.0<=X,Y<=10.0). You may assume no two fish will at the same point, and no two fish are closer than 0.0001, no two fish in a test case are approximately at a distance of 2.0. In other words, if the distance between the fish and the centre of the fishnet is smaller 1.0001, we say the fish is also caught.

Output

For each test case, you should output the maximum number of fish Ignatius can catch by using his fishnet once.

Sample Input

4
3
6.47634 7.69628
5.16828 4.79915
6.69533 6.20378
6
7.15296 4.08328
6.50827 2.69466
5.91219 3.86661
5.29853 4.16097
6.10838 3.46039
6.34060 2.41599
8
7.90650 4.01746
4.10998 4.18354
4.67289 4.01887
6.33885 4.28388
4.98106 3.82728
5.12379 5.16473
7.84664 4.67693
4.02776 3.87990
20
6.65128 5.47490
6.42743 6.26189
6.35864 4.61611
6.59020 4.54228
4.43967 5.70059
4.38226 5.70536
5.50755 6.18163
7.41971 6.13668
6.71936 3.04496
5.61832 4.23857
5.99424 4.29328
5.60961 4.32998
6.82242 5.79683
5.44693 3.82724
6.70906 3.65736
7.89087 5.68000
6.23300 4.59530
5.92401 4.92329
6.24168 3.81389
6.22671 3.62210

Sample Output

2
5
5
11

Author

  Ignatius.L

Recommend

  We have carefully selected several similar problems for you:  1056 1079 1099 1066 1849 

解释

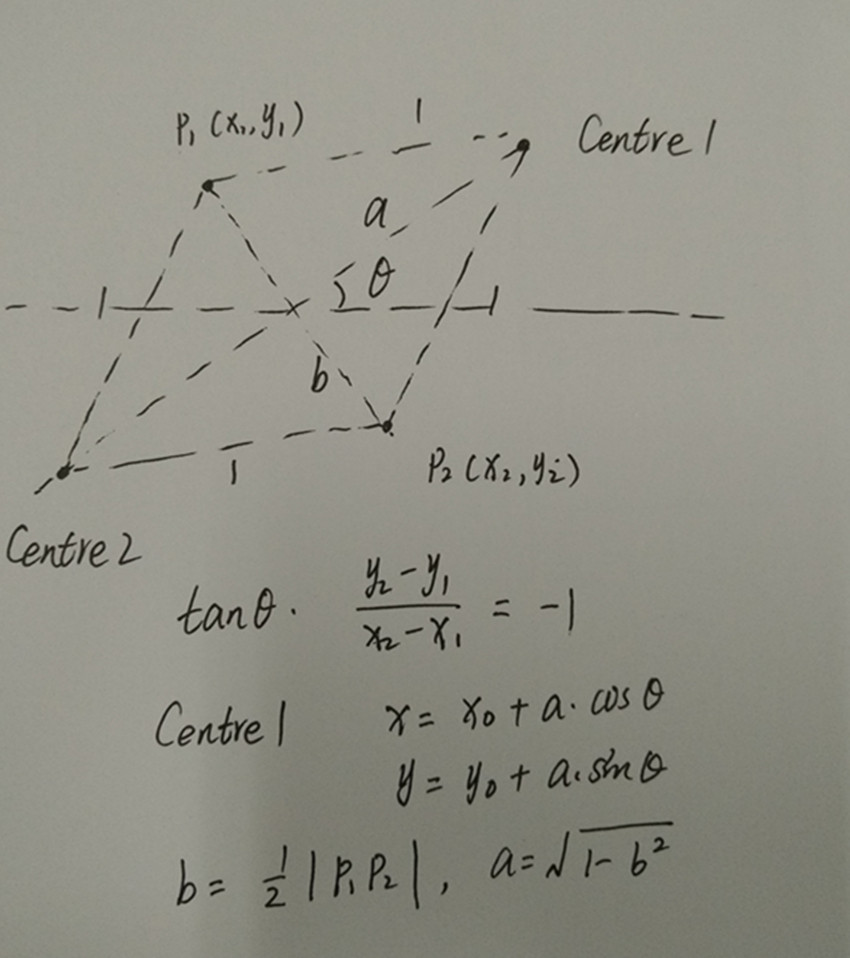
    简单计算几何，枚举圆心，然后计算最大值，不知道为什么一开始使用结构体超时，所以建议是尽量少使用结构体，多使用数组。

Code

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn(305);
int n;
int ans;
double poision[maxn][2];
double centre1[2],centre2[2];
void GetCentre(double a[],double b[])
{
    double x0=(a[0]+b[0])/2;
    double y0=(a[1]+b[1])/2;
    double h=sqrt(1-((a[0]-b[0])*(a[0]-b[0])+(a[1]-b[1])*(a[1]-b[1]))/4);
    if(fabs(a[1]-b[1])<1e-6)
    {
        centre1[0]=centre2[0]=x0;
        centre1[1]=y0+h;
        centre2[1]=y0-h;
    }
    else
    {
        double angel=atan((b[0]-a[0])/(a[1]-b[1]));
        centre1[0]=x0+h*cos(angel);
        centre1[1]=y0+h*sin(angel);
        centre2[0]=x0-h*cos(angel);
        centre2[0]=y0-h*sin(angel);
    }
}
int CatchFish()
{
    int res1=0;
    int res2=0;
    for(int i=0;i<n;i++)
    {
        if((centre1[0]-poision[i][0])*(centre1[0]-poision[i][0])+(centre1[1]-poision[i][1])*(centre1[1]-poision[i][1])<1.0001)
        {
            res1++;
        }
        if((centre2[0]-poision[i][0])*(centre2[0]-poision[i][0])+(centre2[1]-poision[i][1])*(centre2[1]-poision[i][1])<1.0001)
        {
            res2++;
        }
    }
    return max(res1,res2);
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int ans=1;
        scanf("%d",&n);
        for(int i=0;i<n;i++)
        {
            scanf("%lf%lf",poision[i],poision[i]+1);
        }
        for(int i=0;i<n;i++)
        {
            for(int j=i+1;j<n;j++)
            {
                GetCentre(poision[i],poision[j]);
                ans=max(ans,CatchFish());
            }
        }
        cout<<ans<<endl;
    }
}