讲一点有技术含量的东西（三）

讲一点有技术含量的东西（三）

    上次讲到，人耳对于不同频率的感觉不是一个线性关系，能否感觉出差别是取决于最小可感觉差，以下摘自维基百科 ：

    对许多感受维度而言，最小可觉差为一个随原始输入增减的函数，最小可觉差与原始刺激的比值则约略为常数。若以物理单位表达，可写为：

    是原始的刺激强度，则为在这个强度下所能感受到的最小变化量（也就是在此强度下的最小可觉差），k则是一个常数。此定律最早由Ernst Heinrich Weber（英语：Ernst Heinrich Weber），在进行“举重感知界限实验”时发现。由于理论比值（尚存有争议）之后被古斯塔夫·费希纳提出，因此这个定理常被称为韦伯-费希纳定理；至于常数k则称为Weber constant。这个定理对于大部分的感官维度都适用，至少有不错的近似值，如对于光线的强度，或者是对声音的强度及音高。不过也存在例外，如对光的波长的感知能力。

  最小可觉差是一个统计值（带有统计偏差）而非一标准值，在每次的试验中，对于同一个人的最小可觉差所得到的结果必定会有所浮动，因此要得到此值必须用大量的实验来决定界限。通常我们用一个人在50%的试验中能达到的辨识水准来表示此值，若使用其他比例，则通常会在形容时一并列出，如：75%最小可觉差。

    下面来说说平时所听到的音调，也就是1234567实际上对人耳会有什么样的影响。人耳是一个很精密的部件，恰如其分的屏蔽掉了不需要的声音，却又加强了需要获取关键信息时候的声音，譬如语音。人们对于频率的感知不是一个线性的关系，所以出线了1234567这个容易理解的线性音调，人们对于低频感知很强，对高频感知就没那么强烈，通俗的来说就是在同样的声压级下，1带给人的感受要比7更强烈。

    这中间的换算，需要一个梅尔系数。

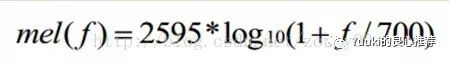
    如果你做语音识别，那么对这个一定会非常熟悉。在这还是说对于耳机的影响，如何从瀑布图和频响图上来看一个耳机是否对于人耳有足够的吸引力。首先来看一下频率图和梅尔系数图和换算关系。再来看一下实际应用时，真正对耳朵的影响。

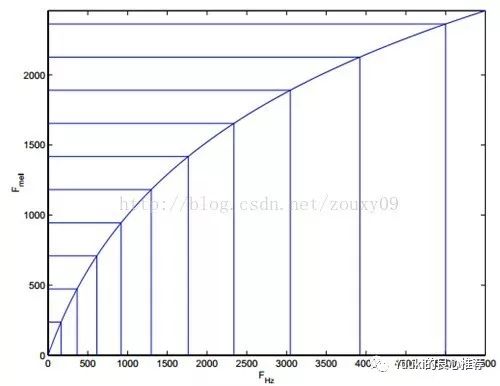
    看过这篇文章之后，再回头看第二篇文章，就会理解为什么很多HIFI厂商的产品到2K之后曲线不在平滑，不是做不到平滑，实际上是为了节约成本，在你感受不强烈的地方偷工减料，在低频1K的地方感受度是非常强的，所以三角滤波器会有很多，而到了高频，感受没那么明显所以三角滤波器只有几个，重叠的部分也更多。

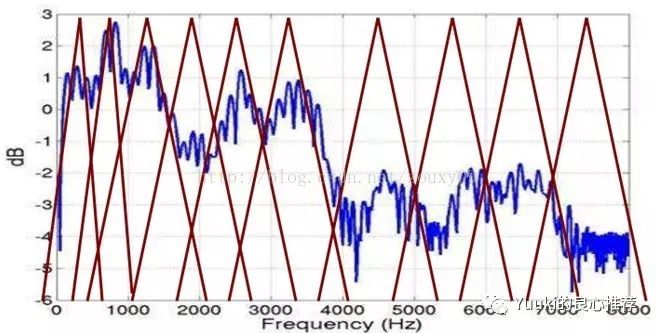
    下一次会说说MP3格式和无损格式，同样是在一般人不在意的地方偷工减料，不是说这样不好，其实如果没有抓住重点，没有找到人们的痛点，这样的产品是失败的，好的产品是又便宜又能解决核心问题，并不是面面俱到，一方面是为了做产品的区分有贵的便宜的，另一方面对于忽悠人来说有更多的素材可以讲。