遍历二叉树

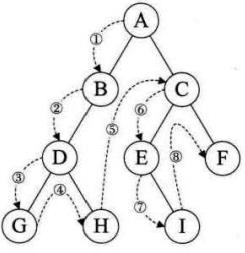
二叉树的遍历是指从根结点开始，按照某种次序依次访问二叉树中的所有结点，每个结点只能被访问一次。

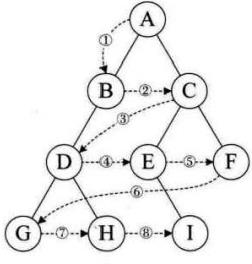
遍历的意义在于 把树中的结点变成某种有意义的线性序列。

前序遍历：

算法思想：

二叉树为空，则操作返回

不为空，则

       • 访问结点数据，并打印出来

        • 先序遍历左子树

        • 后序遍历右子树

实现代码：

void pre_order_travelse(btree_node* root)
{
 if(root != NULL)
 {
  printf("%c-", ((struct node*)root)->v);
  pre_order_travelse(root->left);
  pre_order_travelse(root->right);
 }
}

遍历效果：

中序遍历：

算法思想：

二叉树为空，则操作返回

不为空，则

        •  先序遍历左子树

       • 再访问结点数据，并打印出来

        • 后序遍历右子树

实现代码：

void mid_order_travelse(btree_node* root)
{
 if(root != NULL)
 {
  mid_order_travelse(root->left);
 
  printf("%c-", ((struct node*)root)->v);
 
  mid_order_travelse(root->right);
 }
}

遍历效果：

后序遍历：

算法思想：

二叉树为空，则操作返回

不为空，则

        •  先序遍历左子树

       • 后序遍历右子树

       • 最后访问结点数据，并打印出来

实现代码：

void post_order_travelse(btree_node* root)
{
 if(root != NULL)
 {
  post_order_travelse(root->left);
 
  post_order_travelse(root->right);
 
  printf("%c-", ((struct node*)root)->v);
 
 
 }
}

遍历效果：

层序遍历：

算法思想：

巧妙地利用了队列 FIFO 的思想

    • 访问根结点的数据

    • 访问第二层所有结点的数据

    • 访问第三层所有结点的数据

...

实现代码：

void level_order_travelse(btree_node* root)
{
 
 if(root != NULL)
 {
  LinkQueue* queue = LinkQueue_Create();
 
  if(queue != NULL)
  {
   
   LinkQueue_Append(queue, root);
   
   while( LinkQueue_Length(queue) > 0)
   {
    struct node* node = (struct node*)LinkQueue_Retrieve(queue);
   
    printf("%c, ", node->v);
   
    LinkQueue_Append(queue, node->header.left);
    LinkQueue_Append(queue, node->header.right);
   
   }
 
  }
 
  LinkQueue_Destroy(queue);
 }

}

遍历效果：

拓展：

关于队列在遍历中的使用还会用到，譬如图的广度优先遍历（BFS）