reference:http://blog.csdn.net/hjimce/article/details/50458190
一、相关理论
本篇博文主要讲解2014年ICLR的一篇非常牛逼的paper:《Network In Network》,过去一年已经有了好几百的引用量,这篇paper改进了传统的CNN网络,采用了少量的参数就松松击败了Alexnet网络,Alexnet网络参数大小是230M,采用这篇paper的算法才29M,减小了将近10倍啊。这篇paper提出的网络结构,是对传统CNN网络的一种改进(这种文献少之又少,所以感觉很有必要学习)。
传统的卷积神经网络一般来说是由:线性卷积层、池化层、全连接层堆叠起来的网络。卷积层通过线性滤波器进行线性卷积运算,然后在接个非线性激活函数,最终生成特征图。以Relu激活函数为例,特征图的计算公式为:
其中(i,j)表示图片像素点的位置索引,xij表示我们卷积窗口中的图片块,k则表示我们要提取的特征图的索引。
一般来说,如果我们要提取的一些潜在的特征是线性可分的话,那么对于线性的卷积运算来说这是足够了。然而一般来说我们所要提取的特征一般是高度非线性的。在传统的CNN中,也许我们可以用超完备的滤波器,来提取各种潜在的特征。比如我们要提取某个特征,于是我就用了一大堆的滤波器,把所有可能的提取出来,这样就可以把我想要提取的特征也覆盖到,然而这样存在一个缺点,那就是网络太恐怖了,参数太多了。
我们知道CNN高层特征其实是低层特征通过某种运算的组合。于是作者就根据这个想法,提出在每个局部感受野中进行更加复杂的运算,提出了对卷积层的改进算法:MLP卷积层。另一方面,传统的CNN最后一层都是全连接层,参数个数非常之多,容易引起过拟合(如Alexnet),一个CNN模型,大部分的参数都被全连接层给占用了,故这篇paper提出采用了:全局均值池化,替代全连接层。因此后面主要从这两个创新点进行讲解。
二、MLP卷积层(文献创新点1)
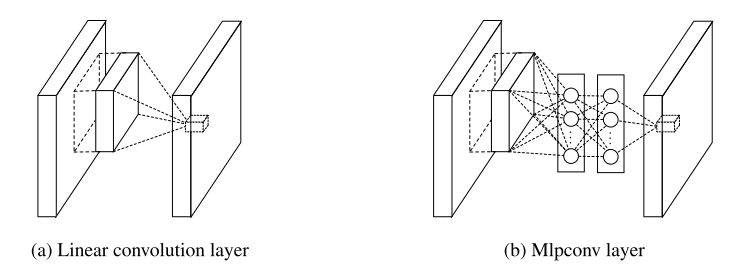
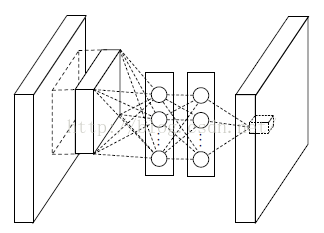
这个是文献的大创新点,也就是提出了mlpconv层。Mlpconv层可以看成是每个卷积的局部感受野中还包含了一个微型的多层网络。其实在以前的卷积层中,我们局部感受野窗口的运算,可以理解为一个单层的网络,如下图所示:
线性卷积层
CNN层的计算公式如下:
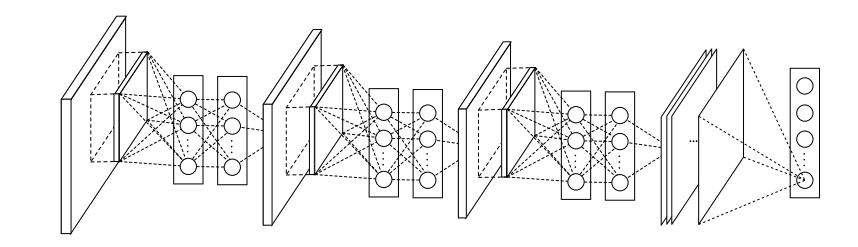
然而现在不同了,我们要采用多层的网络,提高非线性,于是mlpconv层的网络结构图如下::
Mlpconv层
从上面的图可以看到,说的简单一点呢,利用多层mlp的微型网络,对每个局部感受野的神经元进行更加复杂的运算.
而以前的卷积层,局部感受野的运算仅仅只是一个单层的神经网络罢了。对于mlpconv层每张特征图的计算公式如下:
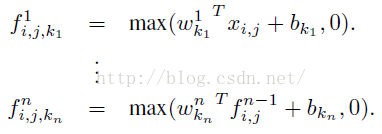
- <span style="font-size:18px;">layers {
- bottom: "data"
- top: "conv1"
- name: "conv1"
- type: CONVOLUTION
- blobs_lr: 1
- blobs_lr: 2
- weight_decay: 1
- weight_decay: 0
- convolution_param {
- num_output: 96
- kernel_size: 11
- stride: 4
- weight_filler {
- type: "gaussian"
- mean: 0
- std: 0.01
- }
- bias_filler {
- type: "constant"
- value: 0
- }
- }
- }
- layers {
- bottom: "conv1"
- top: "conv1"
- name: "relu0"
- type: RELU
- }
- layers {
- bottom: "conv1"
- top: "cccp1"
- name: "cccp1"
- type: CONVOLUTION
- blobs_lr: 1
- blobs_lr: 2
- weight_decay: 1
- weight_decay: 0
- convolution_param {
- num_output: 96
- kernel_size: 1
- stride: 1
- weight_filler {
- type: "gaussian"
- mean: 0
- std: 0.05
- }
- bias_filler {
- type: "constant"
- value: 0
- }
- }
- }
- layers {
- bottom: "cccp1"
- top: "cccp1"
- name: "relu1"
- type: RELU
- }
- layers {
- bottom: "cccp1"
- top: "cccp2"
- name: "cccp2"
- type: CONVOLUTION
- blobs_lr: 1
- blobs_lr: 2
- weight_decay: 1
- weight_decay: 0
- convolution_param {
- num_output: 96
- kernel_size: 1
- stride: 1
- weight_filler {
- type: "gaussian"
- mean: 0
- std: 0.05
- }
- bias_filler {
- type: "constant"
- value: 0
- }
- }
- }
- layers {
- bottom: "cccp2"
- top: "cccp2"
- name: "relu2"
- type: RELU
- }
- </span>
传统的卷积神经网络卷积运算一般是出现在低层网络。对于分类问题,最后一个卷积层的特征图通过量化然后与全连接层连接,最后在接一个softmax逻辑回归分类层。这种网络结构,使得卷积层和传统的神经网络层连接在一起。我们可以把卷积层看做是特征提取器,然后得到的特征再用传统的神经网络进行分类。
然而,全连接层因为参数个数太多,往往容易出现过拟合的现象,导致网络的泛化能力不尽人意。于是Hinton采用了Dropout的方法,来提高网络的泛化能力。
本文提出采用全局均值池化的方法,替代传统CNN中的全连接层。与传统的全连接层不同,我们对每个特征图一整张图片进行全局均值池化,这样每张特征图都可以得到一个输出。这样采用均值池化,连参数都省了,可以大大减小网络,避免过拟合,另一方面它有一个特点,每张特征图相当于一个输出特征,然后这个特征就表示了我们输出类的特征。这样如果我们在做1000个分类任务的时候,我们网络在设计的时候,最后一层的特征图个数就要选择1000,下面是《Network In Network》网络的源码,倒数一层的网络相关参数:
- layers {
- bottom: "cccp7"
- top: "cccp8"
- name: "cccp8-1024"
- type: CONVOLUTION
- blobs_lr: 1
- blobs_lr: 2
- weight_decay: 1
- weight_decay: 0
- convolution_param {
- num_output: 1000
- kernel_size: 1
- stride: 1
- weight_filler {
- type: "gaussian"
- mean: 0
- std: 0.01
- }
- bias_filler {
- type: "constant"
- value: 0
- }
- }
- }
全局均值池化层的相关参数如下:
- layers {
- bottom: "cccp8"
- top: "pool4"
- name: "pool4"
- type: POOLING
- pooling_param {
- pool: AVE
- kernel_size: 6
- stride: 1
- }
- }
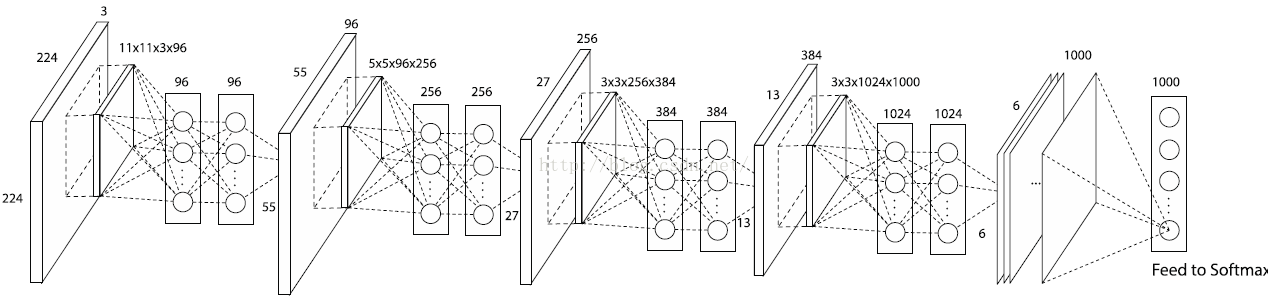
因为在Alexnet网络中,最后一个卷积层输出的特征图大小刚好是6*6,所以我们pooling的大小选择6,方法选择:AVE。
四、总体网络架构
根据上面的作者对传统CNN的两个改进,利用其进行1000物体分类问题,于是作者最后设计了一个:4层的NIN+全局均值池化,网络如下:
个人总结:个人感觉这篇文献很有价值,实现方式也很简单,一开始我还以为需要caffe的c++源码来实现NIN网络,结果发现实现NIN的源码实现方式其实就是一个1*1的卷积核,实现卷积运算,所以实现起来相当容易,不需要自己写源码,只需要简简单单的把卷积核的大小变一下,然后最后一层的全连接层直接用avg pooling替换一下就ok了。个人评价:网络浅显易懂,简单实现,却可以改进原来的网络,提高精度,减小模型大小,所以是一篇很值得学习的文献。后续即将讲解另外几篇2015年,也是对CNN网络结构改进的牛逼文献:《Spatial Transformer Networks》、《Striving For Simplicity:The All Convolutional Net》、《Stacked What-Where Auto-encoders》.
总结:
经典CNN中的卷积层其实就是用线性滤波器对图像进行内积运算,在每个局部输出后面跟着一个非线性的激活函数,最终得到的叫作特征图。而这种卷积滤波器是一种广义线性模型。所以用CNN进行特征提取时,其实就隐含地假设了特征是线性可分的,可实际问题往往是难以线性可分的。
GLM:(Generalized linear model)广义线性模型
GLM的抽象能力是比较低水平的,自然而然地我们想到用一种抽象能力更强的模型去替换它,从而提升传统CNN的表达能力。
抽象:指得到对同一概念的不同变体保持不变的特征。
什么样的模型抽象水平更高呢?当然是比线性模型更有表达能力的非线性函数近似器了(比如MLP,径向基神经)。
MLP的优点:
- 非常有效的通用函数近似器
- 可用BP算法训练,可以完美地融合进CNN
- 其本身也是一种深度模型,可以特征再利用
(MLP中的激活函数采用的是整流线性单元(即ReLU:max(wx+b,0))
采用了NIN改进CNN后,我们增强了局部模型的表达能力,这样我们可以在分类层对特征图进行全局平均池化,这种方式更有意义和容易解释(可将最后一层输出的特征图的空间平均值解释为相应类别的置信度!为什么可以这样解释呢?因为在采用了微神经网络后,让局部模型有更强的抽象能力,从而让全局平均池化能具有特征图与类别之间的一致性!),同时相比传统CNN采用的全连接层,不易过拟合(因为全局平均池化本身就是一种结构性的规则项)(PS:经典CNN容易过拟合,并严重依赖用dropout进行规则化)。
全局平均池化的优势:
- 通过加强特征图与类别的一致性,让卷积结构更简单
- 不需要进行参数优化,所以这一层可以避免过拟合
- 它对空间信息进行了求和,因而对输入的空间变换更具有稳定性
经典CNN为了解决广义线性模型抽象能力不足的问题,采用了过完备的滤波器集合来补偿,也就是说学习不同的滤波器用来检查同一特征的不同变体。但是过多的滤波器会对下一层施加额外的负担,因为下一层要考虑来自前一层所有的特征变体的组合。
为什么采用NIN是有价值的?
因为高层的特征(PS:论文中使用concept一词)来自低层特征的组合,在低层特征组合成高层特征之前,对每一局部块进行更好地抽象是有利的。
论文对比了maxout network,这种网络通过对仿射特征图进行最大值池化降低了输出特征图的数量。
仿射特征图(affine feature maps):是直接由线性卷积得到的特征图,没有通过激活函数进行非线性映射。
对线性函数进行最大化处理可得到分段线性函数近似器,可近似任意的凸函数!相比传统的CNN,maxout network更有效,因为可以区别凸集内的特征。但是maxout network是假设特征位于凸集中,这在实际中并不是总能满足的。
参考文献:
1、《Network In Network》
2、https://github.com/BVLC/caffe/wiki/Model-Zoo
3、https://gist.github.com/mavenlin/d802a5849de39225bcc6
4、《Maxout Networks》










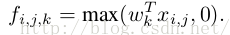
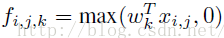















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








