这几天真是愁死我了~~~唉!废话少说,先整理下思路吧:
先说一句“积的取余 = 取余的积的取余”,后面也许会用得到。
1.我的想法开始于两个数相乘取余。
27*45 % 7=1215%7=4。
27*45%7=(3 * 7+6)*45 %7=(3*7*45+6*45)% 7=[ 3*7*45+6*(6*7+3)] % 7=(3*7*45+6*6*7+6*3) % 7=
6*3%7=4
于是,有了下面的程序:
运行结果:
上面的结果:1.正确且用时也很短很短 2.正确,但用时大约37秒 3.结果不对,且用时37秒。
将上面的类型改成__int64,也不对,结果是错误的。
2.学长给了提示,看一下“快速幂”
快速幂,就是平方 平方 地拆开,如 2^100=(2^50)^2=((2^25)^2)^2=((2^24*2)^2)^2=(((2^12)^2*2)^2)^2=......一直到指数为1,((2^1)^2)......当然要注意一下指数的奇偶:
k ^ m mod c = (a ^ 2) ^ (b / 2) mod c(b为偶);
k ^ m mod c = ((a ^ 2) ^ (b / 2) * a) mod c(b为奇数)。
算法如下:
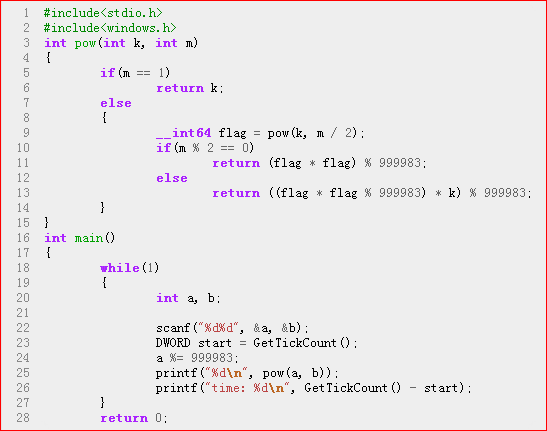
将上面程序改成取余的:
对于大数,结果不对。下面是学长的程序:
仔细分析下,我的原理跟他的差不多,以3,9,7,为例,我的是:
{[(3*3%7)*(3*3%7)%7]*[(3*3%7)*(3*3%7)%7]%7}%7*1*3%7
他的是把3换成了(3%7),数,比我的还小一些。但是,为什么,他的就可以算出结果,我的结果就不对呢?需注意一下:__int64 flag,类型!!!
结果正确,且运行时间很快。至于加不加“k%=m”,都无所谓了,能实现跟上面程序一样的功能。





























 2647
2647

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








