K-SVD是一个用于稀疏表示的字典学习算法,是一个迭代算法,是K-Means算法的泛化。
对于问题(1)
K-SVD的算法流程如下:
I)固定字典
,利用追踪算法(Pursuit Algorithm)求得(近似)最优的系数矩阵
;
II)每次更新一个列
(用SVD求解),固定字典
的其它所有的列。计算新的列
及其相对应系数,使得问题(1)最小化;
III)重复I)、II)直至收敛。
接下来我们会详细的讨论K-SVD算法:
在稀疏编码阶段,固定字典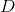
那么问题(1)可以被分解为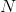
这个问题可以用OMP、BP、FOCUSS等追踪算法(Pursuit Algorithm)算法求解(这也体现了K-SVD算法的灵活性;FOCUSS能够得到更好地解,但OMP在保证比较好的解的同时,效率更高),并且如果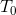
第二阶段(更新字典的列)会稍微复杂一点,假设固定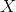
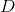
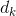
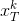
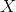
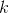
其中,假设项是固定的,我们要更新的是第
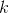
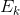
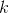
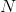
也许有人会尝试利用SVD得到可选的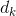
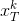
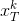
有一个简单直观的方法可以解决上面问题。
定义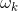
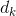
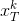
定义大小为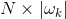
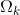
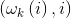
定义向量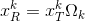
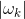
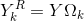
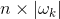
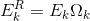
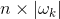
中非零位置相对应的那些列。
现在回到问题(2),由于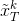
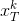
现在可以直接用SVD解决问题(3),得到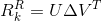
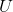
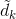
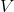
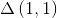
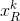
此解决方案必须满足两个条件:i)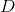
字典列的更新与稀疏表示系数更新结合在一起加快了算法的收敛。
下图截自原论文,其中详细描述了K-SVD算法。
总结
K-SVD一般用在字典学习中,是K-means的扩展形式。
为何叫K-SVD,是因为在字典的K个代表中,求解的时候才用的是SVD分解
下面讲讲K-SVD的核心
我 们在sparse representation中知道,||Y-Dx||^2,||x||的0范都足够最小的时候,就是表示我们的字典D最好的时候,其 含义就是我要寻找字典D,并且x中的每个向量要足够稀疏,使得Y能够被字典D在一定的误差内给表示出来。这个就是核心。(当然,在训练D的时候,有人会 想,我就用训练集Y来代替字典不就可以了吗?是可以,但是这样在你以后用字典重构其他数据的时候,计算时间会很高,所以为何要减少D中的数量,以典型的代 表来代表这个字典)。
我们假设dj为D中的第j个向量,那么我们的思想是一次我就优化一个字典向量,优化完了就优化第二个,然后再迭代上面的步骤,一直到误差小于某个范围的时候就可以了。
那么我们的式子可以描述为 minimize||Y-SUM(j=1 to k ( dj * xjt ))||,其中xjt表示X中的第j行
设Q=Y-(D-di*xit),那么上面可以描述为||Q- di*xit||,那么到这里就基本上差不多了。
怎么更新di和xi呢
可以对Q进行SVD分解,分解为UEV的形式,然后将U的第一列(类似于最大主元)给di,将E的第一个奇异值乘以V的第一行元素赋值给xi,然后按照上述方法更新下一个d和x
但 是这里我们要注意,我们必须要是xi满足稀疏,那么我们这里要做一些处理,以xi的非零元素的位置构建一个矩阵,矩阵为N*M(M是xi的非零元素的个 数,N为字典中每个向量的维数)的O矩阵,然后将一Y,Pi,xi更新为Y*O, Pi*O,xit*O,得到新的||Q-di*xit||,这个时候在 才用上面的SVD即可,
这里谈下为什么,上面乘以O的操作其实就是把字典中没有做贡献的向量给移除掉,从而将字典空间和xi都缩减了,这样就不会造成直接分解之前的Q的时候种V的行向量不是稀疏的性质了。
至 于为何要选用SVD,当你把SVD的最大的特征值对应的U,V向量取出来的时候,相当于一个列向量乘以一个行向量,在乘上大小 ,是不是很类似与LSA, 而且就满足了dj和xjt相乘的形式。还有一个感性的认识就是,既然要减小||Q- di*xit||,那么只需要当di,xit等于最大的左特正向量和 右特征向量的时候,就代表了最大的接近去Q的形式了,是不是很类似最大主元PCA的方法???
就这样吧,个人理解,有纰漏还希望大家见谅,多多指正
转载地址:http://blog.nrdang.com/?p=35








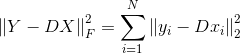
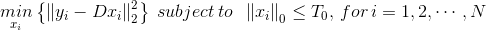
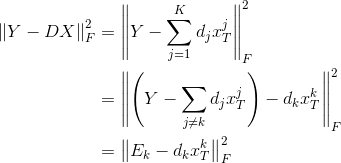
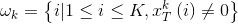
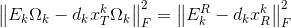















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








