URAL 1204

最新推荐文章于 2018-11-28 23:16:29 发布

置顶 Jsun-moon

最新推荐文章于 2018-11-28 23:16:29 发布

阅读量957

点赞数

分类专栏： ural 数学文章标签： ural 1204 Idempotents

本文链接：https://blog.csdn.net/jsun_moon/article/details/9874847

版权

ural 数学专栏收录该内容

23 篇文章 0 订阅

订阅专栏

题目大意：求解k个方程：x^2=x(mod ni)(i=1,2,...,k)，其中ni=p*q，p和q均为素数。

Time Limit:1000MS Memory Limit:65536KB 64bit IO Format:%I64d & %I64u

数据规模：1<=k<=1000，ni<=10^9(i=1,2,...,k)。

理论基础：

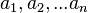中国剩余定理：若有一些两两互质的整数 $m_1, m_2, \ldots, m_n$ ，则对任意的整数： $a_1, a_2,...a_n$ ，以下联立同余方程组对模 $m_1 m_2 \cdots m_n$ 有公解：x=ai(mod mi)(i=1,2,3,...)。

扩展欧几里得算法：若有方程：a*x+b*y=gcd(a,b);

那么：a*x+b*y=gcd(b,mod(a,b))=b*x0+mod(a,b)*y0

=b*x0+(a-a/b*b)*y0

=a*y0+b*(x0-a/b*y0)

所以：x=y0,y=(x0-a/b*y0)。这样递归下去，还和以前的分析方法一样要想找到终止状态，那么我们要看什么在变，什么不变，很明显b一直在变小，由欧几里得算法可知b==0是即可终止。此时gcd(a,b)=a(终止时的a),x=1,y=0。再返带回去，我们就有x与y的解了。

题目分析：不对啊。人家让求的是一元二次同余方程，又不是一次同余方程组，你讲那个理论有毛用？别急，你再接着看看。x^2=x(mod n)<==>x*（x-1)=0(mod p*q)，因为：p与q互质，x与x-1互质,|那么必有：x=0（mod p），x=1(mod q)或者x=0（mod p），x=1(mod q)。这不就是一次同余方程组嘛？然后，我们就可以得出:x=a*p，x=-b*q+1，那么：a*p+b*q=1（另一种情况是一样的方程），这么还不够明显？那这样写？x*p+y*q=gcd(p,q)=1。这下求出a，那x=a*p(mod n),x=b*q(mod n)，不就是两种情况下的解？当然我们还可以观察出一组通解：x=0,x=1，不信你就带进去试试。是不是感觉很有趣？精彩还在后面，数论是一个让人着迷的领域。

代码如下：

#include<iostream>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
typedef double db;
#define DBG 1
#define maa (1<<31)
#define mii ((1<<31)-1)
#define sl(c) ((int)(c).size())    //取字符串长度；
#define forl(i, a, b) for(int i = (a); i <  (b); ++i)    //不带边界值循环，正序
#define forle(i, a, b) for(int i = (a); i <= (b); ++i)   //带边界值循环，正序
#define forh(i, a, b) for(int i = (a); i >  (b); --i)     //不带边界值，逆序
#define forhe(i, a, b) for(int i = (a); i >= (b); --i)        //带边界值，逆序
#define forlc(i, a, b) for(int i##_b = (b), i = (a); i <  i##_b; ++i)  //带别名的循环，用于不可改变值
#define forlec(i, a, b) for(int i##_b = (b), i = (a); i <= i##_b; ++i)
#define forgc(i, a, b) for(int i##_b = (b), i = (a); i >  i##_b; --i)
#define forgec(i, a, b) for(int i##_b = (b), i = (a); i >= i##_b; --i)
#define forall(i, v   )  forl(i, 0, sz(v))   //循环所有
#define forallc(i, v   ) forlc(i, 0, sz(v))
#define forlla(i, v   ) forhe(i, sz(v)-1, 0)
#define forls(i, n, a, b) for(int i = a; i != b; i = n[i])   //搜表用
#define rep(n)  for(int               repp = 0; repp <    (n); ++repp)
#define repc(n) for(int repp_b = (n), repp = 0; repp < repp_b; ++repp)
#define rst(a, v) memset(a, v, sizeof a)   //把字符v填充到a  reset 重置
#define cpy(a, b) memcpy(a, b, sizeof a)   //copy b 的sizeof（a）个字符到a
#define rstn(a, v, n) memset(a, v, (n)*sizeof((a)[0]))  //把字符v填充到a[n]之前的字节
#define cpyn(a, b, n) memcpy(a, b, (n)*sizeof((a)[0]))    //copy b 的 n 个字符到a
#define ast(b) if(DBG && !(b)) { printf("%d!!|\n", __LINE__); while(1) getchar(); }  //调试
#define dout DBG && cout << __LINE__ << ">>| "
#define pr(x) #x"=" << (x) << " | "
#define mk(x) DBG && cout << __LINE__ << "**| "#x << endl
#define pra(arr, a, b)  if(DBG) {\
    dout<<#arr"[] |" <<endl; \
    forlec(i, a, b) cout<<"["<<i<<"]="<<arr[i]<<" |"<<((i-(a)+1)%8?" ":"\n"); \
    if((b-a+1)%8) puts("");\
}                                                             //数列查看
#define rd(type, x) type x; cin >> x   //读数
inline int     rdi() { int d; scanf("%d", &d); return d; }
inline char    rdc() { scanf(" "); return getchar(); }
inline string  rds() { rd(string, s); return s; }
inline db rddb() { db d; scanf("%lf", &d); return d; }
template<class T> inline bool updateMin(T& a, T b) { return a>b? a=b, true: false; }
template<class T> inline bool updateMax(T& a, T b) { return a<b? a=b, true: false; }

long long n;
int T;
struct triple
{
    int x,y,d;
};
inline int mod(int a,int b)   //求a(mod b)；
{
    if(a >= 0)
        return a % b;
    else
        return a % b + b;
}
inline void breakup(int n,int &p,int &q)  //分解n.
{
    for(int i=2;i*i<=n;i++)
    {
        if(n%i==0)
        {
            p=i;
            q=n/i;
            break;
        }
    }
}
triple Extented_Euclid(int a,int b)
//Euclid扩展欧几里得算法。求解：x≡0(p)&&x≡1(q)<==>a*p+b*q=1;求出a与b；
{
    triple result;
    if(b==0)
    {
        result.x=1;
        result.y=0;
        result.d=a;
    }
    else
    {
        triple temp=Extented_Euclid(b,mod(a,b));   //递归调用
        result.d=temp.d;
        result.x=temp.y;
        result.y=temp.x-(a/b)*temp.y;
    }
    return result;
}

int main()
/*
转化为p*q|x(x-1)。
x%p=0,x%q=1以及x%q=0,x%p=1。
第一种情况，就是中国剩余定理的一种最简单例子。那么有唯一解。具体见代码。
另一种情况同理可得。
*/
{
    triple t;
    T=rdi();
    while(T--)
    {
        int p,q,x1,x2;
        n=rdi();
        breakup(n,p,q);
        t=Extented_Euclid(p,q);
        x1=mod((p*t.x),n);
        x2=mod((q*t.y),n);
        if(x1>x2)
        {
            int temp=x1;
            x1=x2;
            x2=temp;
        }
        printf("0 1 %d %d\n",x1,x2);
    }
	return 0;
}

其中，使用结构体带回返回值较为方便，推荐大家以后使用。

http://zh.wikipedia.org/wiki/%E4%B8%AD%E5%9B%BD%E5%89%A9%E4%BD%99%E5%AE%9A%E7%90%86

by:Jsun_moon http://blog.csdn.net/Jsun_moon