Aizu 2223

Time Limit:8000MS     Memory Limit:65536KB     64bit IO Format:%lld & %llu

Submit  Status  Practice  Aizu 2223

Description

There is a frog living in a big pond. He loves jumping between lotus leaves floating on the pond. Interestingly, these leaves have strange habits. First, a leaf will sink into the water after the frog jumps from it. Second, they are aligned regularly as if they are placed on the grid points as in the example below.

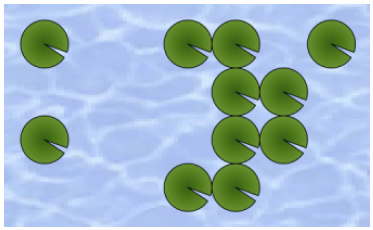
Figure 1: Example of floating leaves

Recently, He came up with a puzzle game using these habits. At the beginning of the game, he is on some leaf and faces to the upper, lower, left or right side. He can jump forward or to the left or right relative to his facing direction, but not backward or diagonally. For example, suppose he is facing to the left side, then he can jump to the left, upper and lower sides but not to the right side. In each jump, he will land on the nearest leaf on his jumping direction and face to that direction regardless of his previous state. The leaf he was on will vanish into the water after the jump. The goal of this puzzle is to jump from leaf to leaf until there is only one leaf remaining.

See the example shown in the figure below.

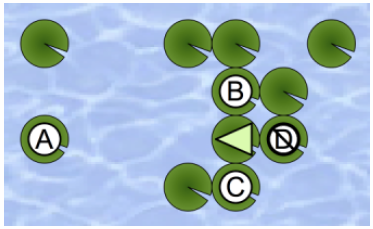
In this situation, he has three choices, namely, the leaves A, B and C. Note that he cannot jump to the leaf D since he cannot jump backward. Suppose that he choose the leaf B. After jumping there, the situation will change as shown in the following figure.

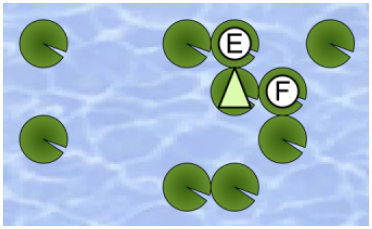
He can jump to either leaf E or F next.

After some struggles, he found this puzzle difficult, since there are a lot of leaves on the pond. Can you help him to find out a solution?

Input

H W
c_1,1 ... c_1,W
.
.
.
c_H,1 ... c_H,W

The first line of the input contains two positive integers H and W (1 ≤ H,W ≤ 10). The following H lines, which contain W characters each, describe the initial configuration of the leaves and the frog using following characters:

• '.’ : water
• ‘o’ : a leaf
• ‘U’ : a frog facing upward (i.e. to the upper side) on a leaf
• ‘D’ : a frog facing downward (i.e. to the lower side) on a leaf
• ‘L’ : a frog facing leftward (i.e. to the left side) on a leaf
• ‘R’ : a frog facing rightward (i.e. to the right side) on a leaf

You can assume that there is only one frog in each input. You can also assume that the total number of leaves (including the leaf the frog is initially on) is at most 30.

Output

Output a line consists of the characters ‘U’ (up), ‘D’ (down), ‘L’ (left) and ‘R’ (right) that describes a series of movements. The output should not contain any other characters, such as spaces. You can assume that there exists only one solution for each input.

Sample Input 1

2 3
Uo.
.oo

Output for the Sample Input 1

RDR

Sample Input 2

10 10
.o....o...
o.oo......
..oo..oo..
..o.......
..oo..oo..
..o...o.o.
o..U.o....
oo......oo
oo........
oo..oo....

Output for the Sample Input 2

URRULULDDLUURDLLLURRDLDDDRRDR

Sample Input 3

10 1
D
.
.
.
.
.
.
.
.
o

Output for the Sample Input 3

D

#include <iostream>
#include <string>
#include <string.h>
#include <fstream>

using namespace std;

#define MAXN 11

int n, m, s, e, d, total;
int c[MAXN][MAXN];
int dir[4][2] = {0, -1, -1, 0, 0, 1, 1, 0};
int ans[MAXN * MAXN];
bool ok;

int change(char ch)
{
    switch(ch)
    {
        case 'L': return 0;
        case 'U': return 1;
        case 'R': return 2;
        case 'D': return 3;
    }
}

char changetwo(int x)
{
    switch(x)
    {
        case 0: return 'L';
        case 1: return 'U';
        case 2: return 'R';
        case 3: return 'D';
    }
}

void dfs(int x, int y, int len, int di)
{
    if (len == total)
    {
        ok = true;
        return ;
    }

    if (ok)
    {
        return ;
    }

    for (int i = 3; i < 6; i++)
    {
        for (int k = 1; k <= 10; k++)
        {
            int xt = x + dir[(i + di) % 4][0] * k, yt = y + dir[(i + di) % 4][1] * k;

            if (xt >= 0 && xt < n && yt >= 0 && yt < m && !ok) //注意
            {
                if (c[xt][yt] == 1)
                {
                    ans[len] = (i + di) % 4;
                    len++;
                    c[xt][yt] = 0;
                    dfs(xt, yt, len, (i + di) % 4);

                    len--;
                    c[xt][yt] = 1;
                    break;
                }
            }
        }
    }
}

void solve()
{
    dfs(s, e, 0, d);

    for (int i = 0; i < total; i++)
    {
        cout << changetwo(ans[i]);
    }
    cout << endl;
}

void input()
{
    char ch;

    while (cin >> n >> m)
    {
        total = 0;
        ok = false;
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
                cin >> ch;
                if (ch == '.')
                {
                    c[i][j] = 0;
                }
                else if (ch == 'o')
                {
                    total++;
                    c[i][j] = 1;
                }
                else
                {
                    d = change(ch);
                    s = i, e = j;
                    c[i][j] = 0;
                }
            }
        }

        solve();
    }
}

int main()
{
    std::ios::sync_with_stdio(false);
    input();
    return 0;
}