用python实现解常微分方程组的简单示例以及用odeint解常微分方程的范例

背景：

包括两个部分，一个是演示怎么自己写代码解常微分方程，另一部分就是示范python怎么调用解常微分方程的函数。

下面的方程组给出洛仑兹引子在三个方向上的速度，求解运动轨迹

软件：

python3.5.2

部分1：(div)

代码：

# -*- coding: utf8 -*-
import numpy as np
"""
移动方程：
t时刻的位置P(x,y,z)
steps：dt的大小
sets：相关参数
"""
def move(P,steps,sets):
    x,y,z = P
    sgima,rho,beta = sets
    #各方向的速度近似
    dx = sgima*(y-x)
    dy = x*(rho-z)-y
    dz = x*y - beta*z
    return [x+dx*steps,y+dy*steps,z+dz*steps]

#设置sets参数
sets = [10.,28.,3.]
t = np.arange(0,30,0.01)

#位置1：
P0 = [0.,1.,0.]

P = P0
d = []
for v in t:
    P = move(P,0.01,sets)
    d.append(P)
dnp = np.array(d)

#位置2：
P02 = [0.,1.01,0.]

P = P02
d = []
for v in t:
    P = move(P,0.01,sets)
    d.append(P)
dnp2 = np.array(d)
"""
画图
"""
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

fig = plt.figure()
ax = Axes3D(fig)
ax.plot(dnp[:,0],dnp[:,1],dnp[:,2])
ax.plot(dnp2[:,0],dnp2[:,1],dnp2[:,2])
plt.show()

结果：

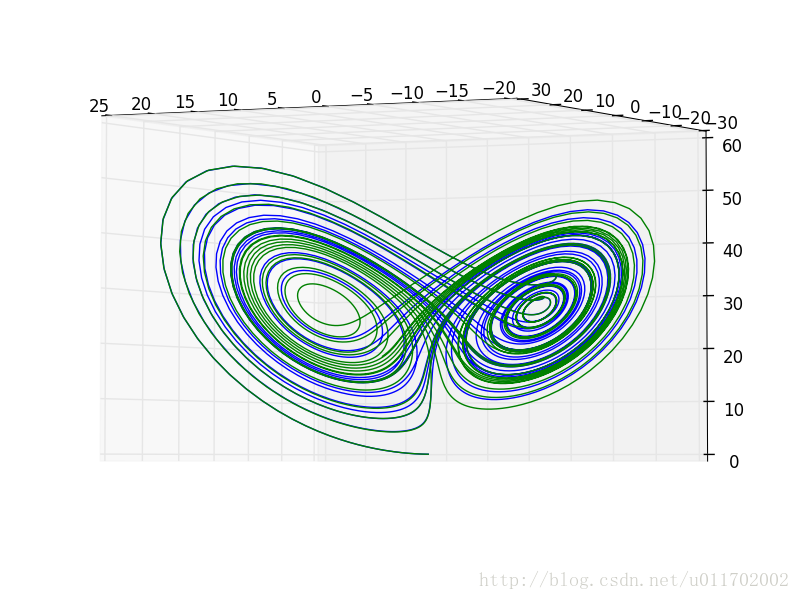
部分2：

代码：

# -*- coding: utf-8 -*-
import numpy as np
from scipy.integrate import odeint
"""
定义常微分方程，给出各方向导数,即速度
"""
def dmove(Point,t,sets):
    """
    p：位置矢量
    sets：其他参数
    """
    p,r,b = sets
    x,y,z = Point
    return np.array([p*(y-x),x*(r-z),x*y-b*z])

t = np.arange(0,30,0.01)
#调用odeint对dmove进行求解，用两个不同的初始值
P1 = odeint(dmove,(0.,1.,0.),t,args = ([10.,28.,3.],))  #(0.,1.,0.)是point的初值
#([10.,28.,3.],)以元祖的形式给出 point,t之后的参数
P2 = odeint(dmove,(0.,1.01,0.),t,args = ([10.,28.,3.],))

"""
画3维空间的曲线
"""
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

fig = plt.figure()
ax = Axes3D(fig)
ax.plot(P1[:,0],P1[:,1],P1[:,2])
ax.plot(P2[:,0],P2[:,1],P2[:,2])
plt.show()

结果：