AR模型:
具有如下结构的模型称为p阶自回归模型,简记为AR(p):
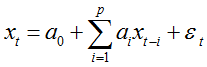
AR(p)模型有三个限制条件:
-
。保证模型的最高阶数为p。
-
随机干扰项序列
为零均值白噪声序列。
-
当期的随机干扰项与过去的序列值无关,即:
中心化AR(p)模型:
当a0=0时,自回归模型称为中心化AR(p)模型。非中心化AR(p)模型可以通过下面的变化转换为中心化AR(p)序列。
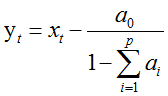
P阶自回归系数多项式:
引进延迟算子B:
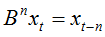
则中心化AR(p)模型可以简记为:
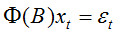
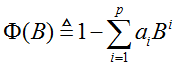
AR模型平稳性判别:
特征根判别法:
将AR(p)模型看作一个非齐次线性方程:
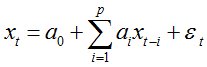
-
齐次线性差分方程的通解:
由线性差分方程的相关理论可以知道齐次线性方程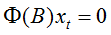
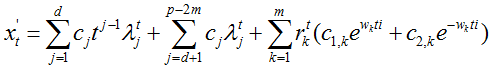
其中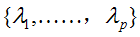
-
非齐次线性差分方程的的特解:
可以证明AR(P)模型的自回归系数多项式方程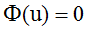
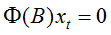
-
自回归系数多项式方程
-
的特征方程:
因此,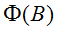
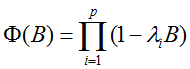
由此可以得到一个特解:
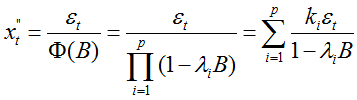
-
非齐次线性差分方程
的通解:
要使得AR(p)模型平稳,即要求对任意的实数{ci},都有
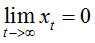
即可得到AR(p)平稳的充要条件:
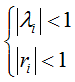
上面的条件实际上就是要求AR(p)模型的p个特征根都在单位圆内。由特征根与自回归系数多项式的根成倒数的性质,也即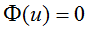
平稳域判别法:
-
AR(1)模型的平稳域:
-
AR(2)模型的平稳域:
平稳AR模型的统计特征:
均值:
在AR(p)模型等式两边取均值:

由平稳序列均值为常数,以及{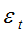
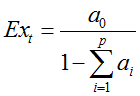
中心化的AR(p)模型均值为0.
方差:
求AR(p)模型的方差需要借助Green函数,附录中给出了详细推导。
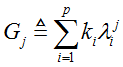
Gj函数的递推公式如下:
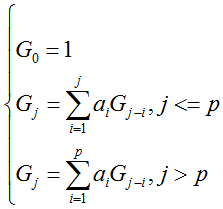
则:
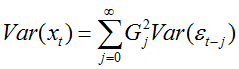
由于{
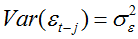
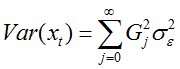
平稳AR(1)模型的方差:
可以很容易得出此时格林函数的递推式:
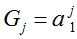
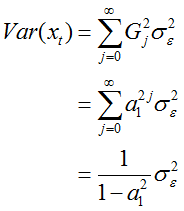
自协方差:
对中心化AR(p)模型两边同乘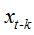

由AR(p)模型的限制条件3有
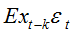
故可以得到自协方差函数的递推公式:

平稳AR(1)模型的自协方差函数
AR(1)的自协方差函数递推关系式为:
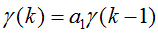
又
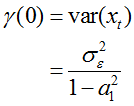
所以:

自相关系数:
由于自相关系数和自协方差有如下的关系:
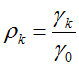
可以得到自相关系数的递推式:
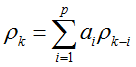
平稳AR(1)模型的自相关系数:
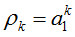
附录:
平稳AR(p)模型的方差推导:

令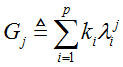
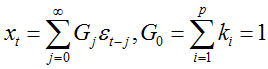
记
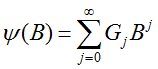
则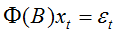
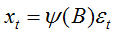
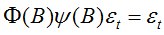
展开整理:

又:
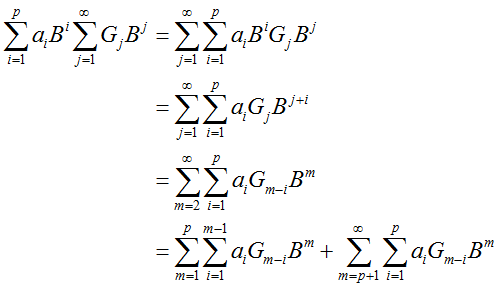
且:
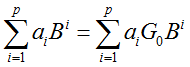
整理后两项
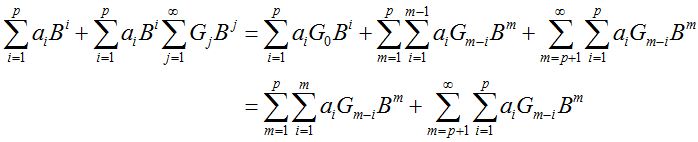
所以:
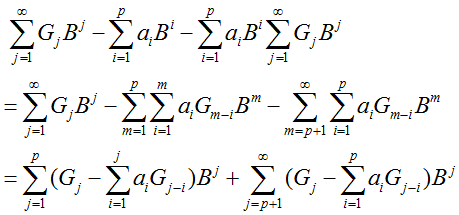
有:
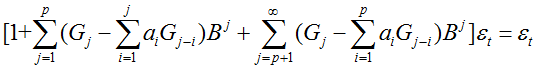
由待定系数法可以得到Green函数的递推式:
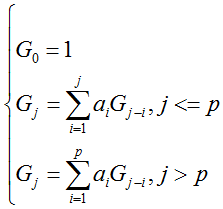








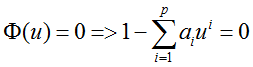
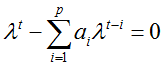
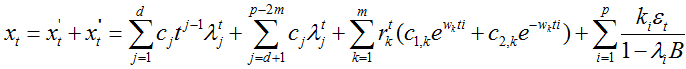
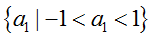
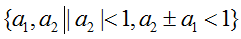
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








