hdu 1025 （LIS（n*log(n)时间复杂度））

Constructing Roads In JGShining's Kingdom

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 14099    Accepted Submission(s): 4008

Problem Description

 

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.

Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.  

With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.

Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.  

The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.  

But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.

For example, the roads in Figure I are forbidden.



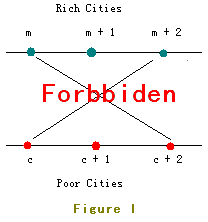
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

 

 

Input

 

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.

 

 

Output

 

For each test case, output the result in the form of sample.  
You should tell JGShining what's the maximal number of road(s) can be built.  

 

 

Sample Input

 

  
  

   
   2
1 2
2 1
3
1 2
2 3
3 1
  
  

 

 

Sample Output

 

  
  

   
   Case 1:
My king, at most 1 road can be built.

Case 2:
My king, at most 2 roads can be built.
  
  

 

最长上升子序列的O(n＊logn)算法分析如下:

先回顾经典的O(n＾2)的动态规划算法，设a[t]表示序列中的第t个数，dp[t]表示从1到t这一段中以t结尾的最长上升子序列的长度，初始时设dp [t] = 0(t = 1, 2, ..., len(a))。则有动态规划方程：dp[t] = max{1, dp[j] + 1} (j = 1, 2, ..., t - 1, 且a[j] < a[t])。 

现在，我们仔细考虑计算dp[t]时的情况。假设有两个元素a[x]和a[y]，满足 

(1)x < y < t

(2)a[x] < a[y] < a[t]

(3)dp[x] = dp[y]

此时，选择dp[x]和选择dp[y]都可以得到同样的dp[t]值，那么，在最长上升子序列的这个位置中，应该选择a[x]还是应该选择a[y]呢？ 

很明显，选择a[x]比选择a[y]要好。因为由于条件(2)，在a[x+1] ... a[t-1]这一段中，如果存在a[z]，a[x] < a[z] < a[y]，则与选择a[y]相比，将会得到更长的上升子序列。 

再根据条件(3)，我们会得到一个启示：根据dp[]的值进行分类。对于dp[]的每一个取值k，我们只需要保留满足dp[t] = k的所有a[t]中的最小值。设D[k]记录这个值，即D[k] = min{a[t]} (dp[t] = k)。 

注意到D[]的两个特点： 

(1)　D[k]的值是在整个计算过程中是单调不上升的。 

(2)　D[]的值是有序的，即D[1] < D[2] < D[3] < ... < D[n]。 

利用D[]，我们可以得到另外一种计算最长上升子序列长度的方法。设当前已经求出的最长上升子序列长度为len。先判断a[t]与D[len]。若a [t] > D[len]，则将a[t]接在D[len]后将得到一个更长的上升子序列，len = len + 1， D[len] = a [t]；否则，在D[1]..D[len]中，找到最大的j，满足D[j] < a[t]。令k = j + 1，则有a [t] <= D[k]，将a[t]接在D[j]后将得到一个更长的上升子序列，更新D[k] = a[t]。最后，len即为所要求的最长上 升子序列的长度。 

在上述算法中，若使用朴素的顺序查找在D[1]..D[len]查找，由于共有O(n)个元素需要计算，每次计算时的复杂度是O(n)，则整个算法的时间复杂度为O(n^2)，与原来的算法相比没有任何进步。但是由于D[]的特点(2)，我们在D[]中查找时，可以使用二分查找高效地完成，则整个算法的时间复杂度下降为O(nlogn)，有了非常显著的提高。需要注意的是，D[]在算法结束后记录的并不是一个符合题意的最长上升子序列！

 

#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
#define ll __int64
#define mem(a,t) memset(a,t,sizeof(a))
#define N 500005
const int inf=0x7fffffff;
int a[N];
int c[N];
int findd(int x,int l,int r) //找到最小的大于等于它的数
{
    int mid;
    while(l<=r)
    {
        mid=(l+r)>>1;
        if(c[mid]==x)
            return mid;
        if(c[mid]<x)
            l=mid+1;
        else
            r=mid-1;
    }
    return l;
}

int main()
{
    //freopen("in.txt","r",stdin);
    int i,cnt=1,r,x,t,n,len;
    while(scanf("%d",&n)!=-1)
    {
        for(i=0;i<n;i++)
        {
            scanf("%d%d",&x,&r);
            a[x]=r;
        }
        c[0]=a[1];
        len=1;
        for(i=2;i<=n;i++)
        {
            if(a[i]>c[len-1])
                c[len++]=a[i];
            else
            {
                t=findd(a[i],0,len);
                c[t]=a[i];
            }
        }
        printf("Case %d:\n",cnt++);
        if(len==1)
            printf("My king, at most %d road can be built.\n\n",len);
        else
            printf("My king, at most %d roads can be built.\n\n",len);
    }
    return 0;
}