【金九银十】笔试通关 + 小学生都能学会的希尔排序-CSDN博客

本文链接：https://blog.csdn.net/u012263509/article/details/142750594

请在此添加图片描述

希尔排序（Shell Sort）是一种改进的插入排序算法。其基本思想是将待排序的数组分成若干个子序列，对每个子序列进行插入排序，然后逐步减少子序列的间隔（称为“增量”），最终当增量为1时，对整个序列进行插入排序。通过这种方式，希尔排序在排序过程中能够减少元素的移动次数，提高了插入排序的效率。

起源

希尔排序由计算机科学家 Donald Shell 于 1959 年提出。Shell 的目标是改进插入排序，使其在处理大规模数据时效率更高。希尔排序的核心思想在于通过逐步减少元素间的间隔，使得数据在插入排序时更加接近有序，从而提高排序效率。

算法原理

选择增量序列：首先选择一个增量序列，例如，希尔增量序列（通常是逐步减小的整数序列）。
分组排序：根据当前增量，将待排序序列分成若干个子序列，每个子序列包含的元素间隔为当前增量。对每个子序列进行插入排序。
减少增量：逐步减少增量，重复步骤2，直到增量为1。
最后排序：当增量为1时，进行最后的插入排序，使整个序列有序。

实例分析

考虑一个待排序的数组：[9, 8, 7, 6, 5, 4, 3, 2, 1]

假设增量序列为 [5, 3, 1]（这只是一个例子，实际的增量序列可以有所不同）：

增量 5：

- 子序列1: [9, 4]
- 子序列2: [8, 3]
- 子序列3: [7, 2]
- 子序列4: [6, 1]

对每个子序列进行插入排序。

增量 3：

- 子序列1: [9, 8, 7]
- 子序列2: [6, 5, 4]
- 子序列3: [3, 2, 1]

对每个子序列进行插入排序。

增量 1：

- 对整个序列进行插入排序。

动态实现

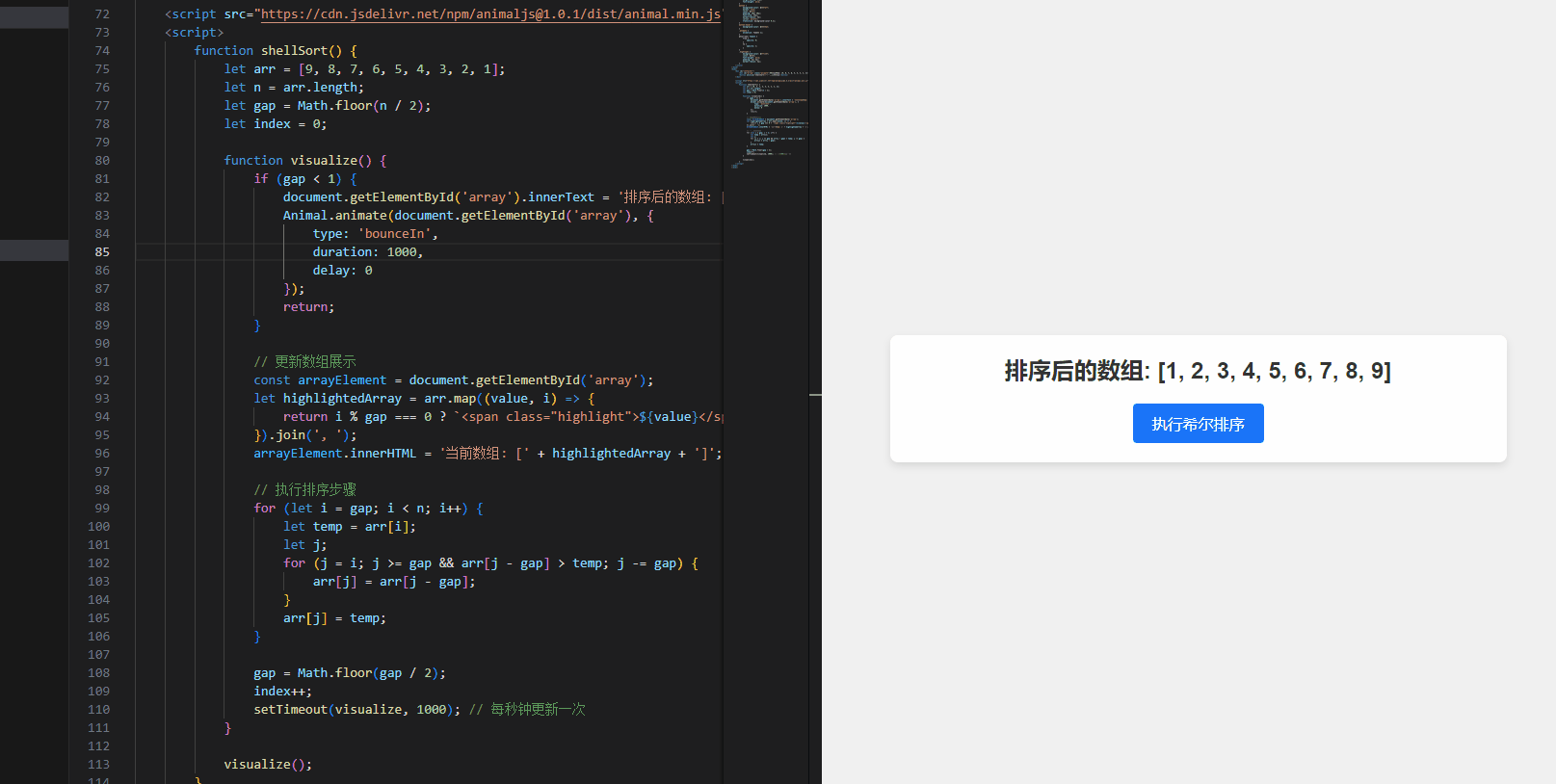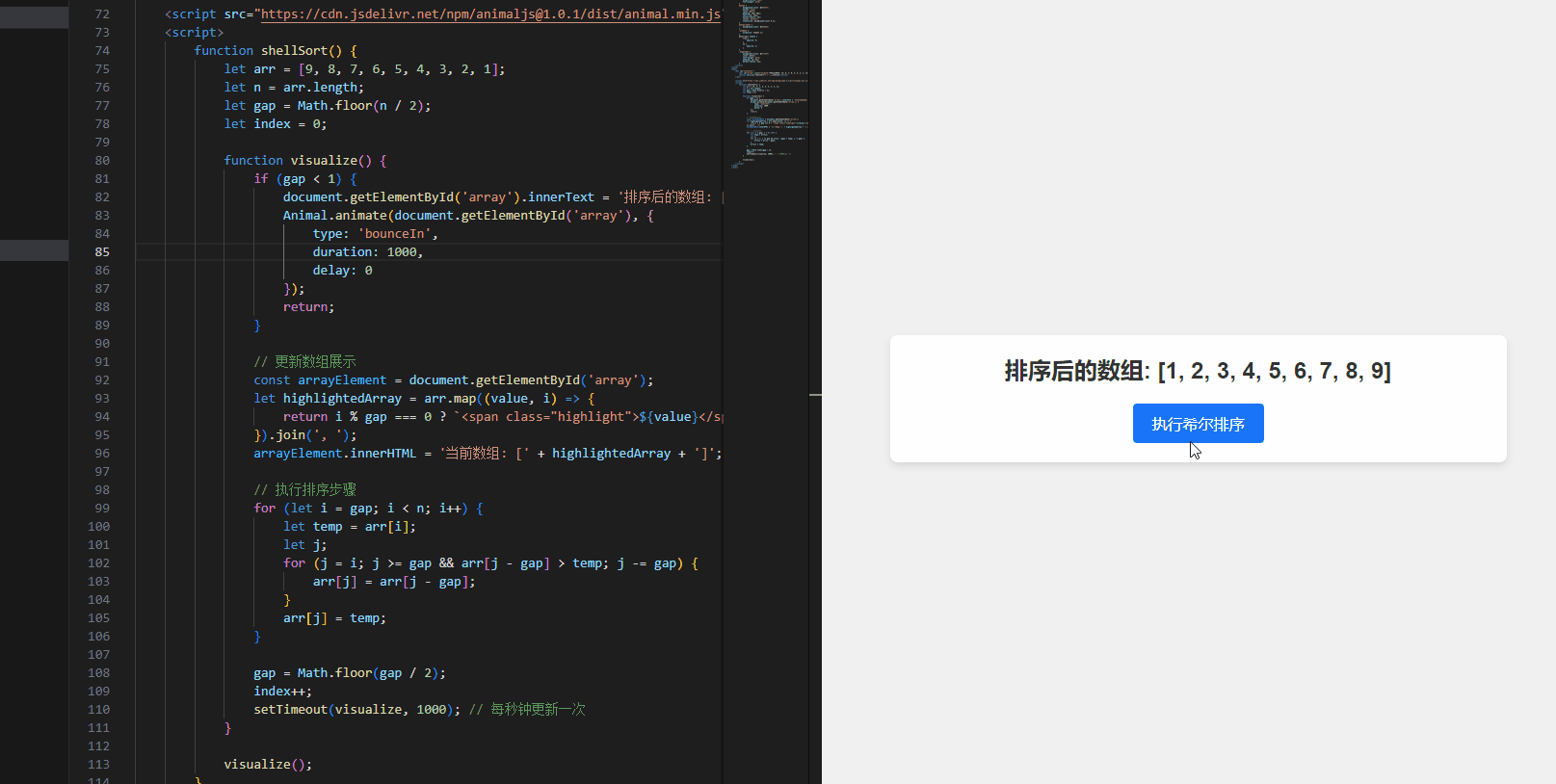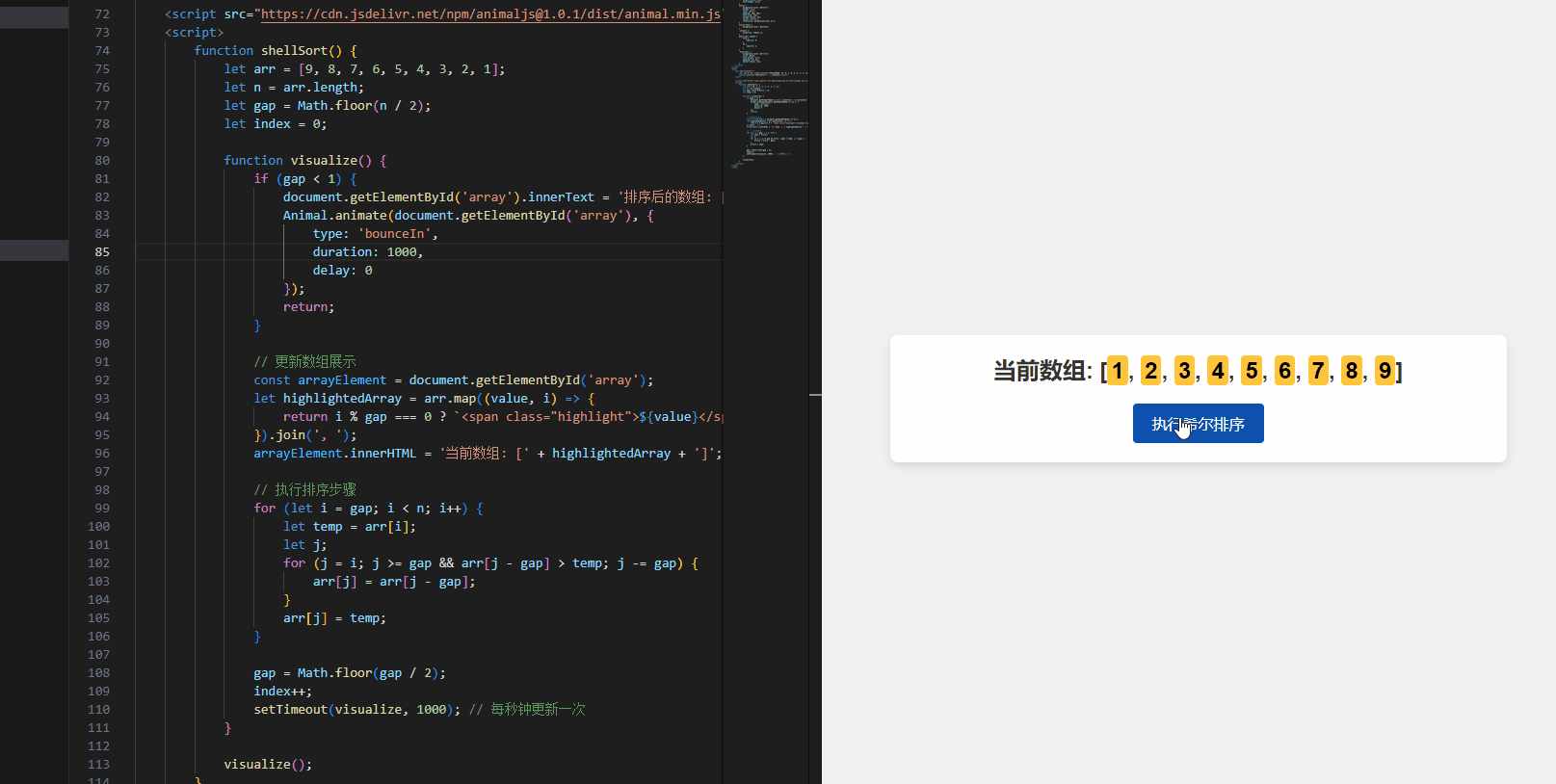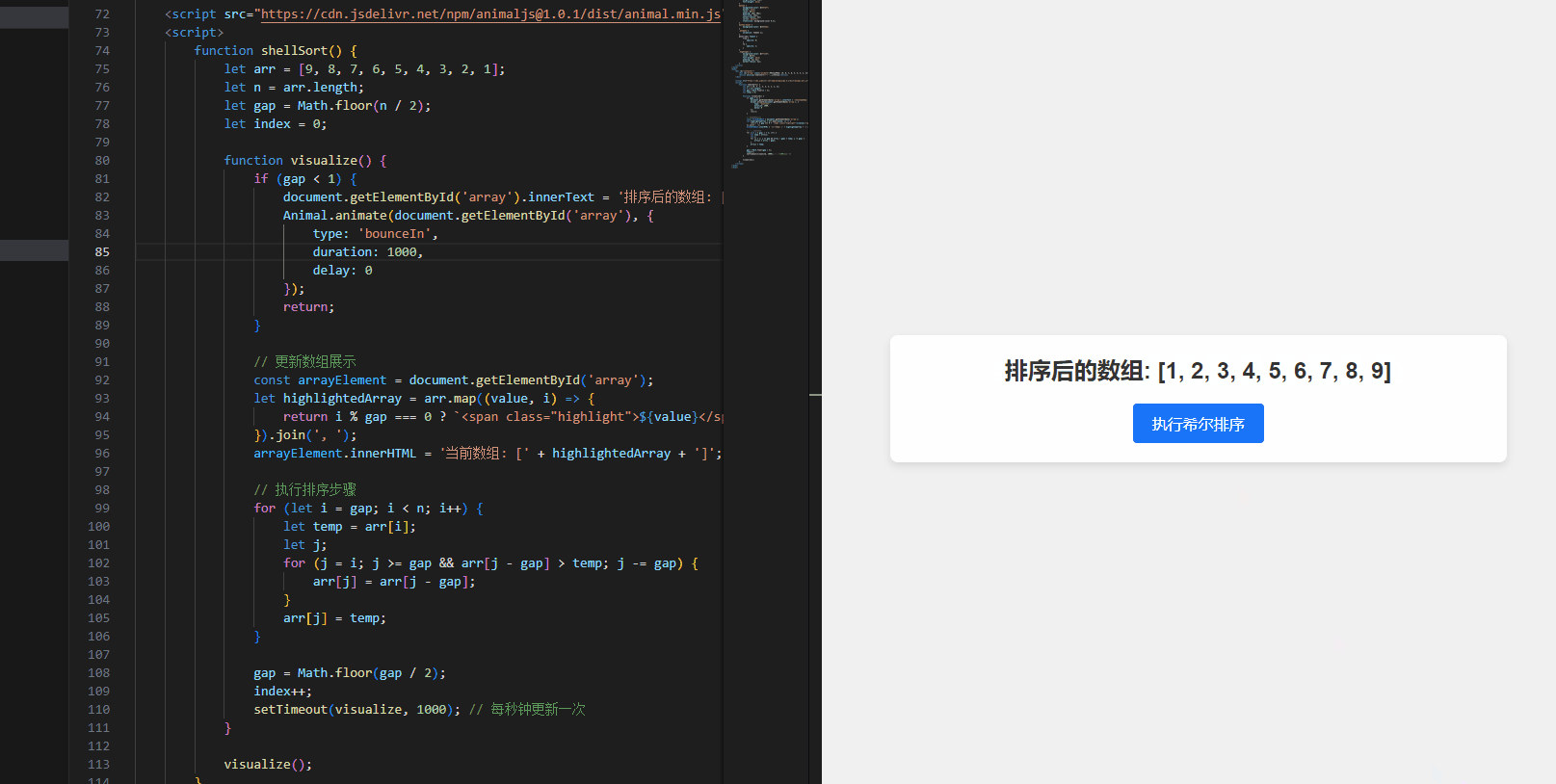
下面是一个简单的HTML和JavaScript实现希尔排序的示例：

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>希尔排序示例</title>
    <link rel="stylesheet" href="https://cdnjs.cloudflare.com/ajax/libs/animate.css/4.1.1/animate.min.css">
    <style>
        body {
            font-family: Arial, sans-serif;
            background: #f0f0f0;
            color: #333;
            display: flex;
            justify-content: center;
            align-items: center;
            height: 100vh;
            margin: 0;
        }
        #container {
            text-align: center;
            background: #fff;
            border-radius: 8px;
            box-shadow: 0 4px 8px rgba(0, 0, 0, 0.1);
            padding: 20px;
            width: 80%;
            max-width: 600px;
        }
        #array {
            font-size: 24px;
            margin-bottom: 20px;
            font-weight: bold;
        }
        button {
            background-color: #007bff;
            border: none;
            color: #fff;
            padding: 10px 20px;
            font-size: 16px;
            border-radius: 4px;
            cursor: pointer;
            transition: background-color 0.3s;
        }
        button:hover {
            background-color: #0056b3;
        }
        .animate {
            animation: fadeIn 1s;
        }
        @keyframes fadeIn {
            from {
                opacity: 0;
            }
            to {
                opacity: 1;
            }
        }
        .highlight {
            background-color: #ffc107;
            color: #000;
            font-weight: bold;
            padding: 2px 4px;
            border-radius: 4px;
        }
    </style>
</head>
<body>
    <div id="container">
        <div id="array" class="animate">待排序数组: [9, 8, 7, 6, 5, 4, 3, 2, 1]</div>
        <button onclick="shellSort()">执行希尔排序</button>
    </div>

    <script src="https://cdn.jsdelivr.net/npm/animaljs@1.0.1/dist/animal.min.js"></script>
    <script>
        function shellSort() {
            let arr = [9, 8, 7, 6, 5, 4, 3, 2, 1];
            let n = arr.length;
            let gap = Math.floor(n / 2);
            let index = 0;

            function visualize() {
                if (gap < 1) {
                    document.getElementById('array').innerText = '排序后的数组: [' + arr.join(', ') + ']';
                    Animal.animate(document.getElementById('array'), {
                        type: 'bounceIn',
                        duration: 1000,
                        delay: 0
                    });
                    return;
                }

                // 更新数组展示
                const arrayElement = document.getElementById('array');
                let highlightedArray = arr.map((value, i) => {
                    return i % gap === 0 ? `<span class="highlight">${value}</span>` : value;
                }).join(', ');
                arrayElement.innerHTML = '当前数组: [' + highlightedArray + ']';

                // 执行排序步骤
                for (let i = gap; i < n; i++) {
                    let temp = arr[i];
                    let j;
                    for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                        arr[j] = arr[j - gap];
                    }
                    arr[j] = temp;
                }

                gap = Math.floor(gap / 2);
                index++;
                setTimeout(visualize, 1000); // 每秒钟更新一次
            }

            visualize();
        }
    </script>
</body>
</html>

请在此添加图片描述

代码解释

以下是希尔排序算法的代码及其详细解释：

function shellSort() {
    let arr = [9, 8, 7, 6, 5, 4, 3, 2, 1];
    let n = arr.length;
    let gap = Math.floor(n / 2); // 选择初始增量

    // 逐步减少增量，直到增量为1
    while (gap > 0) {
        // 对每个增量下的子序列进行插入排序
        for (let i = gap; i < n; i++) {
            let temp = arr[i]; // 需要插入的元素
            let j;
            // 移动元素，找到插入位置
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                arr[j] = arr[j - gap]; // 移动元素
            }
            arr[j] = temp; // 插入元素
        }
        gap = Math.floor(gap / 2); // 减少增量
    }

    // 输出排序后的数组
    document.getElementById('array').innerText = '排序后的数组: [' + arr.join(', ') + ']';
}

详细解释

初始化增量：初始增量是数组长度的一半。增量的选择对于排序性能有很大影响，较大的增量可以让数据更快接近有序。

let gap = Math.floor(n / 2);

外层循环：外层循环控制增量的逐步减小。每次迭代中，我们会对当前增量下的子序列进行排序。

while (gap > 0) {

内层循环：内层循环遍历每个子序列中的元素，执行插入排序。temp 保存当前要插入的元素。

for (let i = gap; i < n; i++)

移动元素：这个循环将当前元素移动到正确的位置。它将比 temp 大的元素向右移动一个位置，然后将 temp 插入到正确的位置。

for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
    arr[j] = arr[j - gap];
}
arr[j] = temp;

更新增量：将增量减半，以便进行下一轮的排序。

gap = Math.floor(gap / 2);

相比简单的插入排序，希尔排序通过这种逐步减少增量的方式，减少了数据移动的范围，使得最终插入排序时数据已经接近有序，从而提高了排序效率。希尔排序的代码主要分为外层控制增量的循环和内层进行插入排序的过程，结合递减增量的方式让排序更快逼近有序状态。

希尔排序的时间复杂度通常介于 O(n^1.3) 和 O(n^2) 之间，具体取决于增量序列的选择。虽然不是最优排序算法，但其简单性和有效性使得它在某些场景下仍然具有应用价值。