pytest
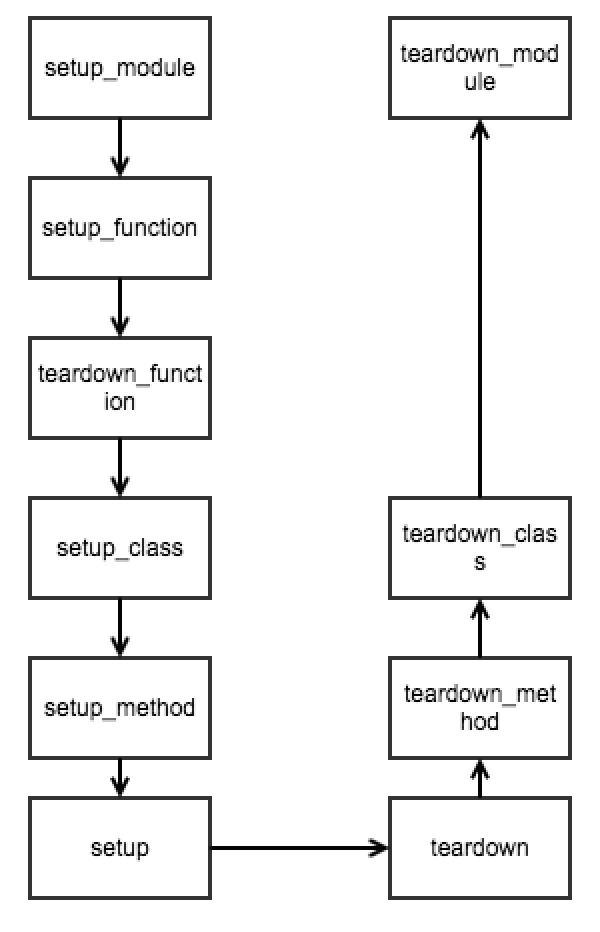为什么要有feature？ # python语法 生成器 ```python def fib(max): n, a, b = 0, 0, 1 while n < max: yield b a, b = b, a+b n += 1 for i in fib(6): print i ``` 装饰器 ```python def log(func): def wrapper(*args, **kw): print 'call %s():' % func.__name__ return func(*args, **kw) return wrapper @log def now(): print '2013-12-25' 相当于now=log(now) ``` ```python def f1(a, b, c=0, *args, **kw): print('a =', a, 'b =', b, 'c =', c, 'args =', args, 'kw =', kw) >>> f1(1, 2, 3, 'a', 'b', x=99) a = 1 b = 2 c = 3 args = ('a', 'b') kw = {'x': 99} ``` # 操作系统之流水线 1，从CS:IP指向内存单元读取指令，读取的指令进入指令缓冲器； 2，IP读取该指令长度，指向下一条指令； 3，执行程序。重复步骤一。 编译－》链接－》生成可执行文件。可执行文件装入内存，设置CS:IP入口
数据结构之排序
快排
时间常数最小
// s[l]=s[i]就是第一个坑
while i < j
// 从右向左找小于x的数来填s[i]
// 将s[j]填到s[i]中，s[j]就形成了一个新的坑
// 从左向右找第一个大于等于x的数来填s[j]
// 将s[i]填到s[j]中，s[i]就形成了一个新的坑
//退出时，j等于i。将x填到这个坑中
//递归调用
归并排序
通过先递归的分解数列，再合并数列就完成了归并排序。
数据库
Create：create database <database_name>。use <database_name>; create table <table_name> (字段设定列表);
Update：update <table_name> set username=’china’ where id=2;
Retrieve：select * from <table_name> where id=2;
Delete：delete from <table_name> where id=2;
表的设计
为了防止某张表被重复读取，取外键（算法：B+tree）。
一对一，多对多，一对多，多对一
redis：查找快，数据冗余
包括set,zset,list,hash,string这五种数据类型
读写分离一般都是结合Master/Slave模式使用，Master处理写请求，Slave处理读请求，这样做的好处是：
1、提高数据库的并发处理能力；
2、避免写请求锁表阻塞读请求；
3、避免单点，提高数据库的可用性；
而使用Redis作为DB前面的缓存，是为了减少对MySQL的压力，提高系统的处理效率。
二者解决的问题域不同，不存在谁替代谁。
一般高并发应用都是结合二者使用。
计算机网络
tcp udp socket
（tornado）
高等数学
欧拉公式
线性代数
最小二乘法的求解
概率论
朴素贝叶斯
（xgboost）
电磁波与电磁场
纪录道喜欢的题目
第7章平面电磁波
例7-8
海水的参数为
ϵ
r
=
80
\epsilon_r=80
ϵr=80，
μ
r
=
1
\mu_r=1
μr=1，
σ
=
4
S
\sigma=4S
σ=4S/m，频率为3kHz和30MHz的电磁波在海平面处（刚好在海平面下侧的海水中）的电场强度为1V/m，求
（1）电场强度衰减为1
μ
\mu
μV/m处的深度，应选择哪个频率进行潜水艇的水下通信；
（2）频率为3kHz的电磁波从海平面下侧向海水中传播的平均功率流密度。
解（1）当
f
f
f=3kHz时，有
P168 有耗媒质中的传播常数$\bar k=\omega\sqrt{\mu \bar\epsilon}$为一复数，而且$\bar k=\beta-j\alpha$ $\therefore \bar k^2=(\beta-j\alpha)^2=\omega^2\mu\bar \epsilon$ 将$\bar \epsilon=\epsilon - j\dfrac{\sigma}{\omega}$代入上式得$(\beta-j\alpha)^2=\omega^2\mu(\epsilon-j\dfrac{\sigma}{\omega})$ 展开得$\beta^2-\alpha^2- j2\beta\alpha=\omega^2\mu\epsilon- j\omega\mu\sigma$ $\Rightarrow \begin{cases}\beta^2-\alpha^2=\omega^2\mu\epsilon \\ 2\beta\alpha=\omega\mu\sigma \end{cases}\Rightarrow \alpha=\omega\sqrt{\dfrac{\mu\epsilon}{2}\left[\sqrt{1+(\dfrac{\sigma}{\omega\epsilon})^2}-1\right]}$
P165 $\because$ 在无源有耗媒质中由于电磁场的存在(the existence of the electromagnetic field in a passive lossy medium)，会有传导电流密度存在，即$\vec{J_c}=\sigma\vec{E}$[公式由来](#current_density)
$\therefore\nabla*\vec{H}=\vec{J}+j\omega\epsilon\vec{E}=\sigma\vec{E}+j\omega\epsilon\vec{E}$。该等式右端第一项代表传导电流密度，第2项代表位移电流密度，二者模之比即为$\dfrac{\sigma}{\omega\epsilon}$。由此可见，$\dfrac{\sigma}{\omega\epsilon}$值的大小表明了传导电流密度与位移电流密度的相对大小。$\dfrac{\sigma}{\omega\epsilon}<10^{-2}，为电解质$；$10^{-2}<\dfrac{\sigma}{\omega\epsilon}<10^2，为不良导体$；$10^2<\dfrac{\sigma}{\omega\epsilon}，为良导体$
P66 电流密度矢量(the vector of current density) $$|\vec{J}|=\dfrac{dI}{dS}$$ $\vec{J}$的方向规定为正电荷运动的方向，单位为$A/m^2$
根据试验，对于大部分导电媒质，其中电流密度与电场强度的关系可表示为$$\vec{J}=\sigma\vec{E}＝\sigma \dfrac{dIR}{dl} $$式中，$\sigma$称为导电媒质的电导率，单位为S/m。其倒数是导体的电阻率，即$\dfrac{1}{\sigma}$，单位为$\Omega\bullet m$。
hadoop
并行化的理念存在于计算机的方方面面
硬件上同一时刻使用所有的门电路
spark
对于一些复杂任务map reduce编程比较复杂，在不同的阶段之间产生大量的IO操作。因此出现了内存计算
由于hadoop的计算速度不够出现的，基于hadoop
在内存之中实现内存的共享，大大的提高内存的性能，从几十分钟缩短到几秒钟
python web框架之间的关系
一、整体设计方面
首先，两者都是非常优秀的框架。整体来讲，两者设计的哲学是区别最大的地方。
Django提供一站式的解决方案，从模板、ORM、Session、Authentication等等都分配好了，连app划分都做好了，总之，为你做尽量多的事情，而且还有一个killer级的特性，就是它的admin，配合django-suit，后台就出来了，其实最初Django就是由在新闻发布公司工作的人设计的。
Flask只提供了一些核心功能，非常简洁优雅。它是一个微框架，其他的由扩展提供，但它的blueprint使它也能够很方便的进行水平扩展。
Tornado不仅仅是一个WEB框架，它还完整地实现了异步非阻塞HTTP服务器和客户端，在此基础上提供WEB服务。
二、路由设计
Django的路由设计是采用集中处理的方法，利用正则匹配。Flask也能这么做，但更多的是使用装饰器的形式，这个有优点也有缺点，优点是读源码时看到函数就知道怎么用的，缺点是一旦源码比较长，你要查路由就不太方便了，但这也促使你去思考如何更合理的安排代码。
三、应用模块化设计
Django的模块化是集成在命令里的，也就是说一开始Django的目标就是为以后玩大了做准备的。每个都是一个独立的模块，为以后的复用提供了便利。
Flask通过Blueprint来提供模块化，自己对项目结构划分成不同的模块进行组织。
四、配置
Django的配置主要还是靠settings.py来做，当然为了Development和Production环境分离，还有一些方法来处理配置。
Flask的配置很灵活，有多种方法配置，不同环境的配置也非常方便。
五、文档
两者都提供了详尽的文档，Flask的文档风格很受我个人喜好，Django的文档也非常优秀。
六、社区
Django社区很大，各种插件很齐全，大部分情况下你都能找到你想要的。
Flask起步晚，但社区也不小，之前有一次看在github上的star数，两个相差并不远，说明越来越多的人关注它，虽然插件没那么全，但常用的还都是有的，而且质量都比较高。
最后再次说一下，两个都是非常优秀的框架，很多时候选用这些框架是根据实际项目侧重不同来选的。
xgboost
XGBoot是设计为高效、灵活、可移植的优化分布式梯度 Boosting库。它实现了 Gradient Boosting 框架下的机器学习算法。XGBoost通过提供并行树Boosting（也被称为GBDT、GBM），以一种快速且准确的方式解决了许多数据科学问题。相同的代码可以运行在大型分布式环境如Hadoop、SGE、MP上。它类似于梯度上升框架，但是更加高效。它兼具线性模型求解器和树学习算法。
XGBoot至少比现有的梯度上升实现有至少10倍的提升，同时还提供了多种目标函数，包括回归、分类和排序。由于它在预测性能上的强大，XGBoot成为很多比赛的理想选择，其还具有做交叉验证和发现关键变量的额外功能。
值得注意的是：XGBoost仅适用于数值型向量，因此在使用时需要将所有其他形式的数据转换为数值型向量；在优化模型时，这个算法还有非常多的参数需要调整。
参考文献：
《xgboost导读和实战》
java不适合开发游戏
java开发游戏性能和效率差，开发一些小游戏还可以，远标老师讲过java面向对象，所有方法都是封装在类里的，要调用方法就得实例类，而游戏主要侧重的是逻辑
对象就像是很多功能的机器，但是我的游戏逻辑只要每台机器的其中一个功能，但要用的话必须把这一整台机器制造出来。这就是面向对象的缺陷吧
而c是面向过程的可以更加灵活地设计过程逻辑，少去很多多余东西，大大提高性能
java的长处就是利用各种现存的类包，达到复用的效果，大大提高开发效率，
当然java也可以只针对逻辑来设计类，但那不是java的长处，没有多大的意义
斐波那契堆
转自http://blog.csdn.net/mishifangxiangdefeng/article/details/7823588
一、综述
1，斐波那契堆
斐波那契堆是可合并堆
在不涉及删除的操作（除去EXTRACT和DELETE）中，操作仅需O(1)的平摊运行时间。
当EXTRACT和DELETE的操作数目减小时斐波那契堆能得到较好的运行效率。
斐波那契堆不能有效地支持SEARCH操作。
为什么？用于解决诸如最小生成树和寻找单源最短路径等问题的快速算法都要用到斐波那契堆。
2，斐波那契堆结构
斐波那契堆由一组最小堆构成，这些最小堆是有根的无序树。
结点结构：
key: 关键字，作为排序、判断结点大小的标准
left、right: 用于维护双链表，所有的根结点形成一个双链表，每个结点的孩子们形成双链表
parent、child: 维护父子关系
mark: 这个域与维护结构无关，只有与具体的算法策略有关，不在这里讲
degree: 纪录该结点有几个孩子
斐波那契堆
n: 堆中结点的个数
min: 批量最小的结点
3，可合并堆
引理19.1中给出的二项树的性质对无序二项树仍然成立
有n个结点FibHeap，结点的最大度数D(n) = logn(向下取整)
将合并堆的操作尽可能地拖后
4，最大度数的界
在一个包含n个结点的斐波那契堆中，结点的最大度数D(n)为O(lgn)
二、理解
1，延迟合并操作
FIB-HEAP-INSERT和FIB-HEAP-UNION只是最基础的链表合入操作，因为合并操作要尽可能地拖后
FIB-HEAP-EXTRACT-MIN除了要完成本职工作外，还要作合并调整
2，合并调整操作
CONSOLIDATE是作合作并调整的函数
它将度数相同的根链接起来，直到对应每个度数至多只有一个根
遍历每个根结点去判断，如果两个根结点的度是一样的，让大的结点作为小的结点的孩子
3，mark的作用
为了防止堆太宽，需要策略来调整堆，使根结点成为别的根结点的孩子，该策略就是CONSOLIDATE
同理，为了防止堆太深，也需要有相应的策略去调整，在适当的时候，把某个结点的孩子变为根
这一策略就是CUT和CASCADING-CUT，mark在实现这一策略的过程中起到辅助作用。
原理：当一个非根结点被切掉了2个孩子，就把它升为根结点
在删除一个结点时，怎么区分是第一个被删除的孩子，还是第二个？此时需要用mark来标记
4，P300那句话
因为翻译不好，严重影响理解
一旦第二个孩子也失掉后，x与其父结点之间的联系就被切断了，并成为一个新根。
原文：As soon as the second child has been lost, we cut x from its parent, making it a new root.
三、改进
1，命名
mark的命名不能体现它的作用，影响理解，如果换一个好一点的名字，就不用那么大段的文字去说明
外部函数不需要FIB-HEAP-这样的前缀，因为本来就是为它写的接口
内部函数的名字要说明函数的作用，因为内部函数是被自己调用的，不要给自己添麻烦
2，分解函数
提取了一些对双链表的常用操作
3，合并函数
CUT和CASCADING-CUT合并成一个函数，因为它们其实是一个功能，就是根据策略把孩子结点升为根结点
4，参数和返回值
CUT和CASCADING-CUT中的x和y是父子关系，而且重点是子，父是只为了方便处理，不需要作为参数传进来，在函数里面重新获取一个就可以了。多传一个函数，就一个出错源
对于带参数的函数，增加一返回值。用于告知调用者是否成功，或什么原因导致失败
5，功能
FIB-HEAP-DECREASE-KEY和FIB-HEAP-DELETE这两个函数作用不大。
因为它们的入参是node*。要想调用这两个函数，就必须先获取目标结点的指针。
可是没有一个接口返回指向结点的指针，怎么找到我的目标结点的指针呢？
调用者必须自己在创建结点后保持这个结点，这样不合理
四、代码
1，FibHeap.h
2，FibHeap.cpp
3，测试用例
五、习题
20.1斐波那契堆
20.2可合并堆
20.2-1
20.2-4
McGee和FibHeap的区别在于合并的时机。
Fibheap认为合并调整应该尽量地推迟，而McGee则在每次堆中结点有增加的时候就作合并调整。
个人认为，合并调整操作的意义是防止堆过宽而影响性能。但是从算法过程上看，根结点的个数多少不会影响INSERT和UNION的性能，因此没有必要。
比较认可FibHeap的做法。
20.3减小一个关键字与删除一个结点
20.3-1
根据P300的描述，只有非根结点才可能被打上标记，如果根结点有标记，一定是它是非根结点的时候打上标记，然后被移到根结点的位置。
把结点移至根结点是通过上面代码中的函数addNodeToRootList和addListToRootList完成的，目标缩小至这两个函数周围
让根结点成为有标记结点，须满足以下两个条件
（1）调用这两个函数前，该结点是非根结点
（2）调用后没有清标记
结论：x是pMinData的孩子，根据P300的步骤被打上标记后，执行extract()时又成为根结点
20.4最大度的界
六、思考题
20-1删除的另一种实现
把FIB-HEAP-DELETE中的两个函数展开，再和PISANO-DELETE对比，并附上x不是min[H]的假设，可以发现这两个函数执行的操作基本上是一样的，区别在于
（1）PISANO-DELETE中去掉了FIB-HEAP-DELETE中多余的判断，不影响效率
（2）FIB-HEAP-DELETE在删掉结点之后有合并调整的动作
a)add x’s child list to the root list of H的时间不是O(1)，因为每个child都有一个pParent指针，必须依次修改每个child的指针
20-2其它斐波那契堆的操作
a)
（1）k < key[x]的情况，直接调用FIB-HEAP-DECREASE-KEY
（2）k = key[x]的情况，不用处理
（3）k > key[x]的情况，交换它与它孩子的内容，但是指针保持不变，直到符合最小堆的情况，时间与堆的深度有关
b)
以我有限的智商，只能想到执行min(r, n[H])次EXTRACT
3178
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
