边缘检测(Edge Detection)和极值点检测(Blod Detection)相关知识

a.一阶导数的极值

图像的一阶导数极值一般是求图像中物体的边缘，而对于图像极值点的求法就是对二维离散点求导（这里的导数是二元导数，有方向，有大小的矢量，一般称为梯度（方向指向数值增量最快的方向），因此在图像处理中，求导数一般称为求梯度）。

对于二维离散图像求梯度的方法 就是求x,y方向的微分：

$G(x,y)=dx(i,j)+dy(i,j)$, 其中 $dx(i,j)=I(i+1,j)-I(i,j);dy(i,j)=I(i,j+1)-I(i,j)$

或者用中值差分法：$dx(i,j)=(I(i+1,j)-I(i,j))/2;dy(i,j)=(I(i,j+1)-I(i,j))/2$

对于一幅二维数字图像f(x,y),它的二维梯度可以表示成：${\nabla }^F=(\frac{\partial }{\partial x}\frac{\partial }{\partial y})$
梯度算子定义为：$G(x,y)=\sqrt{({\nabla }_{x}f(x,y){)}^2+({\nabla }_{y}f(x,y){)}^2}$。为了简化表示，可以写成$G(x,y)=|{\nabla }_{x}f(x,y)|+|{\nabla }_{y}f(x,y)|$
常用的算子（图像的梯度可以用一阶导数和二阶偏导，但图像是以矩阵的形式存储的，对它进行梯度操作，需要模板（Roberts、Prewitt、Sobel、Lapacian算子）对原图像进行卷积）

b、二阶导数的过零点

二阶导数算子实际就是Laplacian算子，它定义为两个方向一阶梯度向量算子的内积，一般用$\Delta$表示拉普拉斯算子。

$\Delta ={\nabla }^2=[\frac{{\partial }^2}{{\partial }^{2}x}\frac{{\partial }^2}{{\partial }^{2}y}][\frac{{\partial }^2}{{\partial }^{2}x}\frac{{\partial }^2}{{\partial }^{2}y}{]}^T=\frac{{\partial }^2}{{\partial }^{2}x}+\frac{{\partial }^2}{{\partial }^{2}y}$

一阶导数：

二阶导数（拉普拉斯算子），这里是感兴趣的点是点n的二阶导数，因此求二阶导需要变换一下：

对于图像矩阵通过拉普拉斯模板求二级导数：

因此，对应的卷积模板通常为

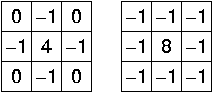
拉普拉斯算子是图像二阶空间导数的二维各向同性测度。拉普拉斯变化突出了快速强度变化区域，因此常用于边缘检测。由于拉普拉斯算子是通过对图像进行微分操作实现边缘检测，对于图像噪声和离散点比较敏感。因此，拉普拉斯通常被应用于首先经过高斯卷积滤波进行降噪处理过的图像，以提高算子对噪声和离散点的鲁棒性，于是，引入了高斯拉普拉斯算子。

拉普拉斯高斯（LOG：Laplacian of Gaussian）：

但是正如上边所说，laplacian 算子对噪声和离散点比较敏感，因此需要先进行高斯滤波。由于laplacian算子可以用卷积表示，而卷积运算具有关联性，因此可以先对高斯平滑滤波器与laplacian滤波器进行卷积，然后用混合滤波器对图像进行卷积。
好处：
（1）两个滤波器矩阵较小，先卷积可以减少计算量。
（2）对图像只需进行一次卷积运算。

用公式说明：

二维高斯函数可以表示为：$G_{\sigma }(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}$

对滤波后的图像作拉普拉斯变换就相当于先对高斯滤波作拉普拉斯（作卷积），再对图像作卷积：$\Delta [G_{\sigma }(x,y)\ast f(x,y)]=[\Delta G_{\sigma }(x,y)]\ast f(x,y)=LoG\ast f(x,y)$（卷积的微分性质得到）

卷积性质如下：$g(t)=h(t)\ast f(t)=\int f(\tau )h(t-\tau )d\tau$ \
$\frac{d}{dt}g(t)=\frac{d}{dt}[h(t)\ast f(t)]=\frac{d}{dt}\int f(\tau )h(t-\tau )d\tau =\int f(\tau )\frac{d}{dt}h(t-\tau )d\tau =\int h(\tau )\frac{d}{dt}f(t-\tau )d\tau =h^{‘}(t)\ast f(t)=f^{‘}(t)\ast h(t)$

从上面的公式可以看出对二维数字图像的拉普拉斯变化可以先转化成对高斯滤波的拉普拉斯变换，然后对图像卷积，。

我们计算拉普拉斯高斯算子(LoG),这里暂时忽略系数$\frac{1}{2\pi {\sigma }^2}$ :
$\Delta G_{\sigma }(x,y)=\frac{{\partial }^2}{\partial x^2}{G}_{\sigma }(x,y)+\frac{{\partial }^2}{\partial y^2}{G}_{\sigma }(x,y)$
$\frac{\partial }{\partial x}{G}_{\sigma }(x,y)=\frac{\partial }{\partial x}{e}^{\frac{-(x^2+y^2)}{2{\sigma }^2}}=-\frac{x}{{\sigma }^2}{e}^{\frac{-(x^2+y^2)}{2{\sigma }^2}}$
$\frac{{\partial }^2}{\partial x^2}{G}_{\sigma }(x,y)=\frac{x^2-{\sigma }^2}{{\sigma }^4}{e}^{\frac{-(x^2+y^2)}{2{\sigma }^2}}$

同理可以求得：

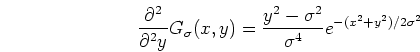
因此我们可以得到拉普拉斯高斯算子（这里忽略了$\frac{1}{2\pi {\sigma }^2}$）：

图片展示了高斯函数及其各阶导数曲线：

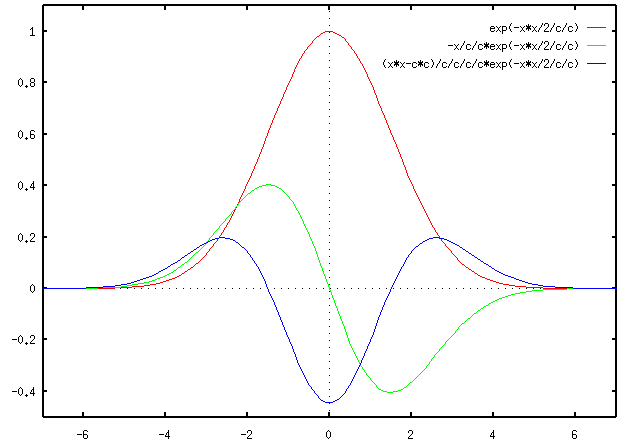
2维的LoG算子可以通过任何一个方形核逼近，只要能够确保卷积核的元素和为0，如下表示为一个5x5的卷积核

LoG与图像卷积时，当相应的绝对值超过制定阈值时，那么该点就是被检测出来的极值点, 一般设置为1，否则为0。

差分高斯算子（DOG: Difference of Gaussian)

与高斯拉普拉斯算子一样，差分算子同样需要先对图像进行高斯卷积滤波。

二维高斯函数：$G_{\sigma }(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}$

我们得到不同$\sigma$ 滤波后的图像函数：$g_1(x,y)=G_{k\sigma }(x,y)\ast f(x,y)$ ;$g_2(x,y)=G_{\sigma }(x,y)\ast f(x,y)$

因此差分高斯处理可以写成：$g_1(x,y)-g_2(x,y)=G(x,y,k\sigma )\ast f(x,y)-G_{(}x,y,\sigma )\ast f(x,y)=DoG\ast f(x,y)$

差分算子可以写成：$DoG=G(x,y,k\sigma )-G(x,y,\sigma )=\frac{1}{2\pi }(\frac{1}{k^2{\sigma }^2}{e}^{-\frac{(x^2+y^2)}{2k^2{\sigma }^2}}-\frac{1}{{\sigma }^2}{e}^{-\frac{(x^2+y^2)}{2{\sigma }^2}})$

由上边的拉普拉斯高斯算子（LoG）公式:

我们可以得到：$\frac{\partial G}{\partial \sigma }=\sigma LoG=\sigma \Delta G=\sigma {\nabla }^{2}G;\frac{\partial G}{\partial \sigma }\approx \frac{G(x,y,k\sigma )-G(x,y,\sigma )}{k\sigma -\sigma }$

故 $G(x,y,k\sigma )-G(x,y,\sigma )=DoG\approx (k-1){\sigma }^2{\nabla }^{2}G=\Delta$

其中$K-1$为常数，不影响极值点的检测，LoG与DoG对比图如下：

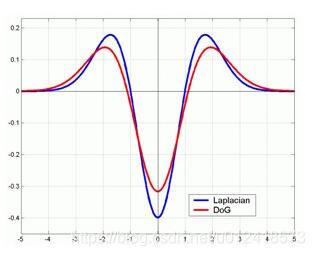边缘检测(Edge Detection)和极值点检测(Bold Detection):二阶微分算子在边缘出为一过零点，而且过零点两边的最大值和最小值的差值较大。

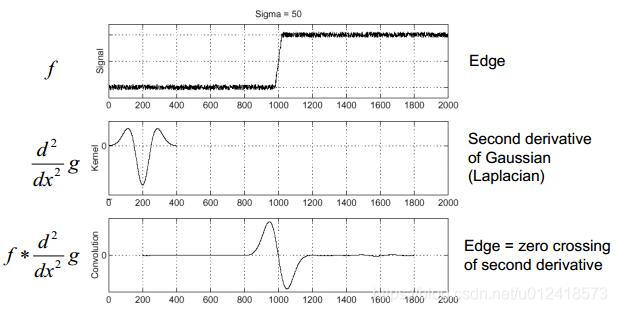下图是边缘和极值点位置处算子的响应：
检测流程：
（1）对原图像进行LoG或DoG卷积滤波。
（2）检测卷积后图像中的过零点或极值点。
（3）如果是边缘检测，则对过零点进行阈值化(过零点两边的最大值和最小值之间的差值要大于某个阈值)；如果是极值点检测，则极值点的LoG或DoG响应应该大于某个阈值。