某次计算机仿真比赛之前看到到这个东西,想试一试,于是用c#实现了一下,结果令人很震撼!
看看效果:



先介绍以下元胞自动机的原理:
细胞自动机
(Cellular Automata,
简称
CA)
、也称为元胞自动机或者格点自动机。它是一个空间离散、时间离散、状态离散的模型。形象地说,它是由大量简单的、具有局部相互作用的基本构件
(
细胞
)
所构成的。在每一仿真时钟内,各个细胞按照自身及与它直接相邻的细胞在这一时刻的状态和一定的局部规则来确定自己在下一仿真时钟的状态。
细胞自动机起源于生物体发育中细胞的自我复制。 20 世纪 50 年代初,现代计算机的创始人冯 · 诺依曼 (von Neumann) 曾希望通过特定的程序在计算机上实现类似于生物发育中细胞的自我复制。由于当时电子管计算机的限制,他提出了一种简单的模式:把一个长方形平面划分为若干格网格.每一个格点表示一个细胞或系统的基元。他们的状态赋值为 0 或 1 在事先设定的规则下,细胞的演化就可以用网格中的空格或实格的变动来描述.这就是细胞自动机的雏形。在 von Neumann 逝世之后长达十多年的时间里,这一开创性的工作几乎完全停止了,至到 1970 年剑桥大学的 John H. Conway 编制了一个名为“生命的游戏” 〔TheGame of Life) 的程序 , 并由 《 科学美国人 》 的数学游戏专栏介绍到全世界 , 才使 CA 引起了人们的广泛关注与重视。
再来说说生命的游戏,先看程序界面:
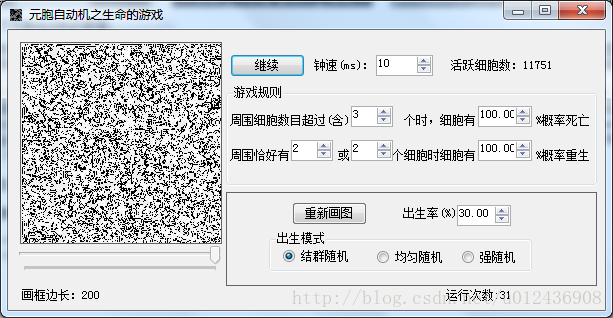
这里是以屏幕上每个像素代表一个细胞,细胞有生和死两种状态。最原始的规则是
细胞自动机起源于生物体发育中细胞的自我复制。 20 世纪 50 年代初,现代计算机的创始人冯 · 诺依曼 (von Neumann) 曾希望通过特定的程序在计算机上实现类似于生物发育中细胞的自我复制。由于当时电子管计算机的限制,他提出了一种简单的模式:把一个长方形平面划分为若干格网格.每一个格点表示一个细胞或系统的基元。他们的状态赋值为 0 或 1 在事先设定的规则下,细胞的演化就可以用网格中的空格或实格的变动来描述.这就是细胞自动机的雏形。在 von Neumann 逝世之后长达十多年的时间里,这一开创性的工作几乎完全停止了,至到 1970 年剑桥大学的 John H. Conway 编制了一个名为“生命的游戏” 〔TheGame of Life) 的程序 , 并由 《 科学美国人 》 的数学游戏专栏介绍到全世界 , 才使 CA 引起了人们的广泛关注与重视。
再来说说生命的游戏,先看程序界面:

这里是以屏幕上每个像素代表一个细胞,细胞有生和死两种状态。最原始的规则是
-
一个活着的细胞如果周围有超过三个活着的邻居则死去;
-
一个死去的细胞只有在刚好有两个活着的邻居才重生;

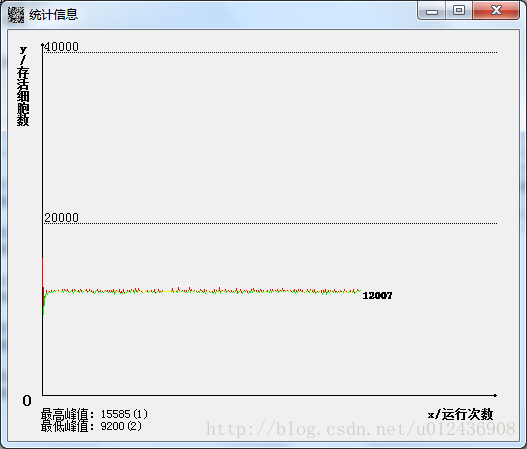
运行是还可以调整参数,会影响到细胞的数目变化,这里就不一一列举了。下面来看几个比较极端的例子:
运行后将死亡率降为0,调整重生数目让细胞铺满所有单元;
然后将出生率降为0;
调整参数:当细胞数目超过4个时,死亡率为100%;(这时就只剩下4个角的四个细胞存在了)
接着讲死亡率降为0,出生率加满100%,改变出生规则为1个或n个,你将看到无比美妙的图案。图的样式随n的不同而不同,中途可以继续改变参数,图案将千变万化。
分形魅力尽显于此!!
程序及源代码: 点此下载





运行后将死亡率降为0,调整重生数目让细胞铺满所有单元;
然后将出生率降为0;
调整参数:当细胞数目超过4个时,死亡率为100%;(这时就只剩下4个角的四个细胞存在了)
接着讲死亡率降为0,出生率加满100%,改变出生规则为1个或n个,你将看到无比美妙的图案。图的样式随n的不同而不同,中途可以继续改变参数,图案将千变万化。
分形魅力尽显于此!!
程序及源代码: 点此下载












 本文介绍了元胞自动机的基本原理及其应用实例——生命的游戏。通过简单规则,生成了令人震撼的视觉效果。探索不同的参数调整,展示了生命的游戏如何创造多样化的图案与分形魅力。
本文介绍了元胞自动机的基本原理及其应用实例——生命的游戏。通过简单规则,生成了令人震撼的视觉效果。探索不同的参数调整,展示了生命的游戏如何创造多样化的图案与分形魅力。

















 399
399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








