使用递归解汉诺塔

使用递归解汉诺塔

最近接触了好几个需要用递归来处理的问题，为了更好的理解递归，翻看了一些关于递归的资料，发现很多递归的资料都是以汉诺塔作为例子来进行讲解，所以打算写篇笔记来整理一下关于使用递归解汉诺塔的方法。

关于递归

很多人都听过这样一个故事：

从前有座山，山里有座庙，庙里有个和尚在讲故事，他讲的故事是：从前有座山，山里有座庙，庙里有个和尚在讲故事，他讲的故事是 ……

这个无限循环的故事其实就是一个递归的过程，不过在程序设计中的递归通常是指程序直接或间接调用自身的过程。

要使用递归解决问题，所要解决的问题需要满足两个条件：

1. 问题的求解过程必须直接或间接的调用问题本身。
2. 在递归过程中，达到一定的边界条件后，问题不再需要调用自身（也就是转为非递归状态）。如果不满足该条件，递归会无限进行下去。

下面分析解汉诺塔的过程看是否符合这两个条件。

汉诺塔的规则

在解汉诺塔前先说明下汉诺塔的规则，汉诺塔的规则有如下几条：

1. 汉诺塔由 3 个柱子和 N 个圆盘组成
2. 初始时，N 个圆盘全部在其中的一个柱子上
3. N 个圆盘的大小全都不一样，且规定较小的圆盘必须要在大的圆盘上面。因此初始状态时，所有圆盘都是按照大小顺序，从上到下由小到大的方式堆叠在同一个柱子上的。
4. 解汉诺塔的最终目标，是将初始状态时在同一柱子上的 N 个圆盘全部移动到另一个柱子上。
5. 在移动圆盘时，只能移动每个柱子最上面的圆盘（根据规则 3 该圆盘同时也是该柱子上最小的）
6. 在移动圆盘时，一次只能移动一个圆盘，可以使用剩下的那个柱子作为移动中介。

解汉诺塔的方法

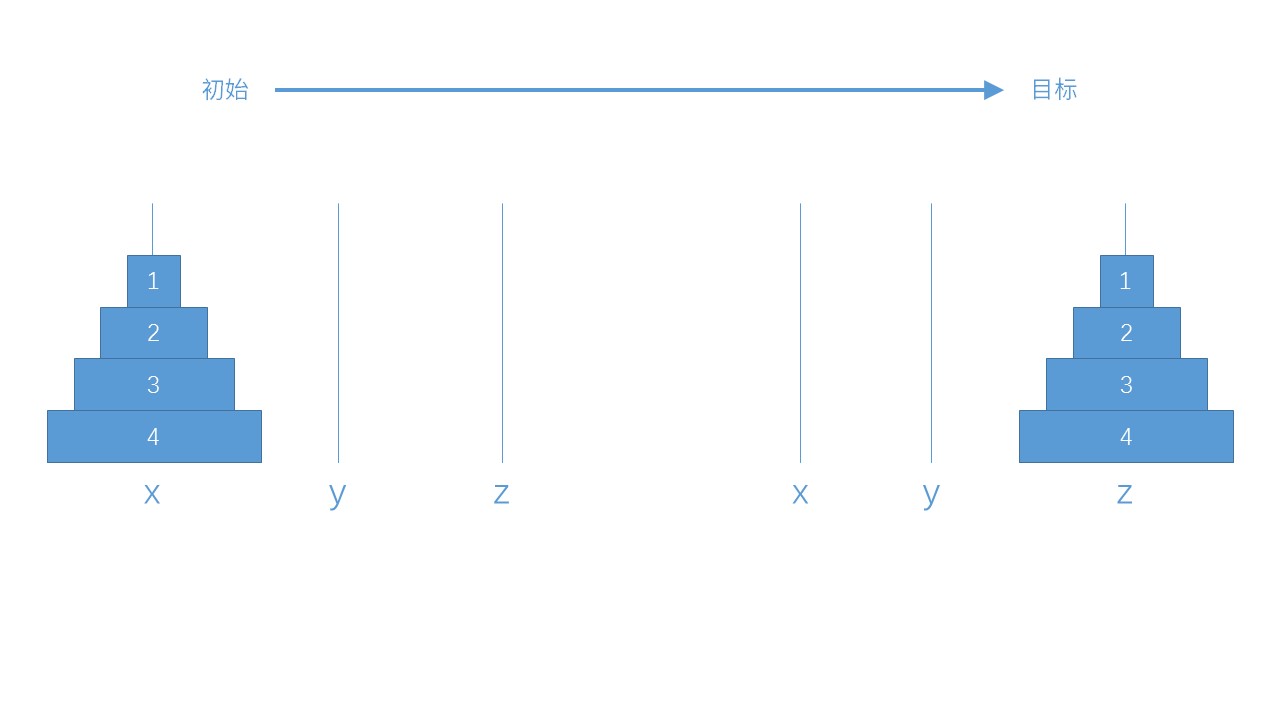
以一个有 4 个圆盘的汉诺塔为例，根据规则我们可以得到其初始状态和目标状态如下图所示：

我们的目标是将柱子 x 中的 4 个圆盘按顺序全部移动到柱子 z 上。乍看之下移动圆盘的步骤好像有多种方式，其实根据汉诺塔的规则，在由初始状态到目标状态的移动过程中必定要经过一个步骤。

首先根据规则 3 可知，要将柱子 x 上的圆盘移动到柱子 z，先要移动最大的圆盘 4 到柱子 z，此时汉诺塔的状态必须满足以下要求：

• 要移动 4，它必须是该柱子最上面的（即该柱子上最小的），所以柱子 x 上此时只有 4
• 要将 4 移动到柱子 z，根据规则 3 柱子 z 最上面的圆盘必须要大于 4 或为空，因为 4 是最大的，所以柱子 z 必须为空
• 由上面两条可知，余下的所有圆盘全部在剩余的柱子 y 上，并且根据规则 3 可知，它们都以大小顺序排列

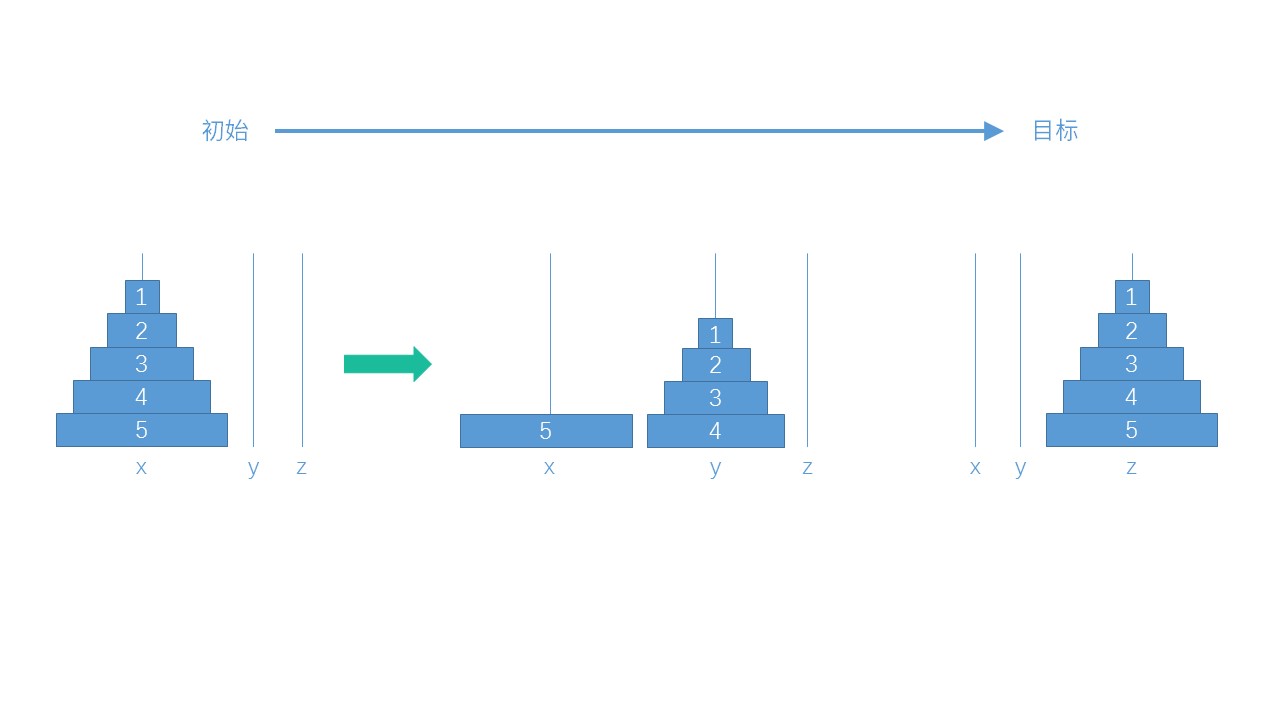
综合上面几点可以确定，在解汉诺塔时必定要经过移动最大圆盘 4 到目标柱子 z 这一状态，其示意图如下：

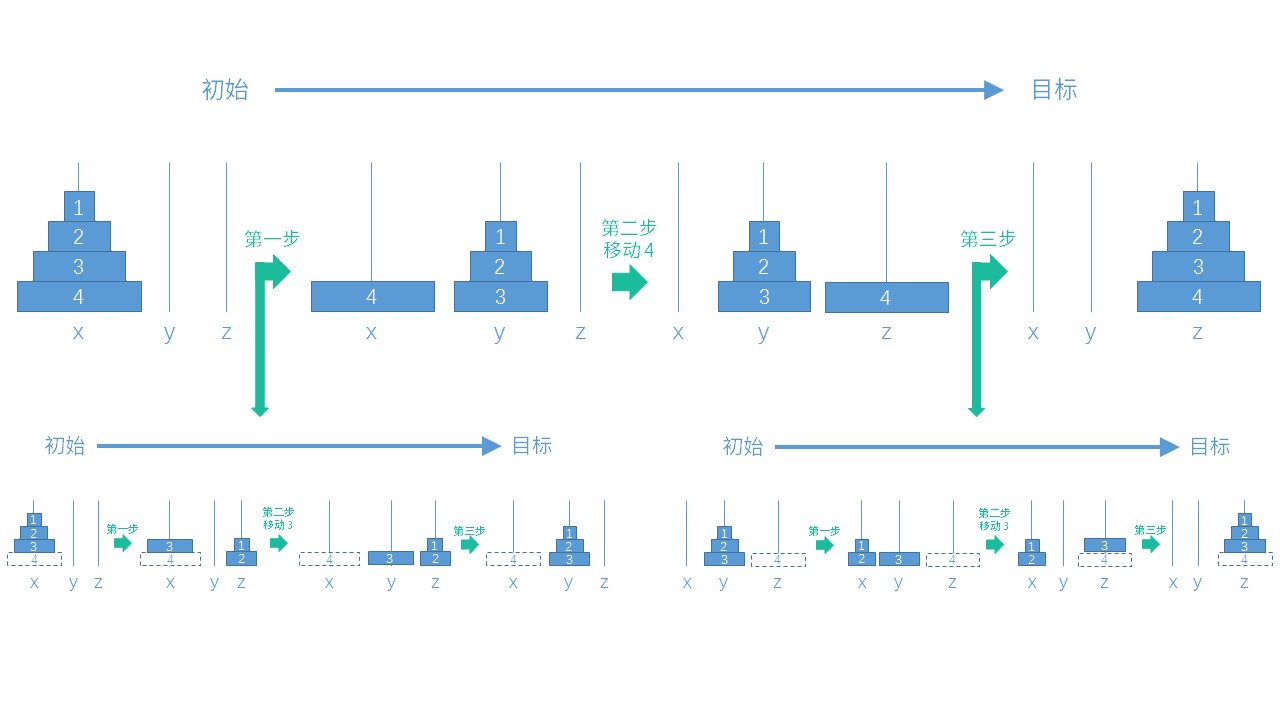
在由初始状态经过一系列操作到达这一状态后，只需移动最大盘 4 到 z，然后将 y 上所有圆盘移动到 z 即可达到目标状态，过程如下：

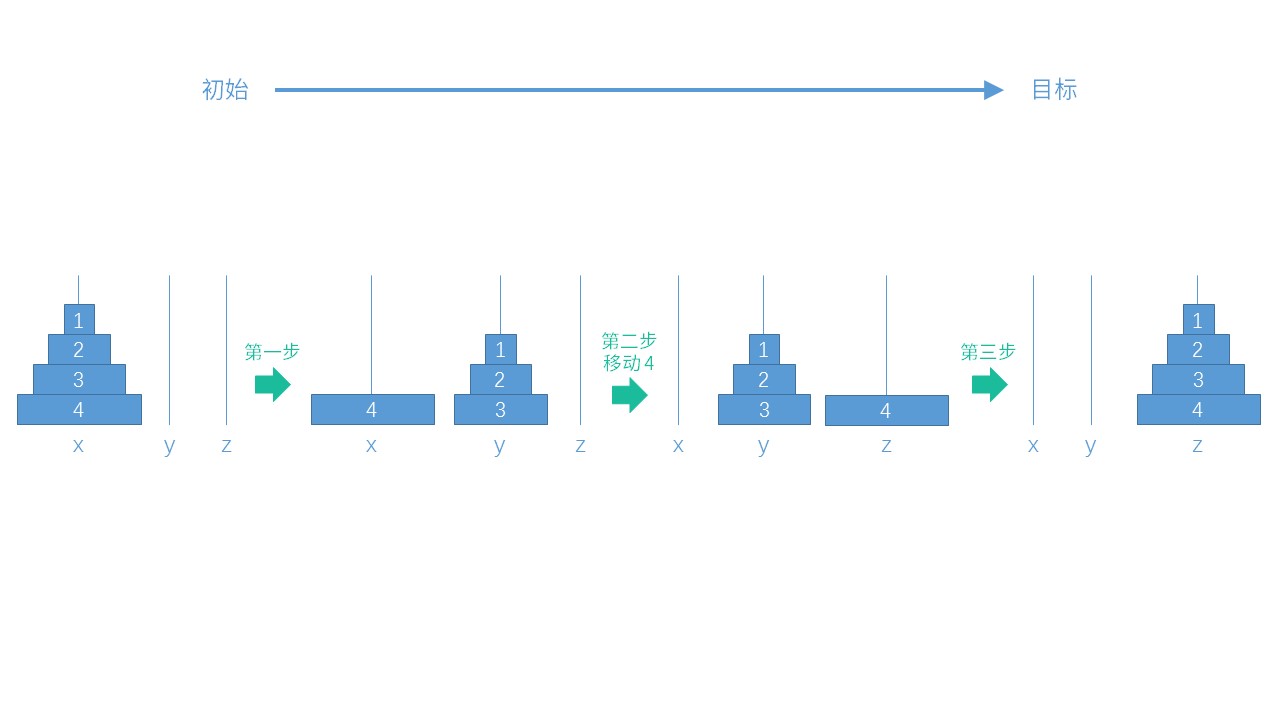
由此可将解汉诺塔的过程简单的概括为三步：

1. 将初始柱子上除最大盘之外的所有圆盘移动到非目标柱子（将柱子 x 上的 1 ~ 3 号圆盘移动到柱子 y 上）。
2. 将最大盘移动到目标柱子（将柱子 x 上的 4 号圆盘移动到柱子 z）
3. 将非目标柱子上的所有圆盘移动到目标柱子上（将柱子 y 上的 1 ~ 3 号圆盘移动到柱子 z 上）

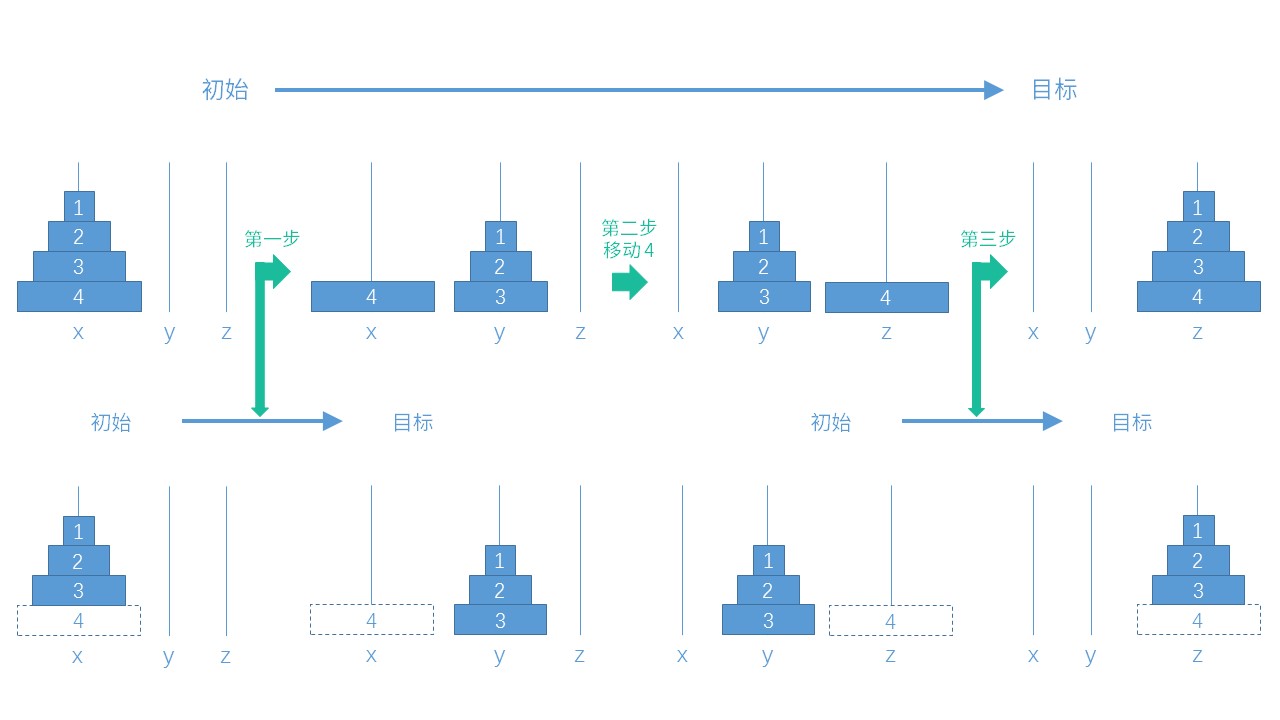
仔细观察上面的第一步和第三步，其实质都是把 1 ~ 3 号圆盘从一根柱子移动到另一根柱子，这完全可以看作是解一个有 3 个圆盘的汉诺塔：

对于解 3 个圆盘的汉诺塔，同样可以用之前归纳的三步解法，如图 ：

在解 3 个圆盘的汉诺塔三步过程中，第一步和第三步又需要解 2 个圆盘的汉诺塔，依次类推，之后还需