poyla计数问题

关于poyla计数，首先推荐两篇比较好的文章

2001-----符文杰《poyla原理及其应用》

2008-----陈瑜希《poyla计数法的应用》

在然后就是自己的学习笔记啦，据说《组合数学》一书当中讲得比较好，不过没看过，有机会找来看看

关于知识点嘛，下面给出一些：

Pólya原理是组合数学中，用来计算全部互异的组合状态的个数的一个十分高效、简便的工具。

在介绍polya定理之前，先介绍几个概念

      群：给定一个集合G={a,b,c,…}和集合G上的二元运算，并满足:
(a) 封闭性："a,bÎG, $cÎG,a＊b=c。
(b) 结合律："a,b,cÎG, (a＊b)＊c=a＊(b＊c)。
(c) 单位元：$eÎG,"aÎG, a＊e=e＊a=a。
(d) 逆元："aÎG,$bÎG, a＊b=b＊a=e，记b=a-1。
则称集合G在运算＊之下是一个群，简称G是群。一般a＊b简写为ab。          

       置换：n个元素1,2,…,n之间的一个置换 表示1被1到n中的某个数a1取代，2被1到n中的某个数a2取代，直到n被1到n中的某个数an取代，且a1,a2,…,an互不相同。

       置换群：置换群的元素是置换，运算是置换的连接。 

       循环：记 
称为n阶循环。每个置换都可以写若干互不相交的循环的乘积，两个循环(a1a2…an)和(b1b2…bn)互不相交是指ai!=bj, i,j=1,2,…,n。例如：

这样的表示是唯一的。置换的循环节数是上述表示中循环的个数。例如(13)(25)(4)的循环节数为3。

其实，polya定理是burnside引理的一种特殊情况。。。至于burnside引理，这就不详细探讨了。。。

下面直接给出polya定理的公式：

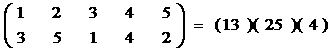
　  设G是p个对象的一个置换群，用m种颜色涂染p个对象，则不同染色方案为：

      L=1/|G|(m^c(g1)+m^c(g2)+...+m^c(gs))

     其中G={g₁,…g_s}   c(g_i )为置换g_i的循环节数(i=1…s)

好了，下面上一些题目

由于poyla定理实在是不好理解，所以先上一个裸题，本人天资愚钝，裸题也是看了两天才会做的，poyla定理更是理解了好几天，希望做后面的题能顺点，废话不说看题

 1.poyla定理直接套公式类型

poj2409

链接：http://poj.org/problem?id=2409

题解：这是本人在实习阶段写的一道题

这两道题都是很裸的polya定理题，而且代码几乎一样，所以把他们放到一起。。。

         至于polya定理的理论部分，可以看我的上一篇blog。。。

         这两道题：

         对于旋转的情况：共有n个置换，其中旋转k个位置的置换的循环节数为gcd(n,k)。——(|)证明如下
         对于翻转的情况：若n为奇数，则对称轴过一顶点和一边中点，n种置换，循环节长度n/2+1；若n为偶数，对称轴有两种，过两点和过两边中点，两者各有n/2种置换，前者          循环节长度为n/2+1，后者为n/2。

         总共有2*n个置换。

         这部分也很好理解。。。接下来我要来证明一下(|)。。。

          假设旋转k个位置，因为polya定理要求在置换后元素不变的情况下每种置换的循环节数，所以当他旋转到他原来的位置时，

          所经过的点数既是n的倍数，又是k的倍数，且是n和k的最小公倍数，即lcm(n,k)；

          因为每次旋k个位置，所以当前置换中循环的个数为lcm(n,k)/k；

          所以每个置换的循环节数=n/(lcm(n,k)/k)=gcd(n,k)。