CLRS 14.2如何扩张数据结构

14.2-1
对于MINIMUM、MAXIMUM 这种属于树的全局属性的可以直接修改（比如我们把哨兵结点的左右指针分别指向MINIMUM、MAXIMUM）。
插入时，我们比较插入的结点的关键字，若关键字小于MINIMUM所指关键字，则将指向MINIMUM的指针指向新的关键字，否则不变；对于删除操作，若删除了最小关键字，则将指向MINIMUM的指针指向被删除关键字的后继，因此若能在 $O(1)$ 时间求出后继，则可以在 $O(1)$ 的时间更改MINIMUM的指针。同理，我们可以更改MAXIMUM指针。

下面说明如何在 $O(1)$ 时间修改结点的SUCCESSOR、PREDECESSOR。注意到旋转操作并不会改变结点的SUCCESSOR、PREDECESSOR属性。所以会改变SUCCESSOR、PREDECESSOR属性的是插入和删除操作。
插入时，假设会插入到结点 $x$ 的左边，新结点为 $y$，那么需要修改：

x.predecessor.successor = y
y.predecessor = x.predecessor
y.successor = x
x.predecessor = y

插入到结点 $x$ 的右边也可以相似的修改。
综上可知可以在 $O(1)$ 的时间完成。

14.2-2
可以将黑高作为属性来维护，由定理 14.1 可知，我们计算结点的黑高只需要结点的左右孩子信息。结点 $x$ 的黑高是红孩子的黑高，是黑孩子黑高加1。
对于插入操作，情况 1 中，设着色之前 $\alpha,\beta,\gamma,\delta$ 的黑高都是 $k$，所以结点 $A,B,C,D$ 的黑高是 $k+1$。着色之后，只有结点 $C$ 的黑高变了，所以在RB-INSERT-FIXUP的第七行后加入z.p.p.bh=z.p.p.bh+1。情况 2 和 3 着色旋转之后黑高并不改变。
对于删除操作，情况 1 不改变黑高，情况 2 在RB-DELETE-FIXUP的第十行后面加上x.p.bh=x.bh即可，情况 3 也不改变黑高，情况 4 在RB-DELETE-FIXUP的第二十行后面加上x.p.bh=x.bh+1;x.p.p.bh=x.p.bh+1。

对于维护结点深度，我们的答案是否。

14.2-3
显然，对于任意结点 $x$ 的属性 $x.f=x.left.f\bigotimes x.a\bigotimes x.right.f$。
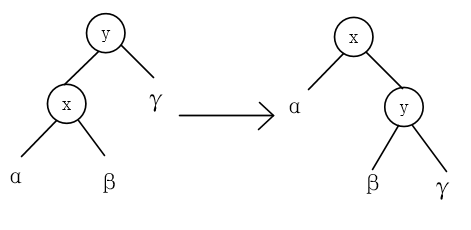
对于一次旋转，以右旋为例，子树$\alpha,\beta,\gamma$ 的属性并不用变，对于 $y$ 的 $f$ 域有 $y.f=\beta .f\bigotimes y.a\bigotimes \gamma .f$，对于 $x$ 的 $f$ 域有 $x.f=\alpha.f\bigotimes x.a\bigotimes y.f$。

14.2-4
在 $O(\lg n)$ 的时间找到最接近 $a$ 的元素，然后运行 $m$ 次SUCCESSOR即可。