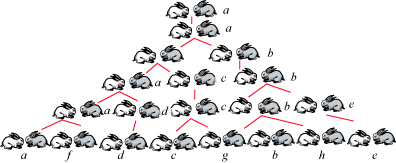
有这样一个有趣的“兔子问题”:“假定一对大兔子每月能生一对小兔子,且每对新生的小兔子经过一个月可以长成一对大兔子,具备繁殖能力,如果不发生死亡,且每次均生下一雌一雄,问一年后共有多少对兔子?”
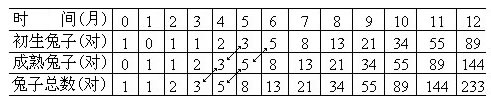
分析:第一个月兔子没有繁殖能力,所以还是一对;两个月后生下一对兔子,共有两对;三个月后,老兔子生下一对,小兔子还没有繁殖能力,所以一共是三对,以此类推,可以列出下表
表中1,1,2,3,5,8,13.....构成一个序列,这个数列有一个特点就是前两项之和等于后一项
数学函数定义:
实现:
public class Fibonacci {
//数组实现
public static void FbiArray(int n){
int i;
int []a = new int[n];
a[0] = 0;
a[1] = 1;
for (i = 2; i < n; i++){
a[i] = a[i - 1] + a[i - 2];
System.out.println(a[i]);
}
}
//递归实现
public static int Fbi(int n){
if (n < 2)








 本文探讨了著名的兔子问题,该问题涉及到斐波那契数列的运用。通过分析兔子的繁殖规律,展示了一个以1、1开始,每一项为前两项之和的数列,即斐波那契数列。文章还将讨论如何用数学函数来表示这一序列,并可能涉及其在实际问题中的实现方法。
本文探讨了著名的兔子问题,该问题涉及到斐波那契数列的运用。通过分析兔子的繁殖规律,展示了一个以1、1开始,每一项为前两项之和的数列,即斐波那契数列。文章还将讨论如何用数学函数来表示这一序列,并可能涉及其在实际问题中的实现方法。
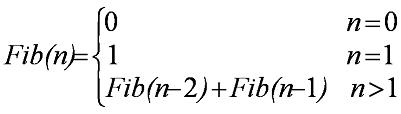
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1050
1050

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








