感知机 — Perceptron

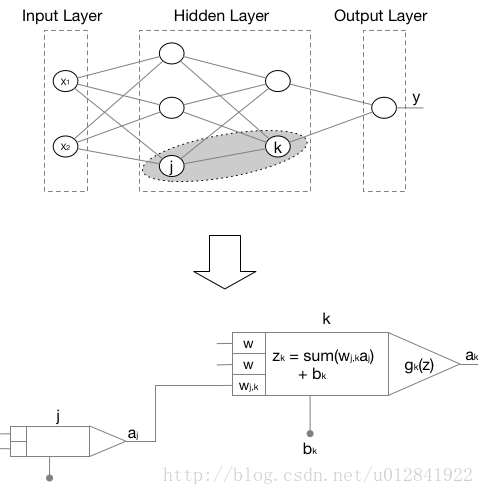
感知机是一种经典的神经网络算法，用于数据分类。其图形化展示如下图，相互连接的神经元$j$和神经元$k$做了放大处理，我们可以更清楚地了解感知机中每个神经元的计算逻辑。

其中，输入层$x_1$和$x_2$对应于一条有两个特征的数据，输出层$y$表示这条数据的标签（类别）。对于神经元$k$，接收它左侧三个神经元的输出，作为其输入。每一个输入配有一个权重$w_{jk}$，因此，神经元$k$接收的输入总和为$z_k=\sum _j{w}_{jk}{a}_j+b_k$。$g_k(z)$是神经元$k$的激活函数，其结果$a_k$作为神经元$k$的输出。即：
$$a_k=g_k(\sum _j{w}_{jk}{a}_j+b_k)$$

常见的激活函数有：

学习策略

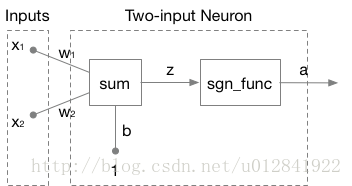
此处，我们以双输入单神经元感知机，$sgn\_func$作为激活函数为例开始讲解感知机的学习策略。如下图：

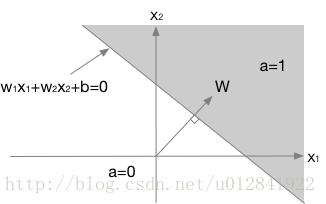
如上神经网络的输出定义为$a=sgn(W^{T}X+b)=sgn(w_1{x}_1+w_2{x}_2+b)$，决策边界定义为$z=W^{T}X+b=w_1{x}_1+w_2{x}_2+b=0$。其图形化展示如下：

其中，$W$为决策边界$W^{T}X+b=0$的法向量，始终垂直于决策边界。

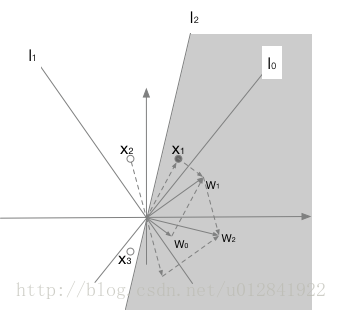
对于输入数据 { x 1 = [ 1 2 ] , y 1 = 1 } { x 2 = [ − 0.5 2 ] , y 2 = 0 } { x 3 = [ − 0.5 − 1 ] , y 3 = 0 } \{ x_1 = \begin{bmatrix} 1\\ 2 \end{bmatrix}, y_1 = 1\} \{ x_2 = \begin{bmatrix} -0.5\\ 2 \end{bmatrix}, y_2 = 0\} \{ x_3 = \begin{bmatrix} -0.5\\ -1 \end{bmatrix}, y_3 = 0\} {x1​=[12​],y1​=1}{x2​=[−0.52​],y2​=0}{x3​=[−0.5−1​],y3​=0}，下图中空心圆表示$y_i=0$，实心圆表示$y_i=1$。感知机的学习策略步骤如下：

1. 令$x_i^0=1$和$w_0=b$，我们随机初始化$W$构建感知机模型$l_0:W_{0}X=0$；
2. 在决策边界$l_0$的分类下，发现$x_1$被错误分类，即$y=1,a=0$。因此，参数更新公式有$W_1=W_0+x_1$（新的参数向量$W_1$使得新的决策边界$l_1$向$x_1$的方向旋转）；
3. 在决策边界$l_1$的分类下，发现$x_2$被错误分类，即$y=0,a=1$。因此，参数更新公式有$W_2=W_1-x_2$（新的参数向量$W_2$使得新的决策边界$l_2$向远离$x_2$的方向旋转）；
4. 在决策边界$l_2$的分类下，发现$x_1,x_2,x_3$均被正确分类，即$y=0,a=0$或$y=1,a=1$。因此，参数不再更新。

总结如上两种错误分类情况，即得统一的参数更新公式：
$$W^{new}=W^{old}+(y-a)X$$

此参数更新公式对于单隐层多神经元感知机同样适用，不过是$W$由向量变成了矩阵。

感知机的收敛性

由于 y − a ∈ { − 1 , 1 } y-a \in \{-1, 1\} y−a∈{−1,1}，可令$W(k+1)=W(k)+X^{\prime }(k)$。其中：
X ′ ( k ) ∈ { x 1 , x 2 , … , x m , − x 1 , − x 2 , … , − x m } X^{\prime}(k) \in \{ x_1, x_2, \dots, x_m, -x_1, -x_2, \dots, -x_m\} X′(k)∈{x1​,x2​,…,xm​,−x1​,−x2​,…,−xm​}

然后，我们假设感知机存在一个最终解$W^{\star }$，使得：
$$\begin{gathered} {W^{\star }}^T{x}_i>\delta >0|y=1 \\ {W^{\star }}^T{x}_i<-\delta <0|y=0 \end{gathered}$$

其中，$\delta$表示某可能很小的正数。结合$X^{\prime }(k)$的定义，得${W^{\star }}^T{X}^{\prime }(k)>\delta$。

$\mathcal{P}roof:$

初始化感知机参数$W(0)$为$0$，经过$k$次迭代后：
$$\begin{gathered} W(K)=X^{\prime }(0)+X^{\prime }(1)+X^{\prime }(2)+\cdots +X^{\prime }(k-1) \\ {W^{\star }}^{T}W(K)={W^{\star }}^T{X}^{\prime }(0)+{W^{\star }}^T{X}^{\prime }(1)+{W^{\star }}^T{X}^{\prime }(2)+\cdots +{W^{\star }}^T{X}^{\prime }(k-1) \end{gathered}$$

由于${W^{\star }}^T{X}^{\prime }(k)>\delta$，得${W^{\star }}^{T}W(K)>k\delta$。
$$\begin{gathered} ({W^{\star }}^{T}W(K){)}^2=(\Vert W^{\star }\Vert \Vert W(K)\Vert \cos \theta {)}^2\le {\Vert W^{\star }\Vert }^2{\Vert W(K)\Vert }^2 \\ {\Vert W(K)\Vert }^2\ge \frac{({W^{\star }}^{T}W(K){)}^2}{{\Vert W^{\star }\Vert }^2}>\frac{(k\delta {)}^2}{{\Vert W^{\star }\Vert }^2} \end{gathered}$$

接下来计算$\Vert W(K)\Vert$的上界：
$$\begin{array}{rl}& {\Vert W(K)\Vert }^2=W^T(K)W(K)\\ & =[W(K-1)+X^{\prime }(K-1){]}^T[W(K-1)+X^{\prime }(K-1)]\\ & =W^T(K-1)W(K-1)+2W^T(K-1)X^{\prime }(K-1)+{X^{\prime }}^T(K-1)X^{\prime }(K-1)\end{array}$$

对于$W(K-1)$，决策边界仍处于更新状态中。因此，必有数据被错误分类。如果$y=1,a=0$，$W^T(K-1)X^{\prime }(K-1)=W^T(K-1)X(K-1)\le 0$；如果$y=0,a=1$，$W^T(K-1)X^{\prime }(K-1)=-W^T(K-1)X(K-1)\le 0$（读者可以自行构建二维坐标系验证）。因此：
$${\Vert W(K)\Vert }^2\le \Vert W(K-1){\Vert }^2+\Vert X^{\prime }(K-1){\Vert }^2$$

重复迭代可得：
$${\Vert W(K)\Vert }^2\le \Vert X^{\prime }(0){\Vert }^2+\Vert X^{\prime }(1){\Vert }^2+\cdots +\Vert X^{\prime }(K-1){\Vert }^2$$
令$\Pi =\max (\Vert X^{\prime }(i){\Vert }^2)$，得：
$${\Vert W(K)\Vert }^2\le k\Pi$$

结合${\Vert W(K)\Vert }^2>\frac{(k\delta {)}^2}{{\Vert W^{\star }\Vert }^2}$，得：
$$\begin{gathered} \frac{(k\delta {)}^2}{{\Vert W^{\star }\Vert }^2}<{\Vert W(K)\Vert }^2\le k\Pi \\ k<\frac{\Pi {\Vert W^{\star }\Vert }^2}{{\delta }^2} \end{gathered}$$
得证感知机的学习能在有限次数内完成。

感知机的局限性

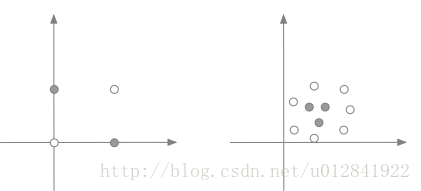
上面对单层神经元感知机学习策略的讲解和收敛性的证明都基于一个假设：数据是线性可分的。即存在一个超平面能将不同类的数据分隔开。然而，现实中的数据大多是非线性可分的，如下图：

而非线性数据可通过引入多层神经元处理。