算法分析入门详解之动态规划（一）

动态规划算法与分治法类似，其基本思想也是将待求解问题分成若干个小问题，但与分治法的不同之处在于经过分解后得到的问题不是互相独立的。也正是由于这个原因，大量子问题被重复计算，从而浪费了计算时间。我们知道，分治法的计算时间为指数级，而动态规划法的计算时间为多项式级（因为子问题的数量通常为多项式级的）。因此，动态规划法适用于解决最优化问题。通常有以下几个步骤：（1）分析最优结构；（2）递归定义；（3）计算最优值并求出最优解。

下面分析下矩阵连乘问题：

给定n个矩阵{A1, A2, A3, ..., A4},其中Ai与A(i+1)是可乘的，i=1,2,3,...,n-1,确定n个矩阵连乘积的最优计算次序。

矩阵A和B可乘的条件是A的列数等于B的行数，如A是p*q，B是q*m，则C=AB，C是p*m。由矩阵相乘定义可得经历一次矩阵相乘共需pqm次乘法。

（1）我们首先分析矩阵连乘问题的最优结构：

为方便书写，将矩阵连乘积Ai*Ai+1*...*Aj记为A[i:j]。我们可这样想，A[1:n]的计算可分为A[1:k]*A[k+1:n]，1<=k<n。这样我们就需要计算A[1:k]和A[k+1:n]，由此我们可以继续将两个子问题分解下去，知道每个子问题只剩下一个矩阵为止。

计算A[1:n]的最优次序包含计算A[1:k]和A[k+1:n]的最优次序，也就是说，得到A[1:k]和A[k+1:n]的最优次序后，二者相乘即得到A[1:n]的最优次序（反证法：因为如果A[1:k]或A[k+1:n]中存在“更优”次序，则A[1:n]的次序也将“更优”，这就与原来A[1:n]的最优次序相矛盾）。

（2）建立递归关系：

设A[i:j],1<=i<=j<=n,所需的最少数乘次数为m[i][j]，则原问题的最优值即为m[1][n]。

当i=j时，无需计算，则m[i][i]=0；

当i<j时，可利用（1）中分析的最优子结构性质来计算m[i][j]，若计算A[i:j]的最优次序在Ak和A(k+1)处断开,i<=k<j则m[i][j] = m[i][k]+m[k+1][j]+p(i-1)*pk*pj；（A[i:k]为p(i-1)*pk矩阵，A[k+1:j]为pk*pj矩阵）

因为k的值在计算之初并不知道具体位置，因此要在j-i个可能中遍历，找到最小的m[i][j]即可。

（3）计算最优值和最优解：

据具体例子：矩阵连乘积A1A2A3A4A5A6，其中各个矩阵的维数为：A1:30*35 A2:35*15 A3:15*5A4:5*10 A5:10×20A6:20*25

源代码如下：

void MatrixChain( int *p, int n, int (*m)[6], int (*s)[6] )
{
	int i, r, j, k, t;
	for( i=1; i<=n; i++ ) { m[i-1][i-1]=0; s[i-1][i-1]=0; }//i=j时，无需计算
	for( r=2; r<=n; r++ )//r为m[i][j]中矩阵个数
		for( i=1; i<=n-r+1; i++ )
		{
			j = i + r - 1;
			m[i-1][j-1] = m[i][j-1] + p[i-1] * p[i] * p[j];	//自底向上计算m[i][j]
			s[i-1][j-1] = i;
			for( k=i+1; k<j; k++ )//通过比较出m[i][j]的最小值，得出最优计算次序和断开位置s[i][j]
			{
				t = m[i-1][k-1] + m[k][j-1] + p[i-1] * p[k] * p[j];
				if( t < m[i-1][j-1] ) { m[i-1][j-1] = t; s[i-1][j-1] = k; }
			}
		}
}

*p:数组p[7]：存储了每个矩阵的维数；

n:单矩阵的个数

*m[6]:数组m[6][6]：存储了每种次序的数乘值；

*s[6]:数组s[6][6]：存储了最优断开位置；

计算次序：

构造最优解：从s[1][n]可知计算A[1:n]的最优次序为：A[1:s[1][n]]*A[s[1][n]+1:n]。而A[1:s[1][n]]的最优次序为：A[1:s[1][s[1][n]]]*A[s[1][s[1][n]]+1:s[1][n]]...照此递归下去，最终可确定最优解结构。

下面是构造最优解的源代码：

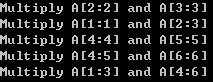
void Traceback( int i, int j, int (*s)[6] )
{
	if( i == j ) return;
	Traceback( i, s[i-1][j-1], s );
	Traceback( s[i-1][j-1]+1, j, s );
	printf( "Multiply A[%d:%d] and A[%d:%d]\n", i, s[i-1][j-1], s[i-1][j-1]+1, j );
}

运行结果：

通过 对上面矩阵连乘问题的分析，我们可以发现动态规划算法的几个基本要素：

（1）具有最优子结构；

（2）具有子问题重叠性质；

因此，我们也可以通过记忆式递归的方法，利用递归来高效地解决矩阵连乘问题。

#include<stdio.h>
int p[7] = { 30, 35, 15, 5, 10, 20, 25 };

int LookupChain( int i, int j, int (*m)[6], int (*s)[6] )
{
	int t, k, u;
	if( m[i -1][j -1] > 0 ) return m[i -1][j -1];//若大于0，则说明m[i-1][j-1]已经计算过了，无需再次递归重复计算，这就是记忆式递归
	if( i == j ) return 0;
	u = LookupChain( i, i, m, s ) + LookupChain( i+1, j, m, s ) + p[i-1] * p[i] * p[j];
	s[i -1][j -1] = i;
	for( k=i+1; k<j; k++ )
	{
		t = LookupChain( i, k, m, s ) + LookupChain( k+1, j, m, s ) + p[i-1] * p[k] * p[j];
		if( t < u )
		{
			u = t;
			s[i -1][j -1] = k;
		}
	}
	m[i -1][j -1] = u;
	return u;
}

int MemorizedMatrixChain( int n, int (*m)[6], int (*s)[6] )
{
	int i, j;
	for( i=1; i<=n; i++ )
		for( j=1; j<=n; j++ ) m[i -1][j -1] = 0;
	return LookupChain( 1, n, m, s );
}



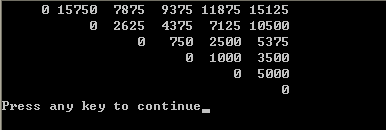
int main()
{
	int i, j, k, n=6;
	int m[6][6], s[6][6]={{0,0}};
	
	MemorizedMatrixChain( n, m, s );

	for( i=1; i<=n; i++ )
	{
		for( k=1; k<=i-1; k++ ) printf("      ");
		k = 1;
		for( j=i; j<=n; j++ )
		{
			if( j == n ) printf("%6d\n",m[i -1][j -1]);
			else printf("%6d",m[i -1][j -1]);
		}
	}
	return 0;
}

运行结果为：

以上为本人对矩阵连乘问题的一点见解，如果谬误，还望见谅啊！