9.1翻译对齐 558
9.1.1分层运动估计 562
9.1.2基于傅立叶的对齐 563
9.1.3逐步完善 566
9.2参数运动 570
9.2.1应用:视频稳定 573
9.2.2基于样条线的运动 575
9.2.3应用:医学图像配准 577
9.3光流 578
9.3.1深度学习方法 584
9.3.2应用:卷帘窗防晃动 587
9.3.3多帧运动估计 587
9.3.4应用:视频降噪 589
9.4分层运动 589
9.4.1应用:帧插值 593
9.4.2透明层和反射 594
9.4.3视频对象分割 597
9.4.4视频对象跟踪 598
9.5额外阅读 600
9.6练习 602

图9.1运动估计:(a-b)基于正则化的光流(Nagel和Enkel- mann1986)©1986 IEEE;(c-d)分层运动估计(Wang和Adelson1994)©1994 IEEE;(e-f)来自评估数据库的样本图像和真实流(Butler、Wulff等人2012)©2012 Springer。
用于对视频序列中的图像进行对齐和估计运动的算法是计算机视觉中最广泛使用的算法之一。例如,帧率图像对齐被广泛用于数字摄像机中以实现其图像稳定(IS)功能。
早期广泛使用的图像配准算法的一个例子是卢卡斯和卡纳德(1981)开发的基于块的平移对齐(光流)技术。该算法的变体几乎被所有运动补偿视频压缩方案所采用,如MPEG/H.263(勒加尔1991)和HEVC/H.265(苏利文、奥姆等人2012)。类似的参数化运动估计算法也被广泛应用于视频摘要(特多西奥和本德1993;伊拉尼和阿南丹1998)、视频稳定(汉森、阿南丹等人1994;斯里尼瓦桑、切拉帕等人2005;松下、奥费克等人2006)以及视频压缩(伊拉尼、许和阿南丹1995;李、陈等人1997)。更复杂的图像配准算法也已开发用于医学成像和遥感。布朗(1992)、齐托娃和弗卢瑟(2003)、戈斯塔斯比(2005)和泽利斯基(2006a)对图像配准技术进行了综述。
为了估计两幅或多幅图像之间的运动,首先需要选择一个合适的误差度量来比较这些图像(第9.1节)。确定了这一点后,必须设计一种合适搜索技术。最简单的方法是穷尽所有可能的对齐方式,即进行全面搜索。实际上,这可能会太慢,因此通常使用基于图像金字塔的层次化粗到精技术(第9.1.1节)。或者,可以使用傅里叶变换(第9.1.2节)来加速计算。
为了在对齐中获得亚像素精度,通常使用基于图像函数泰勒级数展开的增量方法(第9.1.3节)。这些方法也可以应用于参数化运动模型(第9.2节),这些模型用于建模全局图像变换,如旋转或剪切。通过学习被跟踪场景或物体的典型动态或运动统计特性,例如行走人的自然步态(第9.2节),可以提高运动估计的可靠性。对于更复杂的运动,可以使用分段参数样条运动模型(Section9.2.2)。
在存在多个独立(且可能非刚性)运动的情况下,需要使用通用光流(或光学流)技术,如第9.3节所述。近年来,性能最佳的技术开始采用深度神经网络(第9.3.1节)。对于包含大量遮挡的更复杂运动,分层运动模型(第9.4节)可以很好地工作,该模型将场景分解为连贯移动的层次。这些表示还可以用于视频对象分割(第9.4.3节)和对象跟踪(第9.4.4节)。
在本章中,我们将更详细地描述这些技术。更多细节可以在运动估计的综述和比较评估论文中找到(Barron,
Fleet和Beauchemin1994;Mitiche和Bouthemy1996;Stiller和Konrad1999;Szeliski
2006a;Baker,Scharstein等人,2011;Sun,Yang等人,2018;Janai,G等人,2020;Hur
和Roth2020)。
建立两幅图像或图像块之间的一致性的最简单方法是将一幅图像相对于另一幅进行平移。给定一个模板图像I0 (x),在离散像素位置{x=(xi,yi)}处采样,我们希望找到它在图像I1 (x)中的位置。解决这个问题的最小二乘法是找到平方差(SSD)函数的最小值。
其中u =(u,v)表示位移,ei = I1(xi + u)- I0(xi)称为残差误差(或视频编码文献中的位移帧差异)。1(我们暂时忽略I0的某些部分可能位于I1边界之外或不可见的情况。)假设两幅图像中对应的像素值保持不变,通常称为亮度恒定约束。2
一般来说,位移u可以是分数形式,因此需要应用合适的插值函数来处理图像I1 (x)。实际上,双线性插值经常被使用,但双三次插值可以产生略好的结果(Szeliski和Scharstein2004)。彩色图像可以通过累加所有三个颜色通道的差异来进行处理,尽管也可以首先将图像转换到不同的颜色空间,或者仅使用亮度(这在视频编码器中经常这样做)。
稳健的误差度量。我们可以通过用稳健函数P(ei)(Huber1981;Hampel,Ronchetti等1986;Black和Anandan1996;Stewart1999)替换平方误差项,使上述误差度量对异常值更加稳健,以获得
强规范P(e)是一个增长速度慢于二次惩罚的函数
用最小二乘法求解。其中一种函数,有时用于视频运动估计
1使用最小二乘法的通常理由是,它是高斯噪声下的最佳估计。请参见下面关于稳健误差度量的讨论以及附录B.3。
2亮度恒定(Horn1974)是指物体在不同光照条件下保持其感知亮度的趋势。
由于其速度,编码是绝对差值(SAD)度量3或L1范数的总和,即:
然而,由于该函数在原点处不可导,因此不适合使用第9.1.3节中介绍的梯度下降方法。
相反,通常使用一个平滑变化的函数,该函数在小值时是二次的,但在远离原点时增长得更慢。Black和Rangarajan(1996)讨论了各种这样的函数,包括Geman-McClure函数,
(9.4)
其中a是一个常数,可以视为异常值阈值。合适的阈值可以通过稳健统计方法(Huber1981;Hampel,Ronchetti等1986;Rousseeuw和Leroy 1987)得出,例如通过计算中位绝对偏差MAD=medij,并乘以1.4来获得内点噪声过程的标准差的稳健估计(Stewart1999)。Barron(2019)提出了一种广义稳健损失函数,能够建模各种异常分布和阈值,具体讨论见第4.1.3节和附录B.3,该方法还包含一种贝叶斯方法来估计损失函数参数。
空间变化的权重。上述误差指标忽略了这样一个事实:对于给定的对齐,某些被比较的像素可能位于原始图像边界之外。此外,我们可能希望部分或完全降低某些像素的贡献。例如,在拼接马赛克时,当不需要的前景物体已被裁剪掉时,我们可能希望有选择地“删除”图像中的一些部分。对于背景稳定等应用,我们可能希望降低中间部分的权重。
图像的一部分,通常包含被摄像机跟踪的独立移动物体。
所有这些任务都可以通过将空间变化的每个像素权重与两个匹配的图像关联起来来完成。误差度量就变成了加权(或窗口)SSD函数,3在视频压缩中,例如H.264标准(https://www.itu.int/rec/T-REC-H.264),通常使用绝对变换差之和(SATD),其测量频率变换空间中的差异,例如使用哈达玛变换,因为其更准确地预测质量(Richardson2003)。
如果允许大量的潜在运动,则上述度量可能会偏向于较小的重叠解决方案。为了抵消这种偏差,可以将窗口SSD分数除以重叠面积
(9.6)
计算每个像素(或平均)的像素误差EWSSD /A。该量的平方根是均方根强度误差
RMS =√
(9.7)
经常在比较研究中报告。
偏移和增益(曝光差异)。通常,被对齐的两幅图像并非以相同的曝光度拍摄。两个图像之间线性(仿射)强度变化的简单模型是偏移和增益模型,
I1 (x + u) = (1 + Q)I0 (x) + β, (9.8)
其中,β是偏置,Q是增益(Lucas和Kanade 1981;Gennert 1988;Fuh和Maragos1991;Baker、Gross和Matthews 2003;Evangelidis和Psarakis 2008)。最小二乘法公式如下
与其简单地计算对应区域之间的平方差,有必要进行线性回归(附录A.2),这会稍微增加成本。请注意,对于彩色图像,可能需要为每个颜色通道估计不同的偏置和增益,以补偿某些数码相机自动执行的颜色校正(第2.3.2节)。偏置和增益补偿在视频编解码器中也有应用,称为加权预测(Richardson2003)。
一种更通用(空间变化、非参数)的强度变化模型,在配准过程中作为计算的一部分,被Negahdaripour(1998)、Jia和Tang(2003)以及Seitz和Baker(2009)使用。这有助于处理局部变化,例如广角镜头、大光圈或镜头外壳引起的暗角。此外,还可以在比较图像值之前对其进行预处理,例如使用带通滤波图像(Anandan 1989;Bergen,Anandan等1992),或梯度(Scharstein 1994;Papenberg,Bruhn等2006),或其他局部变换,如直方图或秩。
变换(Cox、Roy和Hingorani 1995;Zabih和Woodfill 1994),或最大化互信息(Viola和Wells III 1997;Kim、Kolmogorov和Zabih 2003)。Hirschm ller和Scharstein(2009)比较了这些方法中的几种,并报告了它们在曝光差异场景中的相对性能。
相关性。除了计算强度差之外,还可以进行相关性分析,即最大化两个对齐图像的乘积(或互相关),
(9.10)
乍一看,这似乎使得偏差和增益建模变得不必要,因为图像将倾向于对齐,而不管它们的相对尺度和偏移。然而,实际上
不正确。如果I1 (x)中存在一个非常亮的区域,那么最大乘积可能实际上位于该区域内。
在哪里
(9.13)
是相应补丁的平均图像,N是补丁中的像素数。归一化互相关得分始终保证在[-1,1]范围内,这使得在某些高级应用中更容易处理,例如判断哪些补丁真正匹配。当匹配不同曝光度拍摄的图像时,归一化相关性表现良好,例如在创建高动态范围图像时(第10.2节)。然而,需要注意的是,如果两个补丁中的任何一个方差为零,则NCC得分是未定义的(实际上,其性能在噪声低对比度区域会下降)。
NCC的变体与匹配分数(9.9)中隐含的偏置-增益回归有关,即归一化SSD分数
由Criminisi、Shotton等人(2007)提出。在他们的实验中,他们发现它产生的结果与NCC相当,但当使用移动平均技术应用于大量重叠的补丁时,它更有效率(第3.2.2节)。
既然我们有了一个明确的对齐成本函数需要优化,如何找到其最小值呢?最简单的办法是在某个范围内的平移上进行全面搜索,使用整数或亚像素步长。这通常是用于运动补偿视频压缩中块匹配的方法,其中探索了一系列可能的运动(例如,±16像素)。4
为了加快这一搜索过程,通常采用层次运动估计:构建图像金字塔(第3.5节),首先在较粗的层级上对较少数量的离散像素(对应相同的运动范围)进行搜索(Quam1984;Anandan1989;Bergen,Anandan等1992)。然后利用金字塔某一层的运动估计来初始化下一层更精细的局部搜索。或者,可以从粗层中使用多个种子(好的解决方案)来初始化细层搜索。虽然这不能保证产生与完整搜索相同的结果,但通常效果几乎一样好,而且速度快得多。
更正式地说,设
Ik (l)(xj) ← k (l-1)(
2xj ) (9.15)
是通过子采样(下采样)在第l级的平滑图像版本得到的被削减的图像。有关如何执行所需的下采样(金字塔构造),而不引入过多混叠,请参见第3.5节。
在最粗略的层面上,我们寻找最佳位移u(l),以最小化图像I0(l)和I1(l)之间的差异。这通常通过在位移u(l)的某个范围内进行全面搜索来完成,范围为∈2-l[-S;S]²,其中S是最精细(原始)分辨率水平下的期望搜索范围,之后可选择进行第9.1.3节中描述的增量细化步骤。
一旦估计出合适的运动矢量,就用它来预测可能的位移
(l-1) ← 2u(l)
(9.16)
4在立体匹配(第12.1.2节)中,由于潜在位移的1D特性,搜索假设的数量要小得多,因此几乎总是对所有可能的视差进行显式搜索(即平面扫描)。
对于下一个更精细的层次。5在更精细的层次上,位移搜索会在一个更窄的位移范围内重复进行,例如(l—1)士1,再次可选择与增量细化步骤结合(Anandan 1989)。或者,可以使用当前运动估计对图像进行变形(重采样),在这种情况下,只需在更精细的层次上计算小幅度的增量运动。Bergen、Anandan等人(1992)提供了整个过程的详细描述,扩展到了参数化运动估计(第9.2节)。
当搜索范围对应于较大图像的显著部分(如图像拼接的情况,见第8.2节),层次方法可能效果不佳,因为通常无法在重要特征被模糊之前过度细化表示。在这种情况下,基于傅里叶的方法可能更为合适。
基于傅里叶的对齐依赖于移位信号的傅里叶变换这一事实
与原始信号具有相同的幅度,但相位线性变化(第3.4节),即F {I1(x + u)} = F {I1 (x)} e—ju·!=I1(!)e—ju·!, (9.17)
其中,!是傅里叶变换的向量值角频率,我们使用符号I1(!)= F {I1 (x)}来表示信号的傅里叶变换(第3.4节)。
傅里叶变换的另一个有用特性是,空间域中的卷积对应于傅里叶域中的乘法(第3.4节)。因此,交叉相关函数ECC的傅里叶变换可以写为
在哪里
(9.19)
是相关函数,即一个信号与另一个信号的反向的卷积,而I(!)是I1(!)的复共轭。这是因为卷积被定义为
一个信号与另一个信号的反向相加(第3.4节)。
5这种位移加倍仅在位移以整数像素坐标定义时才必要,这是文献中常见的做法(Bergen,Anandan等,1992)。如果使用归一化的设备坐标(Section2.1.4),则各层级的位移(和搜索范围)无需改变,尽管步长需要调整,以保持搜索步长大致不超过一个像素。
事实上,傅里叶移位性质(9.17)是从卷积定理中得出的,因为观察到移位等同于与一个位移的delta函数δ(x - u)进行卷积。
为了高效地评估ECC在所有可能的u值范围内,我们对图像I0 (x)和I1 (x)分别进行傅里叶变换,将两个变换相乘(在将第二个变换取共轭后),然后取结果的逆变换。快速傅里叶变换算法可以在O(NM log NM)次操作中计算出一个N×M图像的变换(Bracewell1986)。这比考虑图像重叠范围全貌所需的O(N^2 M^2)次操作要快得多。
虽然基于傅里叶的卷积常用于加速图像相关性的计算,但它也可以用于加速平方差函数(及其变体)的计算。考虑公式(9.1)给出的平方差公式。其傅里叶变换可以表示为
(9
.20)
因此,SSD函数可以通过取相关函数的两倍并从两个图像(或补丁)的能量之和中减去它来计算。
窗口相关。遗憾的是,傅里叶卷积定理仅适用于在两个图像的所有像素上进行求和的情况,当访问超出原始边界外的像素时,需要使用图像的循环移位。虽然对于小偏移和大小相当的图像来说这是可以接受的,但当图像重叠很小或一个图像是另一个的小子集时,这种方法就毫无意义了。
在这种情况下,交叉相关函数应被窗口(加权)交叉相关函数所取代,
(9.22)
其中加权函数w0和w1在图像的有效范围之外为零,并且两个图像都被填充,使得循环移位返回原始图像边界之外的0值。
一个更有趣的例子是计算方程(9.5)中引入的加权SSD函数,
将此展开为相关性的总和并推导出适当的傅里叶变换集,留待练习9.1。
同样的推导方法也可以应用于偏差-增益校正后的平方差函数EBG(9.9)。同样地,可以使用傅里叶变换高效计算所有相关性,以进行偏差和增益参数的线性回归,从而估计每个潜在位移下的曝光补偿差异(练习9.1)。此外,还可以利用傅里叶变换来估计两个中心位于同一像素上的区域之间的旋转和尺度,如De Castro和Morandi(1987)以及Szeliski (2010,第8.1.2节)所述。
相位相关。一种用于运动估计的常规相关(9.18)的变体是相位相关(Kuglin和Hines 1975;Brown 1992)。在这里,两个待匹配信号的谱通过将(9.18)中每个频率乘积除以傅里叶变换的幅度来白化,
(9.24)
在进行最终逆傅里叶变换之前。对于具有完美(循环)移位的无噪声信号,我们有I1(x + u)= I0 (x),因此,根据公式(9.17),我们得到
F{I1(x+u)}=I1(!)e—2πju·! = I0(!)和
F {EPC (u)} = e —2πju·! . (9.25)
因此,相位相关(在理想条件下)的输出是一个位于u的正确值处的单个尖峰(脉冲),这(原则上)使得更容易找到正确的估计。
相位相关在某些领域被认为优于常规相关,但这种表现取决于信号和噪声的特性。如果原始图像受到窄频带噪声(例如低频噪声或峰值频率“嗡嗡”声)的影响,白化过程实际上会减弱这些区域的噪声。然而,如果原始信号在某些频率上的信噪比非常低(比如两张模糊或纹理粗糙且高频噪声较多的图像),白化过程反而可能降低性能(见练习9.1)。
梯度交叉相关已成为相位相关的一种有前途的替代方法(Argyriou和Vlachos,2003),尽管可能需要进一步的系统研究。Fleet和Jepson(1990)也研究了相位相关作为估计的方法。

图9.2函数的泰勒级数近似和光流校正量增量计算。J1(xi + u)是(xi + u)处的图像梯度,ei是当前强度差。
9.1.3逐步完善
到目前为止所描述的技术可以估计与最近像素的对齐(如果使用更小的搜索步骤,则可以估计与潜在的分数像素的对齐)。一般来说,图像稳定和拼接应用需要更高的精度才能获得可接受的结果。
为了获得更好的亚像素估计,我们可以采用天和胡恩斯(1986)描述的几种技术之一。一种方法是在找到的最佳值周围评估几个离散(整数或分数)的(u,v)值,并通过插值匹配得分来找到解析最小值(Szeliski和Scharstein 2004)。
更常用的方法是,首先由Lucas和Kanade(1981)提出,在SSD能量函数(9.1)上进行梯度下降,使用图像函数的泰勒级数展开(图9.2),
(9.27)
(9.28)
在哪里
ei = I1(xi + u)- I0(xi), (9.30)
在(9.1)中首次介绍的是电流强度误差。7在特定子像素处的梯度
位置(xi + u)可以使用多种技术计算,其中最简单的是
7我们遵循机器人学中常用的惯例,以及Baker和Matthews(2004)的惯例,即关于(列)向量的导数结果为行向量,因此公式中需要的转置更少。
仅仅是为了获取像素x和x +(1,0)或x +(0,1)之间的水平和垂直差异。更复杂的导数有时会导致明显的性能改进。
SSD误差(9.28)增量更新的线性化形式通常被称为
光流约束或亮度恒定约束方程(Horn和Schunck1981)Ixu + Iy v + It = 0, (9.31)
其中Ix和Iy中的下标表示空间导数,而It称为时间导数,如果我们在计算视频序列中的瞬时速度,这是有意义的。当平方并求和或在区域上积分时,它可以用来计算光流(Horn和Schunck1981)。
上述最小二乘问题(9.28)可通过求解相关正规方程(附录A.2)来最小化,
A△u = b (9.32)
(9.33)
分别称为(高斯-牛顿近似)Hessian矩阵和梯度加权残差向量。8这些矩阵也常写为
以
及
(9.35)
所需用于J1(xi + u)的梯度可以在估计I1(xi + u)所需的图像变形同时计算(第3.6.1节(3.75)),实际上,这些梯度通常作为图像插值的副产品被计算。如果效率是关注点,可以使用模板图像中的梯度来替代这些梯度,
J1(xi + u)≈J0(xi), (9.36)
因为接近正确的对齐,模板和位移目标图像应该看起来相似。这具有允许预计算Hessian和Jacobi矩阵的优点
图像处理可以显著节省计算资源(Hager和Belhumeur 1998;Baker和Matthews 2004)。通过将用于计算(9.30)中ei的变形图像I1(xi + u)表达为子像素插值滤波器与I1中离散样本的卷积,可以进一步减少计算量(Peleg和Rav-Acha 2006)。预先计算梯度场与I1移位版本之间的内积,使得ei的迭代重新计算可以在常数时间内完成(与像素数量无关)。
上述增量更新规则的有效性取决于泰勒级数近似的质量。当远离真实位移(例如,1-2像素)时,可能需要多次迭代。然而,可以通过最小二乘法拟合一系列较大的位移来估计J1的值,以扩大收敛范围(Jurie和Dhome2002),或者为给定的补丁“学习”一个专用识别器(Avidan2001;Williams、Blake和Cipolla2003;Lepetit、Pilet和Fua2006;Hinterstoisser、Benhimane
(如Section7.1.5中所讨论的,et al.2008;zuysal,Calonder et al.2010)。
常用的增量更新停止标准是监测位移校正ⅡuⅡ的大小,当其降至某个阈值以下(例如,1/10像素)时停止。对于较大的运动,通常会将增量更新规则与分层的粗到精搜索策略结合使用,具体如第9.1.1节所述。
条件性和孔径问题。有时,由于待对齐区域缺乏二维纹理,线性系统(9.32)的逆运算可能会变得条件不良。一个常见的例子是孔径问题,最早在一些早期关于光流的研究论文中被识别(Horn和Schunck 1981),后来由Anandan进行了更深入的研究(1989)。考虑一个图像块,其中包含一条向右移动的斜边(图7.4)。在这种情况下,只有速度(位移)的法向分量可以可靠地恢复。这在(9.32)中表现为秩亏矩阵A,即其较小的特征值非常接近零。
当方程(9.32)求解时,沿边缘的位移分量条件非常差,在小噪声扰动下可能导致离谱的猜测。一种缓解此问题的方法是在预期运动范围内添加先验(软约束)(Simoncelli,Adelson,和Heeger1991;Baker,Gross,和Matthews2004;Govindu2006)。这可以通过向A的对角线添加一个小值来实现,这实际上使解偏向于较小的△u值,但仍(大部分)最小化平方误差。 然而,当使用简单的(固定的)二次先验时,如Simoncelli、Adelson和Heeger(1991)所假设的纯高斯模型,在实践中并不总是成立,例如,因为
即沿强边界的混叠(Triggs2004)。因此,在进行矩阵求逆之前,可以谨慎地将较大特征值的一小部分(例如5%)添加到较小的特征值中。
不确定性建模。特定基于补丁的运动估计的可靠性可以通过不确定性模型更正式地捕捉。最简单的模型是协方差矩阵,它捕捉了运动估计在所有可能方向上的预期方差。如第8.1.4节和附录B.6所述,在少量加性高斯噪声下,可以证明协方差矩阵Σu与海森矩阵A的逆成正比,
Σu = σA —1 , (9.37)
其中σ是加性高斯噪声的方差(Anandan1989;Matthies,Kanade,
和Szeliski1989;Szeliski1989)。
对于较大的噪声量,卢卡斯-坎纳德算法在(9.28)中进行的线性化只是近似的,因此上述量成为真实协方差的克拉美罗下界。因此,海森矩阵A的最小和最大特征值现在可以解释为运动最不确定和最确定方向上的(缩放后的)逆方差。(Steele和Jaynes(2005)给出了使用更现实的图像噪声模型的更详细分析。)图7.5显示了图像中三个不同像素位置的局部SSD表面。如你所见,表面在高纹理区域有一个明显的最小值,并且在强边缘附近受到光圈问题的影响。
偏差和增益、加权和鲁棒误差度量。Lucas-Kanade更新规则也可应用于偏差-增益方程(9.9)
(Lucas和Kanade1981;Gennert1988;Fuh和Maragos1991;Baker、Gross和Matthews 2003)。由此得到的4×4方程组可以同时求解,以估计平移位移更新△u和偏置和增益参数β和Q。
对于具有线性外观变化的图像(模板),可以推导出类似的公式,
λj Bj
9.39)
其中Bj (x)是基图像,λj是未知系数(Hager和Belhumeur1998;Baker、Gross等人2003;Baker、Gross和Matthews2003)。潜在
线外观变化包括光照变化(Hager和Belhumeur1998)和
小非刚性变形(Black和Jepson1998;Kambhamettu、Goldgof等人2003)。也可以使用加权(窗口)版本的Lucas-Kanade算法:请注意,在从原始加权SSD函数(9.5)推导Lucas-Kanade更新时,我们忽略了对w1(xi + u)加权函数关于u的导数,这在实践中通常是可接受的,特别是当加权函数是一个具有相对较少过渡的二进制掩模时。
贝克、格罗斯等人(2003)仅使用了w0 (x)项,如果两幅图像具有相同的范围且重叠区域没有(独立的)遮挡,则这一方法是合理的。他们还讨论了将权重与▽I(x)成比例的想法,这有助于处理非常嘈杂的图像,其中梯度本身也是噪声。类似的观点,以总最小二乘法的形式表述(范胡菲尔和范德瓦尔1991;范胡菲尔和莱默林2002),也被其他研究光流的研究者提出(韦伯和马利克1995;巴巴-哈迪亚沙尔和
Suter1998b;M hlich和Mester1998)。Baker、Gross等人(2003)展示了如何进行评估
对于足够大的图像,即使只使用了5-10%的像素,方程(9.40)在最可靠(最高梯度)的像素处也不会显著降低性能。(这一想法最初由Dellaert和Collins(1999)提出,他们使用了更复杂的选取标准。)
Lucas-Kanade增量细化步骤也可以应用于第9.1节中介绍的稳健误差度量,
ELK—SRD
(9.41)
可使用第8.1.4节中描述的迭代加权最小二乘法技术解决。
许多图像对齐任务,例如手持相机拍摄的图像拼接,需要使用更复杂的运动模型,如第2.1.1节所述。这些模型,例如仿射变形,通常比纯平移具有更多的参数,因此在整个可能值范围内进行完整搜索是不切实际的。相反,增量卢卡斯-坎纳德算法可以推广到参数化运动模型,并与层次搜索算法结合使用(Lucas和Kanade 1981;Rehg和Witkin 1991;Fuh和Maragos 1991;
Bergen、Anandan等人1992;Shashua和Toelg1997;Shashua和Wexler2001;Baker和Matthews2004)。
对于参数化运动,我们不再使用单一的常数平移向量u,而是采用空间变化的运动场或对应图x(x;p),该图由低维向量p参数化,其中x可以是第2.1.1节中介绍的任何运动模型。参数化的增量运动更新规则现在变为
即,图像梯度▽I1与对应场的雅可比矩阵Jx,=∂x/∂p的乘积。
表8.1给出了第2.1.1节和表2.1中介绍的二维平面变换的运动雅可比矩阵Jx。请注意,我们重新参数化了这些运动矩阵,使其在原点p = 0时始终为单位矩阵。这在后续讨论组合算法和逆组合算法时会非常有用。(这也使得对运动施加先验条件变得更加容易。)
对于参数化运动,(高斯-牛顿)Hessian和梯度加权残差向量变为
(9.46)
(9.47)
注意方括号内的表达式与简单平移运动情况(9.33–9.34)中计算出的相同。
基于块的近似。参数化运动的海森矩阵和残差向量的计算可能比平移情况下的计算成本高得多。对于具有n个参数和N个像素的参数化运动,A和b的累积需要O(n^2 N)次操作(Baker和Matthews 2004)。一种显著减少这种计算量的方法是
该方法是将图像划分为更小的子块(补丁)Pj,并且仅在像素级别上累积方括号内的简单2×2量(Shum和Szeliski,2000),
(9.48)
ei ▽I
(9.49)
然后可以近似地得到完整的Hessian和残差
和
其中,j是每个补丁Pj的中心(Shum和Szeliski2000)。这相当于用分段常数近似代替真实运动雅可比矩阵。实际上,这种方法效果很好。
组合方法。对于像单应性这样的复杂参数运动,计算运动雅可比矩阵变得复杂,并可能涉及逐像素除法。Szeliski和Shum(1997)观察到,这可以通过首先根据当前运动估计xI(x;p)对目标图像I1进行变形来简化,
1 (x)
= I1 (xI (x; p)), (9.52)
然后将这个扭曲的图像与模板I0 (x)进行比较。随后,Hager和Belhumeur(1998)建议用I0 (x)的梯度替换I1 (x)的梯度,如前所述的(9.36),这使得可以预计算(并求逆)给定在(9.46)中的海森矩阵A。残差向量b(9.47)也可以部分预计算,即最速下降法图像▽I0可以预先计算并存储,以便稍后与e(x) = I1 (x)—I0 (x)误差图像相乘,如(Szeliski 2010,第8.2节)和(Baker和Matthews 200
)所述,这种方法称为逆加法方案。Baker和Matthews(2004)还介绍了一种变体,他们称之为逆组合算法,在该算法中,他们对模板图像I0 (x)进行扭曲,并预计算逆海森矩阵和最速下降法图像,使其成为首选方法。他们还讨论了使用高斯-牛顿迭代的优势(即一阶展开)。
与最速下降法和Levenberg-Marquardt等其他方法相比,最小二乘法(如上所述)具有优势。
后续系列文章(Baker,Gross等,2003;Baker,Gross和Matthews,2003,2004)讨论了更高级的主题,如逐像素加权、效率优化的像素选择、稳健度量和算法的深入探讨、线性外观变化以及参数先验。这些内容对于任何希望实现高度调优的增量图像配准的人来说都是极其宝贵的读物,并且已被广泛用作后续目标跟踪器的组件,相关内容将在第9.4.4节中讨论。Evan Evangelidis和Psarakis(2008)提供了这些及其他相关方法的一些详细实验评估。
学习运动模型
参数化运动场的一种替代方法是学习一组针对特定应用定制的基础函数(Black,Yacoob等,1997)。首先,从一组训练视频中计算出一组密集的运动场(第9.3节)。接着,对运动场堆栈ut (x)应用奇异值分解(SVD),以计算前几个奇异向量vk (x)。最后,对于新的测试序列,使用粗到精算法估计参数化流场中的未知系数ak,从而计算出新的流场。
u (x) = akvk (x). (9.53)
图9.3a展示了通过观察行走视频学习到的一组基场。图9.3b显示了基系数的时间演变以及几个恢复的参数化运动场。请注意,类似的思想也可以应用于特征轨迹(Torresani、Hertzmann和Bregler 2008),这一主题我们将在第7.1.5节和第13.6.4节中详细讨论,同时还有视频稳定技术(Yu和Ramamoorthi 2020)。
视频稳定是参数运动估计最广泛的应用之一(Hansen,Anandan等,1994;Irani,Rousso和Peleg,1997;Morimoto和Chellappa,1997;Srinivasan,Chellappa等,2005;Grundmann,Kwatra和Essa,2011)。用于稳定性的算法既可以在硬件设备中运行,如摄像机和静态相机,也可以在软件包中运行,以提高抖动视频的视觉质量。

图9.3学习的参数化运动场对于一个行走序列(Black,Yacoob等人
(Al.1997)©1997 IEEE:(a)学习基流场;(b)随时间变化的运动系数图和相应的估计运动场。
在关于全帧视频稳定性的论文中,松下、奥费克等人(2006)对稳定性的三个主要阶段进行了很好的概述,即运动估计、运动平滑和图像变形。运动估计算法通常使用相似变换来处理相机的平移、旋转和变焦。难点在于让这些算法锁定背景运动,这是由相机移动引起的,而不被独立移动的前景物体所干扰(余和拉马莫尔蒂2018,2020;余、拉马莫尔蒂等2021)。运动平滑算法恢复运动的低频部分(缓慢变化的部分),然后估计需要消除的高频抖动成分。虽然常用的运动导数二次惩罚,但通过导数的L1最小化可以实现更真实的虚拟相机运动(锁定且线性)(格伦德曼、夸特拉和埃萨2011)。最后,图像变形算法应用高频校正,使原始帧看起来像是相机仅经历了平滑运动。
生成的稳定算法可以显著改善抖动视频的外观,但它们通常仍包含视觉伪影。例如,图像扭曲可能导致图像边缘缺失,这些边缘需要裁剪、使用其他帧的信息填充或通过修复技术(第10.5.1节)来补全。此外,在快速运动中捕捉到的视频帧往往模糊不清。可以通过使用去模糊技术(第10.3节)或从运动较少或对焦更好的其他帧中借用更清晰的像素来改善其外观(松下、奥费克等人,2006年)。练习9.3要求你实现并测试这些想法。
在摄像机大量翻译3D的情况下,例如,当摄像师在
步行时,更好的方法是从相机运动和三维场景的运动重建中计算出完整的结构。然后可以计算一条或多条平滑的三维相机路径,并使用插值后的三维点云作为代理几何,通过视图插值重新渲染原始视频,同时保留显著特征,这有时被称为内容保持变形(Liu,Gleicher等2009,2011;Liu,Yuan等2013;Kopf,Cohen和Szeliski 2014)。如果你有多个摄像头阵列而不是单个摄像机,可以采用光场渲染方法(第14.3节)(Smith,Zhang等2009)来实现更佳效果。
虽然参数化运动模型在各种应用中都很有用(如视频稳定和映射到平面表面上),但大多数图像运动太复杂,无法被这样的低维模型捕捉。
传统上,光流算法(第9.3节)为每个像素计算一个独立的运动估计值,即计算出的流向量数等于输入像素数。因此,一般光流方程(9.1)可以写成
经
济、社会和文化事务部 (9.54)
注意,在上面的方程式中,变量的数量{ui }是测量数量的两倍,所以问题是没有约束的。
我们将在第9.3节中研究的两种经典方法是,在重叠区域(基于补丁或窗口的方法)上进行求和,或者使用正则化或马尔可夫随机场(第四章)在{ui }场中添加平滑项。在本节中,我们将介绍一种介于一般光流(每个像素独立的运动)和参数化流(少量全局参数)之间的替代方法。该方法是将运动场表示为二维样条函数。
j Bj
j wi;
j , (9.55)
其中,Bj(xi)称为基函数,仅在有限的支撑区间内非零(Szeliski和Coughlan1997)。我们称wij = Bj(xi)为权重,以强调{ui }是{j }的已知线性组合。
将单个像素流向量ui(9.55)的公式代入SSD误差度量(9.54),得到一个类似于方程(9.43)的参数运动公式。最大的

图9.4样条运动场:位移向量ui=(ui,vi)以加号(+)表示,由较少的控制顶点j =(i,j)控制,以圆圈(.)表示。
不同之处在于,雅可比矩阵J1(xi9)(9.45)现在由权重矩阵W = [wij ]中的稀疏项组成。
在我们对运动场有更多的了解的情况下,例如当运动是由静态场景中的摄像机移动引起的时,我们可以使用更专业的运动模型。例如,平面加视差模型(第2.1.4节)可以自然地与基于样条的运动表示相结合,其中平面内的运动由同态(8.19)表示,而平面外的视差d则由每个样条控制点上的标量变量表示(Szeliski和Kang 1995;Szeliski和Coughlan 1997)。
在许多情况下,少量的样条顶点会导致一个条件良好的运动估计问题。然而,如果在多个样条区域中存在大片无纹理区域(或受孔径问题影响的拉长边缘),可能需要添加正则化项以使问题变得适定(第4.2节)。最简单的方法是直接在样条控制网格{j }中相邻顶点之间添加平方差惩罚项,如公式(4.24)所示。如果采用多分辨率(粗到细)策略,则在逐层转换时重新缩放这些平滑项非常重要。
与基于样条的运动估计器相对应的线性系统是稀疏且规则的。由于其通常规模适中,因此可以使用直接技术如乔列斯基分解(附录A.4)来求解。或者,如果问题变得过大并受到过多填充的影响,则可以使用迭代技术,如层次预条件共轭梯度法(Szeliski1990b,2006b;Krishnan和Szeliski2011;Krishnan、Fattal和Szeliski2013)(附录A.5)。
由于其稳健性,基于样条的运动估计已被用于许多应用,包括视觉效果(Roble1999)和医学图像配准(Sec-

图9.5基于四叉树样条的运动估计(Szeliski和Shum1996)©1996
IEEE:(a)四叉树样条表示,(b)这可能导致裂缝,除非白色节点被限制依赖于其父节点;(c)变形的四叉树样条网格叠加在灰度图像上;(d)流场以针图形式可视化。
第9.2.3条)(Szeliski和Lavall
e1996;Kybic和Unser2003)。
然而,基本技术的一个缺点是,在运动不连续处模型表现不佳,除非使用过多的节点。为了改善这一状况,Szeliski和Shum(1996)提出在样条控制网格中嵌入四叉树表示(图9.5a)。大单元用于呈现平滑运动区域,而小单元则添加在运动不连续的区域(图9.5c)。
为了估计运动,采用了一种从粗到精的策略。首先,在低分辨率图像上施加一个规则样条,获得初始运动估计。对于运动不一致的样条区域,即残差平方(9.54)超过阈值的部分,将其细分为更小的区域。为了避免在最终的运动场中出现裂纹(图9.5b),需要限制某些节点的值,这些节点位于细化网格中,即靠近较大单元的节点,使其依赖于其父节点的值。这最简单的方法是使用四叉树样条的层次基表示(Szeliski 1990b),并选择性地将一些层次基函数设为0,如(Szeliski和Shum 1996)所述。
因为样条基运动模型擅长表示平滑的弹性变形场,在医学图像配准中得到了广泛应用(Bajcsy和Kovacic 1989;Szeliski和Lavalle 1996;Christensen、Joshi和Miller1997).10。配准技术既可用于跟踪个体
患者随时间的发展或进展(alon-
纵向研究)或将不同的患者图像匹配在一起,以发现共同点和去
10在计算机图形学中,这种弹性体积变形被称为自由形式变形(Sederberg和Parry1986;Coquillart1990;Celniker以及Gossard1991)。

图9.6弹性脑配准(Kybic和Unser 2003)©2003 IEEE:(a)原始脑图谱和患者MRI图像以红绿叠加;(b)弹性配准后,使用八个用户指定的标志点(未显示);(c)立方B样条变形场,显示为变形网格。
结构变异或病理(横断面研究)。当不同成像模式进行配准时,例如计算机断层扫描(CT)和磁共振成像(MRI),通常需要相似性互信息测量(Viola和Wells III 1997;Maes,Collignon等1997)。
Kybic和Unser(2003)提供了一篇很好的文献综述,并描述了一个完整的系统,该系统通过将图像和变形场表示为多分辨率样条来实现。图9.6展示了Kybic和Unser系统用于将患者的脑部MRI与标记的脑图谱图像配准的一个例子。该系统可以完全自动运行,但通过定位几个关键标志点可以获得更准确的结果。关于可变形医学图像配准的最新论文,包括性能评估,包括Klein、Staring和Pluim(2007)、Glocker、Komodakis等人(2008)以及Sotiras、Davatzikos和Paragios(2013)的综述。
与其他应用程序一样,常规体积样条可以通过选择性细化来增强。在三维体积图像或表面配准的情况下,这些被称为八叉树样条(Szeliski和Lavall 1996),已用于配准不同患者的医学表面模型,如椎骨和面部图9.7)。
运动估计最普遍(也是最具挑战性)的版本是计算每个像素的独立运动估计,这通常被称为光流(或视流)。

图9.7基于八叉树样条的两个椎体表面模型的图像配准(Szeliski
以及Lavall e1996)©1996 Springer:(a)在初始刚性对齐后;(b)在弹性对齐后;(c)穿过适应的八叉树样条变形场的横截面。
我们在上一节中提到,这通常涉及到最小化图像中对应像素的亮度或颜色差异,
经
济、社会和文化事务部 (9.56)
由于变量数量{ui }是测量次数的两倍,问题变得欠约束。解决这一问题的两种经典方法是:在重叠区域(基于补丁或窗口的方法)上局部求和,或者使用正则化或马尔可夫随机场(第4章)对{ui }场添加平滑项,并寻找全局最小值。关于最近光流算法的良好综述,可参见Baker、Scharstein等人(2011年)、Sun、Yang等人(2018年)、Janai、Gnei等人(2020年)以及Hur和Roth(2020年)。
基于补丁的方法通常涉及使用位移图像函数(9.28)的泰勒级数展开来获得亚像素估计值(Lucas和Kanade 1981)。Anand(1989)展示了如何在粗到细的金字塔方案中,将一系列局部离散搜索步骤与Lucas-Kanade的增量细化步骤交织在一起,这使得可以估计大运动,如第9.1.1节所述。他还分析了局部运动估计的不确定性与局部海森矩阵Ai(9.37)的特征值之间的关系,如图7.4和7.5所示。
伯根、阿南丹等人(1992)开发了一个统一的框架,用于描述参数化(第9.2节)和基于补丁的光流算法,并对这一主题进行了很好的介绍。在粗到精的金字塔中每次迭代光流估计后,他们重新校正其中一张图像,以便仅计算增量光流估计(第9.1.1节)
当使用重叠的补丁时,一种有效的实现方法是首先计算每个像素处梯度和强度误差(9.33–9.34)的外积,然后使用移动平均滤波器执行重叠窗口求和。11
霍恩和舒克(1981)没有独立求解每个运动(或运动更新),而是开发了一个基于正则化的框架,在该框架中,(9.56)在所有流向量{ui }上同时最小化。为了约束问题,增加了平滑性约束,即对流导数的平方惩罚,加入到基本的逐像素误差度量中。由于该技术最初是在变分(连续函数)框架下为小运动开发的,因此与(9.28)相对应的线性化亮度恒定约束,即(9.31),通常被写成一个解析积分。
EHS =∫(Ixu + Iy v + It)2 dx dy, (9.57)
其中(Ix,Iy)=▽I1=J1,It = ei表示时间导数,即图像之间的亮度变化,而u(x,y)和v(x,y)是二维光流函数。Horn和Schunck模型也可以视为基于样条的运动估计的极限情况,当样条变为1×1像素块时。
也可以将局部和全局流量估计的思想结合到一个单一框架中,方法是使用局部聚合(而非单像素)的海森矩阵作为亮度恒定项(Bruhn,Weickert和Schn rr 2005)。考虑离散形式的解析全局能量(9.57),即(9.28),
EHSD = ui + 2eiJui
+ e
(9.58)
如果我们用面积代替每个像素(秩1)的Hessian Ai = [JiJ]和残差bi = Jiei
通过聚合版本(9.33–9.34),我们得到了一个全局最小化算法,其中使用了基于区域的亮度约束。
对基本光流模型的另一种扩展是结合全局(参数化)和局部运动模型。例如,如果我们知道运动是由相机在静态场景中移动引起的(刚体运动),我们可以重新定义问题,即估计每个像素的深度以及全局相机运动的参数(Adiv1989;Hanna 1991;Bergen,Anandan等1992;Szeliski和Coughlan 1997;Nir,Bruckstein和Kim- mel 2008;Wedel,Cremers等2009)。这些技术与立体匹配密切相关(第12章)。或者,我们也可以估计每幅图像或每段的仿射运动模型,并结合每个像素的残差校正(Black和Jepson 1996;Ju,Black和
11在此阶段也可使用其他平滑或聚合过滤器(Bruhn、Weickert和Schn rr 2005)。
Jepson1996;Chang、Tekalp和Sezan1997;M min和P rez2002)。我们
将在第9.4节中重新讨论这个话题。
当然,图像亮度可能并不总是衡量外观一致性的一个合适指标,例如当图像中的光照变化时。如第9.1节所述,匹配梯度、滤波图像或其他指标,如图像赫西安(二阶导数测量)可能更为合适。还可以局部计算图像中可转向滤波器的相位,这不受偏置和增益变换的影响(Fleet和Jepson 1990)。Papenberg、Bruhn等人(2006)回顾并探讨了这些约束条件,并提供了在增量流计算过程中迭代重配图像的详细分析和理由。
由于亮度恒定性约束是在每个像素独立评估的,而不是在可能违反恒定流假设的区域求和,因此全局优化方法在运动不连续处表现更好。特别是当使用鲁棒度量作为平滑性约束时(Black和Anandan 1996;Bab-Hadiashar和Suter1998a).12),L1范数,即总变差(TV)是一种流行的鲁棒度量选择,它产生了一个凸能量函数,可以找到其全局最小值(Bruhn,Weickert,和Schn rr2005;Papenberg,Bruhn等2006;Zach,Pock,和Bischof2007b;Zimmer,Bruhn,和Weickert2011)。各向异性平滑性先验是另一种流行的选择,它在图像梯度平行和垂直方向上应用不同的平滑
性(Nagel和Enkelmann 1986;Sun,Roth等2008;Werlberger,Trobin等2009;Werlberger,Pock,和Bischof2010)。还可以从一组配对的流场和强度图像中学习一组更好的平滑性约束(导数滤波器和鲁棒函数)(Sun,Roth等2008)。这些技术在Baker,Scharstein等人(2011)和Sun,Roth和Black(2014)的文章中进行了更详细的讨论。 由于估计流体时存在较大的二维搜索空间,大多数算法采用梯度下降和粗到精的连续方法来最小化全局能量函数。这与立体匹配形成了鲜明对比,后者是一个“更简单”的一维视差估计问题,在深度神经网络出现之前,组合优化技术是首选方法。一种应对这种复杂性的方法是从高效的基于块的对应关系开始(Kroeger,Tim-oft et al.2016)。另一种处理大二维搜索空间的方法是将稀疏特征匹配整合到变分公式中,这一方法最初由Brox和Malik(2010a)提出。后来,包括几位作者在内的多个研究者对此进行了扩展。
12稳健的亮度指标(第9.1节,(9.2))也可帮助提高基于窗口的方法的性能(Black和Anandan1996)。
13在Xu、Ranftl和Koltun中可以找到一些例外,这些例外情况表明,没有探索完整的4D成本量。
(2017)和Teed和Deng(2020b)。

图9.8 24种光流算法结果评估,2009年10月,https://vision.middlebury.edu/flow,(Baker,Scharstein等,2009)。通过将鼠标指针移到带下划线的性能评分上,用户可以交互式地查看相应的流场和误差图。点击评分可以在计算结果和真实值之间切换。每个评分旁边都有一个较小的蓝色数字,表示当前列中的相应排名。每列中的最低(最佳)评分以粗体显示。表格按平均排名排序(总体计算了24列,每八个序列各三个区域掩模)。平均排名作为所选度量/统计指标下的性能近似度量。
Weinzaepfel,Revaud等人(2013)的DeepFlow系统使用手工设计(非学习)卷积网络计算初始准密集对应关系,Revaud,Weinza- epfel等人(2015)的EpicFlow系统在变分优化之前添加了边缘和遮挡感知插值步骤。
基于马尔可夫随机场的组合优化方法在贝克、沙尔斯坦等人(2011)最初发布的光流数据库中表现良好,但如今已被深度神经网络超越。这类技术的例子包括格洛克、帕拉吉奥斯等人(2008)开发的方法,他们采用粗到精的策略,使用逐像素的二维不确定性估计,然后用于指导下一层次的细化和搜索。莱姆皮茨基、罗思和罗瑟(2008)利用融合移动(莱姆皮茨基、罗瑟和布莱克2007)来寻找好的解决方案,这些移动是基于基本流算法(霍恩和舒恩克1981;卢卡斯和卡纳德1981)生成的提案。
对这些“经典”的粗到精的能量最小化方法进行了细致的经验分析,详见孙、罗思和布莱克(2014)精心撰写的论文。图9.9a展示了他们研究框架的主要组成部分,包括基于前一层次流动的初始变形(或在最粗层次进行网格搜索),随后是能量最小化的流动更新,最后是一个可选的后处理步骤。在他们的论文中,作者不仅回顾了从1980年代(霍恩和舒恩克1981)到2013年开发的数十种变分(能量最小化)方法,还指出诸如中值滤波后处理等算法细节,往往被先前的研究者忽略,但对结果有重要影响。除了在米德尔伯里流数据集(贝克、沙尔斯坦等人2011)上进行分析外,他们还在较新的Sintel数据集(巴特勒、沃尔夫等人2012)上进行了评估。
精确运动估计领域正以惊人的速度发展,每年都有显著的性能提升。虽然米德尔伯里光流网站(图9.8)仍然是高性能算法的良好资源,但最近的出版物更多地关注(无论是训练还是评估)由巴特勒、沃尔夫等人(2012)开发的MPI Sintel数据集,其中一些样本如Figure9.1e-f所示。一些算法还在KITTI流基准上进行训练和测试(盖格、伦兹和乌尔塔苏恩2012),尽管该数据集侧重于从行驶车辆获取的视频。总体而言,基于学习的算法在使用一个数据集训练后,应用于另一个数据集时仍会遇到困难。17

图9.9迭代粗到精光流估计(Sun,Yang等,2018)©2018 IEEE:(a)“经典”变分(能量最小化)方法(Sun,Roth和Black,2014);(b)较新的神经网络方法,通过端到端深度学习训练(Sun,Yang等,2018)。两幅图均展示了单个层级的粗到精金字塔处理过程,输入为前一层(较粗)计算出的光流,并将细化后的光流传递给下一层更精细的层级。
在过去的十年里,深度神经网络已经成为所有高度智能的组成部分
高效的光流算法,如Janai、G ney等人在综述文章中所述。
(2020,第11章)和Hur和Roth(2020)。一种早期的方法是使用受深度卷积网络启发的非线性聚合,即Weinzaepfel、Revaud等人(2013)的DeepFlow系统,该系统采用手工设计(非学习)的卷积和池化来计算多级响应图(匹配成本),然后使用经典的能量最小化变分框架进行优化。
首个在编码器-解码器网络中使用全深度端到端学习的系统是FlowNetS (Dosovitskiy,Fischer等,2015),该系统基于作者合成的FlyingChairs数据集进行训练。论文还介绍了FlowNetC,该方法采用关联网络(局部成本卷积)。后续的FlowNet 2.0系统利用初始流估计来扭曲图像,然后通过级联编码器-解码器网络进一步优化流估计(Ilg,Mayer等,2017),而后续的研究还涉及遮挡和不确定性建模(Ilg,Saikia等,2018;Ilg,C¸ic¸ek等,2018)。
一种替代方法是将全分辨率网络串联起来,同时使用图像金字塔和流金字塔,并结合粗到精的变形和细化,这一方法最早由Ranjan和Black(2017)在SPyNet论文中提出。Sun、Yang等人(2018,2019)提出的较新的PWC-Net如图Figure9.9b所示,通过首先从每一帧计算特征金字塔,再根据从前一分辨率插值得到的流变形第二组特征,扩展了这一思路。
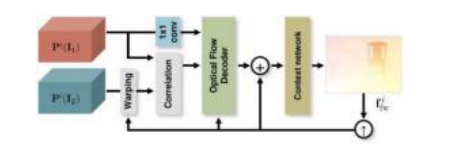
图9.10迭代残差优化光流估计(Hur和Roth 2019)©2019 IEEE。Sun、Yang等人(2018)在Figure9.9bis中提出的从粗到精的级联方法被替换为循环神经网络(RNN),该网络将插值后的较粗层次的光流估计作为下一层更精细层次的变形输入,但每层使用相同的卷积权重。
层级,然后通过特征图之间的点积计算出成本体积,这些特征图最多偏移了d=士4像素。当前层级的精细光流估计是使用多层卷积神经网络生成的,该网络的输入包括成本体积、图像特征以及前一层次插值的光流。最终的情境网络以倒数第二层的光流估计和特征作为输入,并利用扩张卷积赋予网络更广泛的上下文。如果你比较图9.9a–b,你会看到经典和深度粗到精光流估计算法各个处理阶段之间令人愉悦的一致性。18
赫尔和罗斯(2019)开发的一种粗到精的PWC-Net变体是图9.10所示的迭代残差细化网络。与FlowNet 2.0和PWC-Net不同,IRR在每一层都重用了相同的结构和卷积权重,这使得网络可以被“卷起”绘制,如图所示。因此,该网络可以被视为一个简单的递归神经网络(RNN),在每个阶段后对输出流估计进行上采样。除了参数更少外,这种权重共享还提高了准确性。在他们的论文中,作者还展示了如何扩展(加倍)此网络以同时计算前向和后向流以及遮挡情况。
在最近的研究中,Jonschkowski、Stone等人(2020)以PWC-Net为基础架构,系统地研究了训练流估计器的所有组件,采用无监督的方式,即使用没有真实流的常规现实视频,这可以使用更大的训练集(Ahmadi和Patras 2016;Meister、Hur和Roth 2018)。在他们的论文中,Jonschkowski等人系统地比较了光度损失、遮挡估计、自监督和平滑性约束,并分析了
18注意,与其他粗略到精细的变形方法一样,这些算法难以处理快速移动的细小结构,而这些结构在较粗的层次上可能不可见(Brox和Malik2010a)。
其他选择的影响,如预训练、图像分辨率、数据增强和批量大小。他们还提出了四个改进措施,包括成本体积归一化、遮挡估计的梯度停止、在原生流分辨率下应用平滑性以及用于自监督的图像缩放。另一篇近期明确处理遮挡问题的论文是江、坎贝尔等人(2021)。
最近的一个趋势是建模由于均匀和遮挡区域导致的流场估计中的不确定性(Ilg,C¸ic¸ek等,2018)。Yin、Darrell和Yu(2019)开发的HD3网络在多个分辨率级别之间建模对应分布,而Hui和Loy(2020)的LiteFlowNet3网络扩展了他们的小型快速LiteFlowNet2网络(Hui、Tang和Loy,2021),通过成本体积调制和流场变形模块显著提高了精度,同时成本极低。在同一时期的工作中,Hofinger、Rota Bul等人(2020)引入了新的组件,如用采样代替扭曲、智能梯度阻塞和知识蒸馏,这些不仅提高了其流估计的质量,还
可以用于其他应用,例如立体匹配。Tee和Deng(2020b)基于循环网络的思想(Hur和Roth,2019),但不是扭曲特征图,而是预计算一个完整的(W×H)²多分辨率相关体积(循环全对流场变换或RAFT),每次迭代时根据当前的流估计访问该体积。计算一个稀疏的相关体积,仅存储每个参考图像特征的k个最近匹配,可以进一步加速计算(Jiang、Lu等,2021)。
鉴于光流技术的快速演变,哪种方法最好使用?答案高度依赖于具体问题。一种评估方法是跨多个数据集进行测试,如鲁棒视觉挑战赛中所做的那样。在这个综合基准上,RAFT、IRR和PWCall的变体表现良好。另一种方法是根据其特定用途专门评估一种光流算法,并尽可能在特定问题的数据上微调网络。Xue、Chen等人(2019)描述了他们如何在合成降质的Vimeo-90K数据集上微调SPyNet从粗到精的网络以估计任务导向的光流(TOFlow),该方法在三个不同的视频处理任务中优于“更高精度”的网络(甚至优于真实流),这三个任务分别是帧插值(第9.4.1节)、视频去噪(第9.3.4节)和视频超分辨率。通过将合成训练数据定制为目标数据集,也可以显著提高基于学习的光流算法的性能(Sun,
为了节省硅电路并提高光敏度或填充因子,许多移动电话中的CMOS成像传感器采用滚动快门技术,即不同行或列依次曝光。在拍摄快速场景或相机运动时,这可能导致直线变得倾斜或弯曲(例如飞机或直升机的螺旋桨叶片),或者场景中的刚性部分摇晃(也称为果冻效应),例如在动作摄影中相机快速振动时。
为了补偿这些由不同扫描线曝光时间造成的失真,必须精确估计每个像素的光流,而不是有时用于慢动作视频稳定化的全帧参数运动(第9.2.1节)。Baker、Bennett等人(2010年)和Forss n、Ringaby(2010年)是最早研究这一问题的计算机视觉研究人员之一。在他们的论文中,Baker、Bennett等人(2010年)从低频帧间运动
中恢复高频运动场,并用其重新采样每个输出扫描线。Forss n和Ringaby(2010年)使用相机旋转模型进行类似的计算,这需要内参镜头校准。Grundmann、Kwatra等人(2012年)通过混合单应性来建模相机和场景运动,从而消除了这种校准的需求;而Liu、Gleicher
等人(2011年)则使用子空间约束。为了生成高质量的图像拼接结果,还需要精确的滚动快门校正(Zhuang和Tran 2020)。
在一些现代成像系统中,如运动相机,惯性测量单元(IMU)可以提供相机运动的高频估计,但它们无法直接提供深度依赖视差和独立物体运动的估计。因此,最佳的相机内图像稳定器使用IMU数据和复杂的图像处理相结合。20模型化滚动快门对于从运动中获取结构的准确姿态估计也非常重要(Hedborg,Forss n等2012;Kukelova,Albl等2018;Albl,Kukelova等2020;Kukelova,Albl等2020),以及视觉-惯性融合在SLAM中的应用(Patron-Perez,Lovegrove
和Sibley 2015;Schubert,Demmel等2018),这些内容将在第11.4.2节和第11.5节中讨论。
到目前为止,我们已经将运动估计看作是一个两帧问题,目标是计算出一个运动场,使一个图像中的像素与另一个图像中的像素对齐。实际上,运动估计通常应用于视频中,在视频中可以使用一整序列的帧来执行这个任务。

图9.11空间-时间体积的切片(Szeliski1999a)©1999 IEEE:(a-b)花园序列中的两帧;(c) a横向切片穿过完整的时空体积,箭头指示估计流动的关键帧位置。请注意,花园序列的颜色不正确;正确的颜色(黄色花朵)显示在图9.13中。
一种经典的多帧运动处理方法是使用定向或可转向滤波器(Heeger1988)对时空体进行滤波,类似于定向边缘检测(第3.2.3节)。图9.11展示了常用花园序列中的两帧,以及通过堆叠所有视频帧创建的三维体积的水平切片。由于像素运动主要为水平方向,因此可以清楚地看到各个(纹理)像素轨迹的斜率,这对应于它们的水平速度。时空滤波利用每个像素周围的三维体积来确定其在时空中的最佳方向,这直接对应于像素的速度。
不幸的是,为了在图像的各个位置获得相对准确的速度估计,时空滤波器具有较大的范围,这严重降低了其在运动不连续处的估计质量。(这个问题同样存在于基于二维窗口的运动估计器中。)一种替代全时空滤波的方法是估算更多的局部时空导数,并在全局优化框架内使用这些导数来填补无纹理区域(Bruhn,Weickert,和Schn rr2005;Govindu2006)。
另一种选择是同时估计多个运动估计,同时可选地推理遮挡关系(Szeliski 1999a)。图9.11c示意性地展示了一种潜在的方法。水平箭头表示关键帧s的位置,在这些位置进行运动估计,而其他切片则表示视频帧,其颜色与通过插值关键帧预测的颜色相匹配。运动估计可以被表述为一个全局能量最小化问题,该问题同时最小化关键帧与其他帧之间的亮度兼容性和流兼容性项,此外还使用了稳健的平滑项。
多视图框架对于刚性场景运动来说可能更加合适
(多视图立体)(第12.7节),其中每个像素的未知数是视差和遮挡关系,可以直接从像素深度确定(Szeliski1999a;Kol- mogorov和Zabih2002)。然而,它也适用于一般运动,通过增加遮挡关系模型,如Hur和Roth(2017)的MirrorFlow系统所示。
以及多帧版本(Janai、Guney等人,2018;Neoral、ochman和Matas2018;
Ren、Gallo等人,2019)。
视频降噪是去除电影和视频中的噪声和其他伪影(如划痕)的过程(Kokaram2004;Gai和Kang2009;Liu和Freeman2010)。与单张图像降噪不同,后者仅能利用当前画面的信息,而视频降噪器可以从相邻帧中平均或借用信息。然而,为了在不引入模糊或抖动(不规则运动)的情况下实现这一目标,它们需要精确的逐像素运动估计。一种方法是使用任务导向的流,其中流网络被专门调整以端到端提供最佳降噪性能(Xue,Chen等2019)。
练习9.6列出了所需的一些步骤,包括判断当前运动估计是否足够准确,可以与其他帧进行平均。尽管一些最近的论文继续将流估计作为多帧去噪流程的一部分(Tassano、Delon和Veit 2019;Xue、Chen等2019),但其他研究要么将不同帧中的相似块拼接在一起(Maggioni、Boracchi等2012),要么将小部分帧组合成一个深度网络,该网络从未明确估计运动表示(Claus和van Gemert 2019;Tassano、Delon和Veit 2020)。一种更通用的视频增强和恢复方法——视频质量映射——也最近开始受到关注(Fuoli、Huang等2020)。
在许多情况下,视觉运动是由场景中不同深度的少量物体的移动引起的。在这种情况下,如果将像素分组为适当的物体或层,则可以更简洁地描述(并更可靠地估计)像素运动(Wang和Adelson1994)。
图9.12示意性地展示了这种方法。这一序列中的运动是由棋盘背景的平移和前景手部的旋转引起的。完整的运动序列可以从前景和背景元素的外观中重建,这些元素可以表示为透明抠像图像(精灵或视频

图9.12分层运动估计框架(王和阿德森1994)©1994 IEEE:最上面两行描述了两个层次,每个层次包含一个强度(颜色)图像、一个透明度(黑色=透明)的遮罩以及一个参数化的运动场。这些层次通过不同量的运动合成,以重现视频序列。
(对象)和对应于每一层的参数化运动。将这些层按从后向前的顺序置换和合成(第3.1.3节)可重现原始视频序列。
分层运动表示不仅能够生成紧凑的表示(Wang和Adelson 1994;Lee、Chen等1997),还能充分利用多个视频帧中的信息,并准确建模运动不连续处像素的外观。这使得它们特别适合用于基于图像的渲染(第14.2.1节)(Shade、Gortler等1998;Zitnick、Kang等2004),以及对象级别的视频编辑。
为了计算视频序列的分层表示,王和阿德森(1994)首先在一组非重叠的块上估计仿射运动模型,然后使用k均值聚类这些估计值。接着,他们交替进行像素分配到各层和使用分配的像素重新计算每层的运动估计,这一技术最初由达雷尔和彭特兰(1991)提出。一旦每个帧的参数化运动和逐像素层分配独立计算完成,通过将所有帧中的不同层部分进行扭曲和合并来构建分层。中值滤波用于生成对小强度变化具有鲁棒性的清晰复合层,

图9.13分层运动估计结果(Wang和Adelson1994)©1994 IEEE。
以及推断各层之间的遮挡关系。图9.13展示了这一过程在花园序列上的结果。你可以看到其中一个帧的初始和最终层分配,以及合成流和带有相应流矢量叠加的透明遮罩层。
在后续研究中,魏斯和阿德森(1996)使用正式的概率混合模型来推断最优层数和每像素的层分配。魏斯(1997)进一步推广了这种方法,用平滑正则化的每像素运动估计替换了每层的仿射运动模型,这使得系统能够更好地处理弯曲和起伏的层,如大多数真实世界序列中所见。
然而,上述方法仍然区分了先估计运动和层分配,然后再估计层颜色。在贝克、斯泽利斯基和阿南丹(1998)描述的系统中,生成模型被推广以适应现实世界的刚性运动场景。每一帧的运动使用三维相机模型来描述,而每一层的运动则通过三维平面方程加上每个像素的残余深度偏移(即平面加视差表示(第2.1.4节))来描述。初始层估计的过程类似于王和阿德森(1994)的方法,只是使用了刚性平面运动(单应矩阵)而不是仿射运动模型。然而,最终的模型优化通过最小化重新合成的运动序列与观察到的运动序列之间的差异,联合重新优化层像素颜色和不透明度值Ll以及三维深度、平面和运动参数zl、nl和Pt(贝克、斯泽利斯基和阿南丹1998)。
图9.14展示了使用该算法获得的最终结果。如你所见,运动边界和层分配比图9.13中的要清晰得多。由于每个像素的深度偏移,单个层的颜色值也比使用仿射或平面运动模型得到的更锐利。而贝克、斯泽利斯基的原始系统,

图9.14分层立体重建(Baker、Szeliski和Anandan1998)©1998
IEEE: (a)第一张输入图像;(b)最后一张输入图像;(c)初始分割为六层;(d)和(e)六层精灵;(f)平面精灵的深度图(颜色越深表示距离越近);前一层(g)残差深度估计前;(h)残差深度估计后。请注意,花园序列的颜色不正确;正确的颜色(黄色花朵)如图9.13所示。
Anandan(1998)要求对像素进行粗略的初始分层,Torr、Szeliski和Anandan(2001)描述了用于初始化该系统并确定最佳层数的自动贝叶斯技术。
层次运动估计仍然是一个活跃的研究领域。2000年代的代表性论文包括(Sawhney和Ayer 1996;Jojic和Frey 2001;Xiao和Shah 2005;Kumar、Torr和Zisserman 2008;Thayananthan、Iwasaki和Cipolla 2008;Schoenemann和Cremers 2008),而更近期的论文则包括(Sun、Sudderth和Black 2012;Sun、Wulff等2013;Sun、Liu和Pfister 2014;Wulff和Black 2015)以及(Sevilla-Lara、Sun等2016),这些研究共同实现了语义分割和运动估计。
层次并不是将分割引入运动估计的唯一方法。已经开发了大量算法,在估计光流向量和将其分割为连贯区域之间交替进行(Black和Jepson 1996;Ju、Black和Jepson 1996;Chang、Tekalp和Sezan 1997;M min和P rez 2002;Cremers和Soatto 2005)。其中一些技术依赖于首先分割输入的颜色图像,然后
估计每个片段的运动,以生成连贯的运动场,同时建模遮挡(Zitnick,Kang等2004;Zitnick,Jojic和Kang 2005;Stein,Hoiem和Hebert 2007;Thayananthan,Iwasaki和Cipolla 2008)。事实上,视频中连贯运动部分的分割已经发展成为一个独立的主题,即视频对象分割,我们将在第9.4.3节中研究。
帧插值是运动估计的一个广泛应用,通常在硬件中实现,以匹配输入视频与显示器的实际刷新率,在这种情况下,需要从前后帧中插值出新颖的中间帧信息。如果能够在每个未知像素位置计算出准确的运动估计,可以获得最佳效果。然而,除了计算运动外,遮挡信息也至关重要,以防止移动前景物体污染特定像素的颜色,这些物体可能会遮挡前一帧或后一帧中的某个像素。
更详细地考虑图9.11c,并假设箭头表示我们希望插值的帧之间的关键帧。该图中条纹的方向编码了各个像素的速度。如果在图像I0中的位置x0处获得的运动估计u0与在图像I1中的位置x0 + u0处获得的运动估计相同,则称这些流向量是一致的。这个运动估计可以转移到生成图像It中的位置x0 + tu0,其中t∈(0;1)是插值的时间。最终的颜色值可以在像素x0 + tu0处通过线性混合计算得出,
它(x0 + tu0)=(1 - t)I0(x0)+ tI1(x0 + u0)。 (9.59)
然而,如果对应位置的运动矢量不同,则必须使用某种方法来确定哪个是正确的,以及哪张图像包含被遮挡的颜色。实际的推理过程比这更为复杂。例如,基于Shade、Gortler等人(1998)和Zitnick、Kang等人(2004)早期深度图插值工作的插值算法,被Baker、Scharstein等人(2011)在流评估论文中采用。Mahajan、Huang等人(2009)提出了一种更高质量的帧插值算法,该算法基于梯度重建。帧插值任务的准确性有时也被用来衡量运动估计算法的质量(Szeliski 1999b;Baker、Scharstein等人2011)。
最近的帧插值技术使用深度神经网络作为其架构的一部分。一些方法使用时空卷积(Niklaus,Mai和Liu 2017),而其他方法则使用DNN计算双向光流(Xue,Chen等人2019)。

图9.15深度特征视频插值网络(Niklaus和Liu 2020)©2020 IEEE。该多阶段网络首先计算双向流,使用特征金字塔编码每一帧,然后通过软并融合这些特征进行变形和组合。组合后的特征随后输入最终的图像合成网络(解码器)。
然后使用上下文特征(Niklaus和Liu 2018)或软可见性图(Jiang、Sun等2018)将两个原始帧的贡献结合起来。Niklaus和Liu(2020)的系统将输入帧编码为深度多分辨率神经特征,通过双向流前向扭曲这些特征,使用softmax分散法结合这些特征,最后使用一个最终的深度网络解码这些组合特征,如图9.15所示。类似的架构也可以用于从单张静态图像创建具有时间纹理的循环视频(Holynski、Curless等2021)。其他最近开发的帧插值网络包括Choi、Choi等(2020)、Lee、Kim等(2020)、Kang、Jo等(2020)和Park、Ko等(2020)。
层状运动的特殊情况是透明运动,通常由窗户和相框中看到的反射引起(图9.16和9.17)。
该领域的早期研究中,一些工作通过估计运动成分(Shizawa和Mase 1991;Bergen、Burt等1992;Darrell和Simoncelli 1993;Irani、Rousso和Peleg 1994)或将单个像素分配到竞争的运动层来处理透明运动,这适用于部分被精细遮挡物(如树叶)遮挡的场景。然而,为了准确分离真正透明的层次,需要一个更好的反射运动模型。由于光线既从玻璃表面反射又透过玻璃表面传播,正确的反射模型是累加式的,每个移动层都会对最终图像贡献一定的强度(Szeliski、Avidan和Anandan 2000)。

图9.16光线从相框透明玻璃反射:(a)输入序列中的第一张图像;(b)主导运动层最小合成;(c)次要运动残差层最大合成;(d–e)最终估计的图像和反射层原始图像来自Black和Anandan(1996),而分离的层来自Szeliski、Avidan和Anandan(2000)©2000 IEEE。
如果已知各层的运动,恢复各层图像就变成了一个简单的约束最小二乘问题,其中各层图像被限制为正值,饱和像素则对总和值提供了不等式约束。然而,这个问题可能会受到长时间低频模糊的影响,特别是当某一层缺乏暗(黑色)像素或运动是单向时。在他们的论文中,Szeliski、Avidan和Anandan(2000)指出,通过交替稳健计算运动层并随后对层强度做出保守(上限或下限)估计,可以同时估计运动和层值。最终的运动和层估计可以通过梯度下降法在类似于Baker、Szeliski和Anandan(1998)提出的联合约束最小二乘公式上进行优化,其中过度合成算子被替换为加法。
图9.16和9.17显示了将这些技术应用于两个具有反射的图像帧的结果。请注意,在第二个序列中,反射光的量与透射光(女孩的照片)相比非常低,然而算法仍然能够恢复两层。

图9.17透明运动分离(Szeliski、Avidan和Anandan2000)©2000
IEEE:(a)输入序列的第一幅图像;(b)主导运动层最小合成;(c)第二-
最大复合的动态残差层;(d-e)最终估计的图像和反射层。注意,(c)和(e)中的反射层的强度被加倍,以更好地显示其结构。
不幸的是,Szeliski、Avidan和Anand(2000)使用的简单参数化运动模型仅适用于平面反射器和浅景深场景。这些技术扩展到曲面反射器和深度显著的场景的研究也已开展(Swaminathan、Kang等2002;Criminisi、Kang等2005;Jacquet、Hane等2013),以及更复杂三维深度场景的扩展研究(Tsin、Kang和Szeliski 2006)。虽然用于评估光流技术的运动序列也开始包括反射和透明度(Baker、Scharstein等2011;Butler、Wulff等2012),但它们提供的地面真实流估计仅包含每个像素的主要运动,例如忽略雾气和反射。
在最近的研究中,辛哈、科普夫等人(2012)使用两层具有不同深度和反射率的相机捕捉到的三维场景中的反射进行建模,然后利用这些反射生成基于图像的渲染(新颖视图合成),我们将在第14.2.1节中详细讨论。科普夫、兰古特等人(2013)扩展了该系统的建模和渲染组件,以恢复每层的彩色图像梯度,然后使用梯度域渲染重建新颖视图。薛、鲁宾斯坦等人(2015)通过引入梯度稀疏先验,扩展了这些模型,以实现透过窗户和围栏时的无障碍摄影。关于这一主题的更近期论文包括杨、李等人(2016)、南多里亚、埃尔加里布等人(2017)和刘、赖等人(2020a)。双像素成像传感器的出现,最初设计用于快速对焦,也可以通过将梯度分离到不同的深度平面来消除反射(普纳普拉特和布朗2019)。

图9.18来自密集标注视频分割(DAVIS)数据集的样本序列©Pont-Tuset,Perazzi等人(2017)。DAVIS 2016数据集(a)仅包含前景-背景分割(红色区域),而DAVIS 2017数据集(b)则在每个序列中包含多个标注对象(亮色区域)。
虽然所有这些技术对于分离或消除作为相干图像出现的反射都很有用,但更复杂的三维几何形状通常会产生空间分布的镜面反射(第2.2.2节),这不适合基于层的表示。在这种情况下,表面光场(第14.3.2节和图14.13)和神经光场(第14.6节和图14.24b)等光场表示可能更为合适。
正如我们在本章中所见,准确估计运动通常需要将视频分割成连贯移动的区域或对象,并正确建模遮挡。将视频片段分割成连贯的对象是静态图像分割的时间类比,我们在第7.5节中研究过。除了提供更准确的运动估计外,视频对象分割还支持多种编辑任务,如对象移除和插入(第10.4.5节),以及视频理解和解释。
虽然前景和背景层的分割研究已经进行了很长时间(Bergen,Anandan等,1992;Wang和Adelson,1994;Gorelick,Blank等,2007;Lee和Grauman,2010;Brox和Malik,2010b;Lee,Kim和Grauman,2011;Fragkiadaki,Zhang和Shi,2012;Papazoglou和Ferrari,2013;Wang,Shen和Porikli,2015;Perazzi,
王等人(2015)引入了戴维斯(密集注释视频分割),佩拉齐、庞特-图塞等人(2016)的贡献极大地加速了该领域的研究。图9.18a展示了原始戴维斯2016数据集的一些帧,其中第一帧带有前景像素掩模(显示为红色),任务是估计其余帧的前景掩模。戴维斯2017数据集(庞特-图塞、佩拉齐等人,2017)将视频片段数量从50增加到150,增加了更多具有挑战性的元素,如运动模糊和前景遮挡,并且最重要的是,每个序列中添加了一个以上的标注对象(图9.18b)。
视频对象分割算法,如OSVOS (Caelles,Maninis等,2017)、FusionSeg (Jain,Xiong,和Grauman,2017)、MaskTrack (Perazzi,Khoreva等,2017)和SegFlow (Cheng,Tsai等,2017),通常包括一个深度逐帧分割网络以及用于连接和优化分割的运动估计算法。一些方法(Caelles,Maninis等,2017;Khoreva,Benenson等,2019)还基于第一帧注释对分割网络进行微调。最近的方法则侧重于提高流水线的计算效率(Chen,Pont-Tuset等,2018;Cheng,Tsai等,2018;Wug Oh,Lee等,2018;Wang,Zhang等,2019;Meinhardt和Leal-Taix,2020)。
自2017年起,每年都会与CVPR联合举办关于DAVIS数据集的挑战赛和研讨会。近年来,挑战赛新增了带有较弱注释/涂鸦的分割任务(Caelles,Montes等人,2018年),以及完全未监督的分割任务,算法能够计算视频帧的时间关联分割(Caelles,Pont-Tuset等人,2019年)。此外,还有一个更新、更大的数据集,名为YouTube-VOS (Xu,Yang等人,2018年),该数据集也有自己的挑战赛和排行榜。关于这一主题发表的论文数量持续很高。最近工作的最佳来源是https://davischallenge.org和https://youtube-vos.org上的挑战排行榜,这些排行榜附有简短的技术描述文章,还有大量会议论文,通常标题中包含“视频对象分割”。
计算机视觉在视频分析中最广泛的应用之一是视频对象跟踪。这些应用包括监控(Benfold和Reid2011)、动物和细胞跟踪(Khan、Balch和Dellaert2005)、运动员跟踪(Lu、Ting等人2013)以及汽车安全(Janai、G ney等人2020,第6章)。
我们在前面的章节中已经讨论了更简单的跟踪示例,包括第7.1.5节中的特征(补丁)跟踪和第7.3节中的轮廓跟踪。

图9.19视觉目标跟踪(Smeulders,Chu等人,2014)©2014 IEEE:(a)高级模型显示主要跟踪器组件;(b)一些跟踪区域表示,包括单个边界框、轮廓、斑点、基于块的、稀疏特征、部件和多个边界框。
此类技术的实验评价包括Lepetit和Fua(2005)、Yilmaz、Javed和Shah(2006)、Wu、Lim和Yang(2013)以及Janai、Gnei等人(2020,第6章)。
了解跟踪技术的一个很好的起点是斯梅尔德斯、朱等人(2014)的调查和教程,这也是最早的大规模跟踪数据集之一,包含超过300个视频片段,时长从几秒到几分钟不等。图9.19a展示了在线跟踪系统中通常存在的几个主要组件,包括选择形状、运动、位置和外观的表示方法,以及相似度测量、优化和可选的模型更新。图9.19b展示了一些用于表示形状和外观的选择,包括单个边界框、轮廓、补丁、特征和部分。
论文包括对先前调查和技术的讨论,以及数据集、评估指标和上述模型选择。随后,它将一些知名和较新的算法分类到一个分类体系中,该体系包括固定模板的简单匹配、扩展和约束(稀疏)外观模型、判别分类器和基于检测的跟踪。所讨论和评估的算法包括由贝克和马修斯(2004年)实现的KLT、均值漂移(科马尼丘和米尔2002年)和片段基(亚当、里夫林和辛莫尼2006年)跟踪、在线PCA外观模型(罗斯、林等人2008年)、稀疏基(梅和凌2009年)以及使用核化结构输出支持向量机的Struct(哈雷、戈洛杰茨等人2015年)。
大约在同一时期(2013年),一系列关于单目标短期跟踪的年度挑战和研讨会开始,称为VOT(视觉对象跟踪)。21在他们描述评估方法的期刊论文中,Kristan、Matas等人(2016)评估了最近的跟踪器,并发现结构化变体以及核化相关滤波器(KCF)的扩展,
最初由亨里克斯、卡塞罗等人(2014)开发,表现最佳。这一时期的其他具有高度影响力的论文包括(贝尔蒂内托、瓦尔马德雷等人2016a,b;丹内尔詹、罗宾逊等人2016)。自那时起,深度网络在视觉物体跟踪中发挥了关键作用,通常使用孪生网络(第5.3.4节;布罗姆利、居约等人1994;乔普拉、哈德塞尔和勒昆2005)将被跟踪的区域映射到神经嵌入中。关于更近期跟踪算法的列表和描述,可以在伴随VOT挑战赛和研讨会的年度报告中找到,最近的一份是克里斯坦、莱昂德尼斯等人(2020)。
与单目标VOT挑战和研讨会并行,多目标跟踪作为KITTI视觉基准的一部分被引入(Geiger,Lenz,和Urtasun 2012),Leal-Taix,Milan等人(2015)也开发了一个独立的基准,并推出了一系列挑战,最近的结果由Dendorfer,O ep等人(202)描述。Luo,Xing等人(2021)对2016年之前的多目标跟踪论文进行了综述。简单快速的多目标
跟踪器包括Bergmann、Meinhardt和Leal-
Taix(2019
)和Zhou、Koltun和Kr henb hl(2020)
。然而,直到最近,追踪
数据集主要关注人、车辆和动物。为了扩大可追踪对象的范围,Dave、Khurana等人(2020)创建了TAO(跟踪任何物体)数据集,包含2,907个视频,这些视频首先由用户标记所有移动的物体,然后将这些物体分类到833个类别中。
虽然在本节中,我们主要关注的是物体跟踪,其主要目标是在连续的视频帧中定位一个物体,但也可以同时进行跟踪和分割(Voigtlaender,Krause等2019;Wang,Zhang等2019),或者使用可变形模型跟踪非刚性变形物体,如T恤(Kambhamettu,Goldgof等2003;White,Crane和Forsyth 2007;Pilet,Lepetit和
Fua2008;Furukawa和Ponce2008;Salzmann和Fua2010)或RGB-D流(Bo i,
Zollh等人,2020年
;Bo i等人,Palafox等人,2020
年,2021年)。最近的TrackFormer论文
Meinhardt、Kirillov等人(2021)对多目标跟踪和分割的最新工作进行了很好的综述。
一些最早的运动估计算法是为运动补偿视频编码开发的(Netravali和Robbins,1979),这些技术继续被用于现代编码标准,如MPEG、H.263和H.264 (Le Gall,1991;Richardson
2003年)。在计算机视觉领域,这一分支最初被称为图像序列分析(黄1981)。一些早期的开创性论文包括霍恩和舒恩克(1981)以及纳格尔和恩克尔曼(1986)开发的变分方法,以及卢卡斯和卡纳德(1981)开发的基于块的平移对齐技术。这些算法的层次化(从粗到细)版本由昆(1984)、阿南丹(1989)和伯根、阿南丹等人(1992)开发,尽管它们也长期用于视频编码中的运动估计。
Rehg和Witkin(1991)、Fuh和Maragos(1991)以及Bergen、Anandan等人(1992)将平移运动模型推广到仿射运动,Shashua和Toelg(1997)以及Shashua和Wexler(2001)则将其推广到二次参考曲面——详见Baker和Matthews(2004)的综述。这些参数化运动估计算法在视频摘要(Teodosio和Bender 1993;Irani和Anandan 1998)、视频稳定(Hansen、Anandan等人1994;Srinivasan、Chellappa等人2005;Matsushita、Ofek等人2006)和视频压缩(Irani、Hsu和Anandan 1995;Lee、Chen等人1997)中得到了广泛应用。关于参数化图像配准的综述包括Brown(1992)、Zitov‘aa和Flusser(2003)、Goshtasby(2005)以及Szeliski(2006a)的研究。
光学流算法的总体调查和比较包括Aggar- wal和Nandhakumar(1988)、Barron、Fleet和Beauchemin(1994)、Otte和Nagel(1994)、Mitiche和Bouthemy(1996)、Stiller和Konrad(1999)、McCane、Novins等人(2001)等人的研究,
Szeliski(2006a)、Baker、Scharstein等人(2011)、Sun、Yang等人(2018)、Janai、G ney等人
等(2020),以及赫尔和罗斯(2020)。匹配基元的主题,即在匹配前使用滤波或其他技术预处理图像,在多篇论文中有所讨论(阿南丹1989;伯根、阿南丹等人1992;沙尔斯坦1994;扎比和伍德菲尔1994;考克斯、罗伊和欣戈拉尼1995;维奥拉和威尔斯三世1997;内加达里普尔1998;金、科洛莫戈罗夫和扎比2003;贾和唐2003;帕彭贝格、布鲁恩等人2006;塞茨和贝克
2009年)。Hirschm ller和Scharstein(2009年)比较了其中一些方法并报告
根据他们在曝光差异场景中的相对表现。
贝克、沙尔斯坦等人(2011)首次发布了用于评估光流算法的大规模基准测试,这促进了估计算法质量的迅速提升。尽管大多数表现最佳的算法使用了稳健的数据和平滑度规范,如L1或TV以及连续变分优化技术,但一些算法采用了离散优化或分割方法(帕彭贝格、布鲁恩等人2006;特罗宾、波克等人2008;徐、陈和贾2008;莱姆皮茨基、罗斯和罗瑟2008;维尔伯格、特罗宾等人2009;雷和杨2009;韦德尔、克雷默斯等人2009)。
太阳2012)数据集进一步加速了光流算法的进步。过去十年中发表的重要论文包括温扎普费尔、雷沃等人(2013),孙、罗斯和布莱克(2014),雷沃、温扎普费尔等人(2015),伊尔格、迈耶等人(2017),徐、兰夫特和科尔图恩(2017),孙、杨等人(2018,2019),赫尔和罗斯(2019),以及蒂德和邓(2020b)。关于过去十年光流论文的综述,可参见孙、杨等人(2018),贾奈、格内伊等人(2020),以及赫尔和罗斯(2020)。
关于视频对象分割和视频对象跟踪的阅读起点是最近与这些主题的主要数据集和挑战相关的研讨会(Pont-Tuset,Perazzi等人,2017;Xu,Yang等人,2018;Kristan,Leonardis等人,2020;Dave,Khurana等人,2020;Dendorfer,O ep等人,2021)。
例9.1:相关性。实现并比较以下相关性算法的性能:
平方差之和(9.1)
稳健差异的总和(9.2)
绝对差值之和(9.3)
•偏置增益补偿平方差(9.9)
•常规交叉相关(9.11)
?上述版本的窗口(9.22–9.23)
基于傅里叶的上述措施的实现(9.18–9.20)
·相位相关(9.24)
?梯度互相关(Argyriou和Vlachos,2003)。
比较几种算法在不同运动序列上的表现,这些序列包含不同程度的噪声、曝光变化、遮挡和频率变化(例如,高频纹理如沙子或布料,以及低频图像如云朵或运动模糊视频)。一些具有光照变化和真实对应关系(水平运动)的数据集可以在https://vision.middlebury.edu/stereo/data网站上找到(2005年和2006年的数据集)。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








