最短路在实际中有很多应用。最短路的路劲一般不再是路径上的数目,而是路径边上的权值之和。所以最短路径都是用在带权有向图上面的。在最短路径方面,有两个著名的算法:Dijkstra算法和Floyd算法。
1:1.Dijkstra算法-从某个点到其余各点的最短路径(贪心算法)
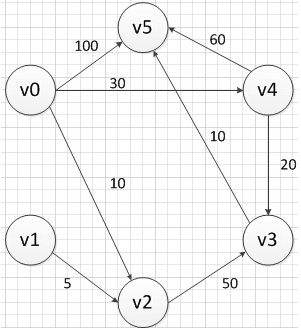
下面根据例子实际说明一下:
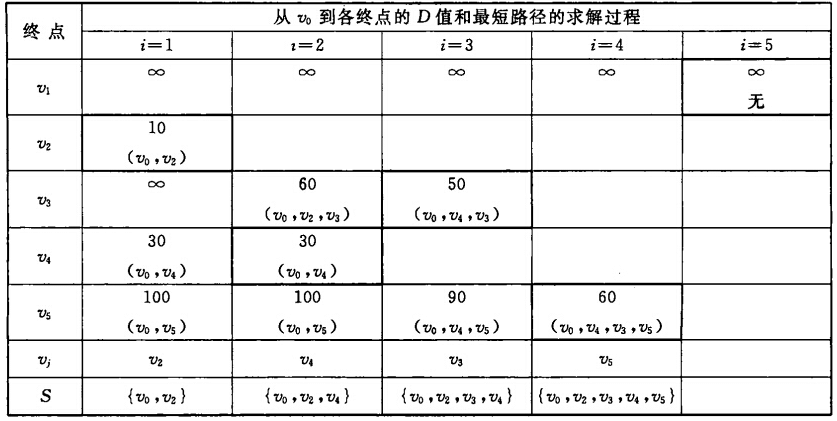
- 一开始我们初始化已选择点集S,我们假设源点为v0,所以先把v0加入S,此时S = {v0}。
- 我们首先遍历除v0之外的所有点,发现v0无法直接到达v1和v3,所以距离为∞。而其他三个点中,到v2点的距离最近,此时我们选择v2加入S,此时S = {v0,v2}。
- 接下来再一次遍历除S内元素之外的所有点。我们可以知道,如果想知道v0到vk的最短距离,则最短距离有两种情况:
(1):v0到vk上的权值。
(2):或者是之间经历了其他顶点,假设经历了一个顶点vj,则最短距离 = v0到vj的最短路径 + vj到vk上的权值。而这个vj就是我们加入到集合S里面的顶点。
所以我们开始更新第一次的路径长度结果,发现通过新加入的点(即v2),我们可以到达v3,此时路径长度 = v0到v2的权值 + v2到v3权值 = 60。而其他点的路径长度没有被更新或者经历了v2后的路径长度并不比更新前的小。最后我们找到路径长度最短的点v4,加入S,此时S = {v0,v2,v4}。
4.再次按照3中的形式进行遍历S之外的点。 此时我们看到加入了v4后,我们到达v3的路径长度被缩短到了50,这个50 = v0到v4的权值 + v4到v3权值,而v0到v4的权值已经被记录过,所以可以直接使用,所以这个距离很容易就被求出。接下来v5的长度更新和v3一样,就不在详述了,最后找到路径长度最短的点v3,加入S,此时S = {v0,v2,v4,v3}。
5. 再次按照3中的形式进行遍历S之外的点。更新了v5的路径长,找到路径长度最短的点v5,加入S,此时S ={v0,v2,v4,v3,v5}。而此时我们发现,只剩下v1,但是从源点v0到v1的距离依然是∞,说明v0没有和v1连通。此时我们将v1加入S,这时集合S的长度 = 顶点数 = 6,算法结束。
源代码如下:
//scdn博客地址 :http://blog.csdn.net/u010006643/article/details/45693401
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
#define MAX 100
#define INT_MAX 10000
#define max(x,y)(x>y?x:y)
typedef struct
{
int matrix[100][100];
int num;
}Graph;
int initNode = 0;
int* shortPath = NULL;
int* S = NULL;
Graph example;
int initGraph()
{
int i,j;
for(i = 0; i < MAX; i++){
for (j = 0; j < MAX; j++)
{
example.matrix[i][j] = INT_MAX;
}
}
example.num = 0;
}
void createPoint()
{
int i, j, val;
initGraph();
while(cin>>i>>j>>val)
{
if(0 == i && 0 == j)
break;
example.matrix[i][j] = val;
example.num = max(example.num,i);
example.num = max(example.num,j);
}
}
void printResult()
{
cout<<"---------------"<<endl;
for (int i = 0; i <= example.num; ++i)
{
if(i != initNode)
cout<<initNode<<"->"<<i<<":"<<shortPath[i]<<" "<<endl;
}
}
void dijkstra()
{
int i, j;
shortPath = new int[example.num + 1];
S = new int[example.num + 1];
int count = 0;
int nowProp;
int minPoint,minval;
for(i = 0; i <= example.num; i++)
{
S[i] = -1;
shortPath[i] = INT_MAX;
}
S[initNode] = 1;
count++;
nowProp = initNode;
while(count <= example.num + 1)
{
minPoint = -1, minval = INT_MAX + 1;
for(i = 0; i <= example.num; i++)
{
if(S[i] != 1)
{
if(example.matrix[initNode][i] < shortPath[i])
{
shortPath[i] = example.matrix[nowProp][i];
}
if(example.matrix[nowProp][i] + shortPath[nowProp] < shortPath[i])
{
shortPath[i] = example.matrix[nowProp][i] + shortPath[nowProp];
}
if(shortPath[i] < minval)
{
minval = shortPath[i];
minPoint = i;
}
}
}
S[minPoint] = 1;
nowProp = minPoint;
count++;
}
}
int main(int argc, char const *argv[])
{
initNode =0;
createPoint();
dijkstra();
printResult();
return 0;
}
//0 2 10 0 4 30 0 5 100 1 2 5 2 3 50 3 5 10 4 5 60 4 3 20 0 0 02.Floyd算法-每对点之间的最短路径(动态规划)
Floyd算法主要的是动态规划的思想(下面的介绍来自于这篇博客)。
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
算法描述:
1. 从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
2. 对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
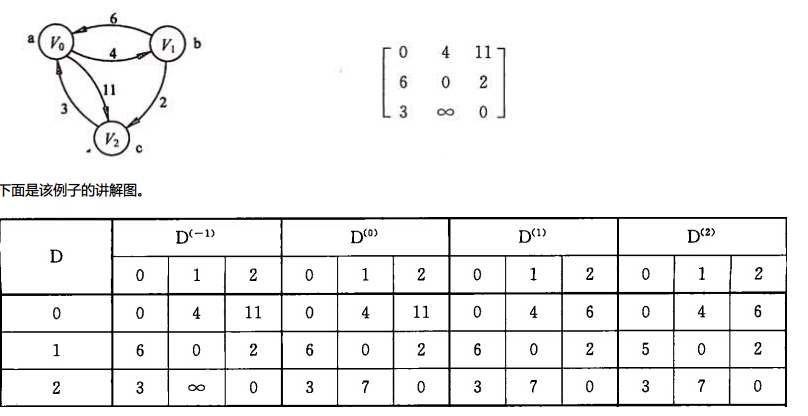
我觉得上面的介绍已经基本上差不多了,下面是一个带权有向图和它的邻接矩阵。
(1)D(−1): 邻接矩阵的初始状态。
(2)D(0): 此时我们对于节点0,检查Dis(i,0) + Dis(0,j) < Dis(i,j)是否成立。 循环后我们发现Dis(2,0) + Dis(0,1) = 7 < Dis(2,1) = ∞,所以替换掉 Dis(2,1)=7。
(3)D(1) : 按照2里面的方法,我们发现Dis(0,1) + Dis(1,2) = 6 < Dis(0,2) = 11。替换掉Dis(0,2) 。重复该步骤,直到循环结束。
而根据图我们可以知道这个主程序是三层循环,所以时间复杂度为O(n3)。但是Dijkstra算法只是从一个源点到其他各点的最短路径,而如果找寻所有点的话,还是需要一个外循环的,所以其实从这个角度看,Dijkstra和Floyd的时间复杂度可以说是一样的,只不过Floyd的思想稍微简单一些。
代码如下:
//scdn博客地址 :http://blog.csdn.net/u010006643/article/details/45693401
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
#define MAX 100
#define INT_MAX 10000
#define max(x,y)(x>y?x:y)
typedef struct{
int matrix[MAX][MAX]; //邻接矩阵
int num;// 最大的顶点数
}Graph;
Graph example;
void initGraph()
{
int i, j;
for(i = 0; i < MAX; i++)
{
for(j = 0; j < MAX; j++)
{
example.matrix[i][j] = INT_MAX;
example.matrix[j][j] = 0;
}
}
example.num = 0;
}
void createPoint()
{
int i , j, val;
initGraph();
while(cin>>i>>j>>val)
{
if(0 == i && 0 == j)break;
example.matrix[i][j] = val;
example.num = max(example.num, i);
example.num = max(example.num, j);
}
}
void printResult()
{
cout<<"----------------"<<endl;
for (int i = 0; i <= example.num; ++i)
{
for (int j = 0; j <= example.num; ++j)
{
cout<<example.matrix[i][j]<<" ";
}
cout<<endl;
}
}
void Floyd()
{
int i, j, k;
for(k = 0; k <= example.num; k++)
{
for(i = 0; i <= example.num; i++)
{
for ( j = 0; j <= example.num; j++)
{
if(example.matrix[i][k] + example.matrix[k][j] < example.matrix[i][j])
{
example.matrix[i][j] = example.matrix[i][k] + example.matrix[k][j];
}
}
}
}
}
int main()
{
createPoint();
Floyd();
printResult();
return 0;
}
//0 1 4 0 2 11 1 0 6 1 2 2 2 0 3 0 0 0







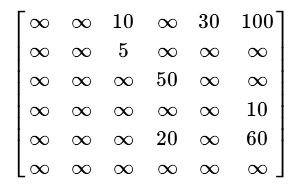















 112
112

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








