黄金分割法是包围策略的经典用例。算法思路为:假定目标函数
f
(
x
)
f(x)
f(x)最优解
x
0
x_0
x0含于长度为
λ
\lambda
λ的区间
(
a
0
,
b
0
)
(a_0,b_0)
(a0,b0)内。在区间内插入两个备选点
a
1
′
,
b
1
′
∈
(
a
0
,
b
0
)
a'_1,b'_1\in(a_0,b_0)
a1′,b1′∈(a0,b0),使得
a
1
′
<
b
1
′
a'_1<b'_1
a1′<b1′且
a
1
′
−
a
0
=
b
0
−
b
1
′
=
ρ
(
b
0
−
a
0
)
=
ρ
λ
a'_1-a_0=b_0-b'_1=\rho(b_0-a_0)=\rho\lambda
a1′−a0=b0−b1′=ρ(b0−a0)=ρλ
其中,
ρ
<
1
2
\rho<\frac{1}{2}
ρ<21。比较
f
(
a
1
′
)
f(a'_1)
f(a1′)与
f
(
b
1
′
)
f(b'_1)
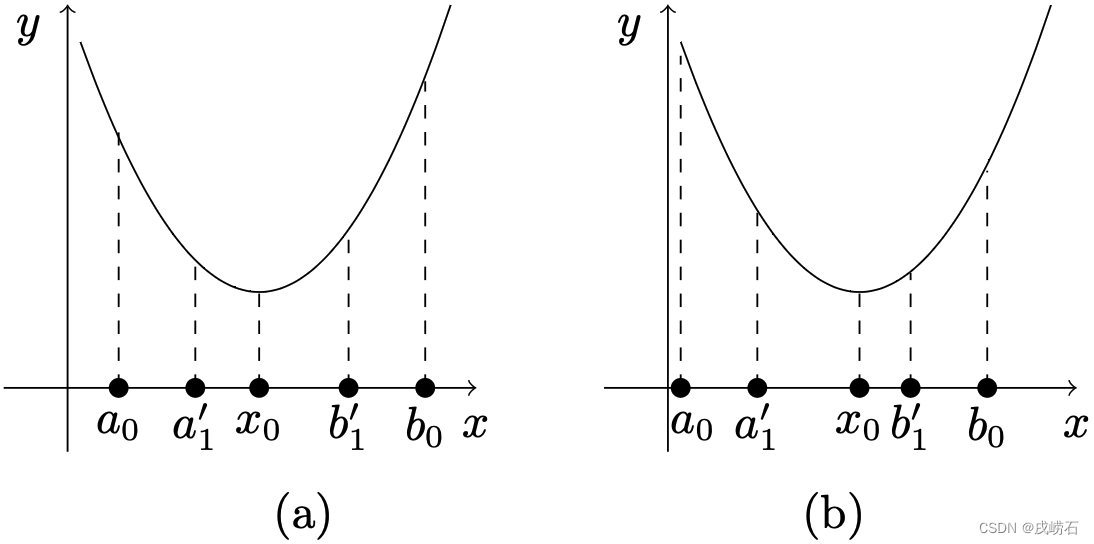
f(b1′),若
f
(
a
1
′
)
<
f
(
b
1
′
)
f(a'_1)<f(b'_1)
f(a1′)<f(b1′),则
x
0
∈
[
a
0
,
b
1
′
]
x_0\in[a_0,b'_1]
x0∈[a0,b1′](见下图(a))。否则,即
f
(
b
1
′
)
≤
f
(
a
1
′
)
)
f(b'_1)\leq f(a'_1))
f(b1′)≤f(a1′)),则
x
0
∈
[
a
1
′
,
b
0
]
x_0\in[a'_1,b_0]
x0∈[a1′,b0](见下图(b)))。对于前者,令
[
a
1
,
b
1
]
=
[
a
0
,
b
1
′
]
[a_1,b_1]=[a_0,b'_1]
[a1,b1]=[a0,b1′]。相仿地,对后者令
[
a
1
,
b
1
]
=
[
a
1
′
,
b
0
]
[a_1,b_1]=[a'_1,b_0]
[a1,b1]=[a1′,b0]。无论那种情形,变换后的区间
[
a
1
,
b
1
]
[a_1,b_1]
[a1,b1]其长度缩短为
λ
(
1
−
ρ
)
\lambda(1-\rho)
λ(1−ρ),且
x
0
∈
[
a
1
,
b
1
]
x_0\in[a_1,b_1]
x0∈[a1,b1]。继续用上述方法,在
[
a
1
,
a
2
]
[a_1,a_2]
[a1,a2]中插入备选点
a
2
′
a'_2
a2′和
b
2
′
b'_2
b2′,可得长度为
λ
(
1
−
ρ
)
2
\lambda(1-\rho)^2
λ(1−ρ)2且包含
x
0
x_0
x0的压缩区间
[
a
2
,
b
2
]
[a_2,b_2]
[a2,b2]。按此方式迭代
k
k
k次,得到的含有
x
0
x_0
x0的压缩区间
[
a
k
,
b
k
]
[a_k,b_k]
[ak,bk]长度为
λ
(
1
−
ρ
)
k
\lambda(1-\rho)^k
λ(1−ρ)k。对给定的容错误差
ε
>
0
\varepsilon>0
ε>0,若
(
1
−
ρ
)
k
λ
<
ε
(1-\rho)^k\lambda<\varepsilon
(1−ρ)kλ<ε,则停止迭代,当前区间
[
a
k
,
b
k
]
[a_k,b_k]
[ak,bk]内任一点均可充当最优解
x
0
x_0
x0的近似值。否则继续进行相同的迭代计算,直至满足精度要求。
事实上,我们在第一次迭代确定区间
[
a
1
,
b
1
]
[a_1,b_1]
[a1,b1]时,有一个备选点
a
1
′
∈
[
a
1
,
b
1
]
a'_1\in[a_1,b_1]
a1′∈[a1,b1](
=
[
a
0
,
b
1
′
]
=[a_0,b'_1]
=[a0,b1′]见上图(a)所示情形)或
b
1
′
∈
[
a
1
,
b
1
]
b'_1\in[a_1,b_1]
b1′∈[a1,b1](
=
[
a
1
′
,
b
0
]
=[a'_1,b_0]
=[a1′,b0]上图(b)),在该点处的函数值已计算过。我们可以利用这个点,作为第二次迭代时要插入的备选点
b
2
′
b'_2
b2′(或
a
2
′
a'_2
a2′)。这样可以减少一次函数值
f
(
b
2
′
)
f(b'_2)
f(b2′)(或
f
(
a
2
′
)
f(a'_2)
f(a2′))的计算。以上图(a)情形为例,在第一次迭代中所取的点
a
1
,
b
1
a_1,b_1
a1,b1为
a
0
,
b
1
′
a_0,b'_1
a0,b1′,第二次迭代时,以
a
1
′
a'_1
a1′作为
b
2
′
b'_2
b2′。若选择
ρ
=
3
−
5
2
≈
0.382
\rho=\frac{3-\sqrt{5}}{2}\approx0.382
ρ=23−5≈0.382,即可使得
[
b
2
′
,
b
1
′
]
[b'_2,b'_1]
[b2′,b1′]的长度为
ρ
(
1
−
ρ
)
λ
\rho(1-\rho)\lambda
ρ(1−ρ)λ,如下图所示(为使表达简洁,图中假定
λ
=
1
\lambda=1
λ=1)。由于每次迭代,区间长度的压缩系数为黄金分割数
1
−
ρ
=
5
−
1
2
≈
0.618
1-\rho=\frac{\sqrt{5}-1}{2}\approx0.618
1−ρ=25−1≈0.618,算法由此得名。

Python用于科学计算的工具包scipy中,有一个optimize模块,提供大量用于最优化问题解决方案。其中有一个用于计算指定一元函数
f
(
x
)
f(x)
f(x)局部最优解的函数minimize_scalar。该函数常用的接口为
minimize_
scalar(fun, bracket, method)
\text{minimize\_{}scalar(fun, bracket, method)}
minimize_scalar(fun, bracket, method)
其中,参数fun表示目标函数
f
(
x
)
f(x)
f(x),bracket表示
f
(
x
)
f(x)
f(x)的单峰区间信息,method表示所要采用的搜索算法。我们只要将表示目标函数、单峰区间(可用myBracket函数计算,详见博文《连续函数的单峰区间计算》)及实现搜索算法的函数传递给minimize_scalar的参数fun、bracket和method即可望算得目标函数的局部最优解。用户自定义搜索算法函数需符合下列的接口规范
custmin(fun, bracket, args=(), ..., **options)
\text{custmin(fun, bracket, args=(), ..., **options)}
custmin(fun, bracket, args=(), ..., **options)
其中函数名custmin可任取,形式参数表fun, bracket, args=(), …中命名参数(如此处的args及其后续的参数)需排列在任意参数(此处的fun,bracket)之后。特殊的options参数是minimize_scalar在调用时向本函数传递所需的自定义实际参数的机制。
下列代码实现黄金分割搜索算法。
from scipy.optimize import OptimizeResult
def myGolden(fun,bracket,gtol=1e-6,**options):
a0,b0=bracket #初始化区间[a0,b0]
rho=0.382 #ρ=1-0.618
lam=b0-a0 #区间长度λ
a1,b1=a0+lam*rho,b0-lam*rho #首次插入点
f1,f2=fun(a1),fun(b1) #区间端点函数值
k=1 #迭代次数
while lam>gtol: #重复迭代
if f1<f2: #情形(a)
t,b0,f2=0,b1,f1 #保留左端点,更新右端点
else: #情形(b)
t,a0,f1=1,a1,f2 #保留右端点,更新左端点
lam=lam*(1-rho) #更新区间长度
k+=1 #迭代次数自增1
if t==0: #情形(a)
b1=a1 #插入点b1更新为a1
a1=a0+lam*rho #更新插入点a1
f1=fun(a1) #计算a1处函数值
else: #情形(b)
a1=b1 #插入点a1更新为b1
b1=b0-lam*rho #更新插入点b1
f2=fun(b1) #计算b1处函数值
bestx=(a0+b0)/2 #计算最优解近似值
besty=fun(bestx) #计算最优值近似值
return OptimizeResult(fun=besty, x=bestx, nit=k)
程序的第2~26行定义实现黄金分割算法的Python函数myGolden。参数fun表示目标函数
f
(
x
)
f(x)
f(x),参数bracket表示单峰区间
[
a
0
,
b
0
]
[a_0,b_0]
[a0,b0],gtol表示容错误差
ε
\varepsilon
ε,缺省值为
1
0
−
6
10^{-6}
10−6。minimize_scalar可利用参数**options将自命名参数gtol的具体值传递给由method接收的myGolden。
第3~8行执行初始化操作:第3行从参数bracket读取函数
f
(
x
)
f(x)
f(x)的单峰区间端点
(
a
0
,
b
0
)
(a_0,b_0)
(a0,b0)赋予a0,b0。第4行设置缩放系数
ρ
=
0.382
\rho=0.382
ρ=0.382赋予rho。第5行将区间长度
λ
\lambda
λ初始化为
b
0
−
a
0
b_0-a_0
b0−a0赋予lam。第6行用区间端点处的函数值
f
(
a
0
)
,
f
(
b
0
)
f(a_0),f(b_0)
f(a0),f(b0)初始化f1,f2。第8行将迭代次数k初始化为1。
第9~23行的while循环执行迭代操作:第10~13行的if-else分支根据条件
f
(
a
k
)
<
f
(
b
k
)
f(a_k)<f(b_k)
f(ak)<f(bk)
是否成立,是否成立,确定是前图中所示情形(a)还是(b)。若为前者置标志t为0,保留左端点a0(仅将右端点b0更新为插入点b1),并更新右端点处的函数值f2。否则置t为1,保留右端点b0(将左端点a0更新为插入点a1),更新左端点处的函数值f1。第14行计算新的压缩区间
[
a
0
,
b
0
]
[a_0,b_0]
[a0,b0]的长度
λ
\lambda
λ,第15行将迭代次数
k
k
k自增1。第16~23行的if-else分支根据表示不同情形的t值(0或1),确定新的插入点的计算a1、b1的计算,并计算需更新的插入点处的函数值。
当压缩区间
[
a
0
,
b
0
]
[a_0,b_0]
[a0,b0]的长度
λ
\lambda
λ小于容错误差
ε
\varepsilon
ε时,迭代完成。第24行取
[
a
0
,
b
0
]
[a_0,b_0]
[a0,b0]的中点作为最优解
x
0
x_0
x0的近似值,赋予bestx。第25行计算目标函数在最优解处的近似值,赋予besty。第26行返回值为
OptimizeResult(fun=besty, x=bestx, nit=k)
\text{OptimizeResult(fun=besty, x=bestx, nit=k)}
OptimizeResult(fun=besty, x=bestx, nit=k)
是用前面算得的最优解
x
0
x_0
x0的近似值bestx,最优解处的函数值
f
(
x
0
)
f(x_0)
f(x0)的近似值besty以及迭代次数k创建的OptimizeResult类(第1行导入)对象。
例1 用myGolden方法计算函数
f
(
x
)
=
x
4
−
14
x
3
+
60
x
2
−
70
x
f(x)=x^4-14x^3+60x^2-70x
f(x)=x4−14x3+60x2−70x在
x
=
0
x=0
x=0近旁的局部最优解。
解:下列代码计算本例
from scipy.optimize import minimize_scalar #导入minimize_scalar
f=lambda x:x**4-14*x**3+60*x**2-70*x #设置目标函数
bracket=myBracket(f,0) #计算单峰区间
res=minimize_scalar(f,bracket,method=myGolden,options={'gtol':1.48e-8}) #计算最优解
print(res)
程序的第2行定义目标函数 f ( x ) f(x) f(x),第3行调用myBracket函数(详见博文《连续函数的单峰区间计算》)计算 f ( x ) f(x) f(x)在 x = 0 x=0 x=0附近的单峰区间 [ a 0 , b 0 ] [a_0,b_0] [a0,b0]赋予bracket。第4行调用minimize_scalar,传递 f ( x ) f(x) f(x)给参数fun,传递 [ a 0 , b 0 ] [a_0,b_0] [a0,b0]给bracket,传递myGolden给参数method,传递字典型数据{‘gtol’:1.48e-8}给参数options,籍此向myGolden传递容错误差 ε = 1.48 \varepsilon=1.48 ε=1.48✕ 1 0 − 8 10^{-8} 10−8。运行程序,输出
fun: -24.369601567349775
nit: 38
x: 0.7808836405154187
意味着myGolden以容错误差
ε
=
1.48
×
1
0
−
8
\varepsilon=1.48\times10^{-8}
ε=1.48×10−8,迭代38次,算得最优解近似值为0.7808836405154187,最优解处函数近似值-24.369601567349775。
Scipy.optimization模块为minimize_scalar提供了三个常用的搜索算法:
brent
bounded
golden
\begin{array}{l} \text{brent}\\ \text{bounded}\\ \text{golden} \end{array}
brentboundedgolden
供程序员选择使用,其中的golden方法就是实现的黄金分割算法。
例2 用Python提供的golden方法计算例1中函数
f
(
x
)
=
x
4
−
14
x
3
+
60
x
2
−
70
x
f(x)=x^4-14x^3+60x^2-70x
f(x)=x4−14x3+60x2−70x在
x
=
0
x=0
x=0近旁的局部最优解。
解:下列代码计算本例
from scipy.optimize import minimize_scalar #导入minimize_scalar
f=lambda x:x**4-14*x**3+60*x**2-70*x #设置目标函数
bracket=myBracket(f,0) #计算x=0近旁的单峰区间
res=minimize_scalar(f,bracket,method='golden') #计算最优解
print(res)
注意第4行调用minimize_scalar时传递给method的参数为’golden’(要打引号),表示系统提供的golden方法。运行程序,输出
fun: -24.369601567355033
message: '\nOptimization terminated successfully;\nThe returned valuesatisfies the termination criteria\n(using xtol = 1.4901161193847656e-08 )'
nfev: 44
nit: 39
success: True
x: 0.7808840597145699
与例1的输出比较,我们的自己的myGolden无论是计算精度还是计算效率并不输给系统提供的golden。
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!






















 1079
1079











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








