POJ - Fibonacci 【快速幂 + 矩阵】-CSDN博客

本文链接：https://blog.csdn.net/miskeen/article/details/20067945

Description

In the Fibonacci integer sequence, F₀ = 0, F₁ = 1, and F_n = F_n_{− 1} + F_n_{− 2} for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

Given an integer n, your goal is to compute the last 4 digits of F_n.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of F_n. If the last four digits of F_n are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print F_n mod 10000).

Sample Input

Sample Output

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

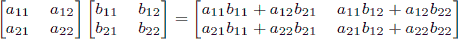Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

⑴ 关于这题的主要思路是快速幂与矩阵的结合，首先，将这个问题转化为矩阵问题。参考下面的等式：

$\begin{equation*} \begin{split} \begin{bmatrix} F_{n-1} & F_{n-2}\\ F_{n-2} & F_{n-3} \end{bmatrix} \cdot \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix} &= \begin{bmatrix} F_{n-1}+F_{n-2} & F_{n-2}+F_{n-3}\\ F_{n-2}+F_{n-3} & F_{n-2} \end{bmatrix}\\ &= \begin{bmatrix} F_{n} & F_{n-1}\\ F_{n-1} & F_{n-2} \end{bmatrix}\\ \end{split} \end{equation*}$

$\begin{bmatrix} F_{n+1} & F_{n}\\ F_{n} & F_{n-1} \end{bmatrix}= \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^{n}$ 这样，求 $F_n$ 就变成了 $\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^{n}$ ，接下来就是用快速幂的方法解决这个问题。

⑵关于快速幂，这里还是详细的分析一下咯！

#include <iostream>

using namespace std;
/*
    假设a = 2 b = 11, 那么，a^b = 2^11,分析结果如下：
    ①  b(10) ---> b(2)  1 0 1 1
    ②  a^b = 2^11 ---> 2^(2^3*1 + 2^2*0 + 2^1*1 + 2^0*1)
    ③  a^b = 2^11 ---> 2^(2^3)*2^(2^1)*2^(2^0)
*/
int pow(int n,int m)   // 快速幂
{
	int res = 1,s = n;
	while(m)
	{
		if(m&1)
		res *= s;
		s *= s;
		m >>= 1;
	}
	return res;
}
int main()
{
	int a,b;
	cin >> a >> b;
	cout << pow(a,b) << endl;
	return 0;
}

⑶通过上面的步骤，将快速幂与矩阵结合，这个问题就解决了。时间复杂度O(logn)，下面是具体的实现的代码：

#include <iostream>

using namespace std;
const int mod = 10000;
class Matrix
{
public:
	Matrix();
	int map[2][2];
	Matrix operator *(const Matrix &t);
	Matrix& operator =(const Matrix &t);
};

Matrix::Matrix()
{
	map[0][0] = 1;
	map[0][1] = 1;
	map[1][0] = 1;
	map[1][1] = 0;
}
Matrix Matrix::operator *(const Matrix &t)
{
	Matrix ans;
	ans.map[0][0] = (map[0][0]*t.map[0][0]+map[0][1]*t.map[1][0]) % mod;
	ans.map[0][1] = (map[0][0]*t.map[0][1]+map[0][1]*t.map[1][1]) % mod;
	ans.map[1][0] = (map[1][0]*t.map[0][0]+map[1][1]*t.map[1][0]) % mod;
	ans.map[1][1] = (map[1][0]*t.map[0][1]+map[1][1]*t.map[1][1]) % mod;
	return ans;
}
Matrix& Matrix::operator =(const Matrix &t)
{
	for(int i = 0; i <= 1; ++i)
	{
		for(int j = 0; j <= 1; ++j)
		{
			map[i][j] = t.map[i][j];
		}
	}
	return *this;
}
int main(int argc, char const *argv[])
{
	int n;
	while(cin >> n,~n)
	{
		Matrix res,k;
		while(n)
		{
			if(n&1) res = res * k;
			k = k * k;
			n >>= 1;
		}
		cout << res.map[1][1] << endl;
	}
	return 0;
}