【论文概述】analysis of alpha-beta pruning

这篇论文出自Donald E. Knuth and Ronald W. Moore之手，原文，是北京大学本科生算法设计与分析2014年春季课程的限选论文之一。以下是其梗概，也算是掺杂入一点个人理解得压缩翻译吧~毕竟原文34页实在太长，我在word里写完的梗概只有4页，并且其中还有一页多的图表与代码。

这篇论文主要说了alpha-beta pruning的设计思路以及对其复杂度进行了大量的分析。

    首先，我们先将two-person games严谨地定义与表述一下。这个过程是从一个初始position开始，双方轮流按照规则对position进行操作使其变为另一个position，直到一方获胜为止。

    公设要求对每个position下都只能依规则进行有限种操作，由此可以证明存在函数N(p)=从p开始导出的所有position所拥有的操作数的最大值。

    对于没有进一步合法操作的position，定义对于面对这个position的玩家，其value:=f(p)。对另一个玩家而言，value=-f(p)。

   对于所有的position,我们定义其value:=F(p)为从这个position开始，在另一个玩家也采取最优策略的情况下，这个玩家所能够抵达的一个无法进一步操作的position的value（当然是对于面对这个position的玩家）。我们有：F(p)=max(-F(p₁), -F(p₂)….. -F(p_d))（d=0时F(p)= f(p)）上述的决策过程即为negmax模型。等价地，我们还有minimax模型。这两个模型本质上等价，但出于表述上的差异，在实际上说明问题的时候各有用处。

    上述模型的缺陷在于太过保守，是假设对手无所不能的情况下的保守策略，这在实战中会很明显。

negmax模型的伪代码：
integer procedmre F (position p):
    begin integer m, i, t, d;
        determine the successor positions P1 , - . . , Pd;
        if d = 0 then F := f(p) else
        begin m := - ∞;
            for i := 1 step 1 until d do
            begin. t :=-F(Pi)
                if t > m then m := t;
            end;
        F := m;
    end;
end.

    上述算法是正确的，但是是蛮力的，可以通过增加α与β两个限制界对其进行剪枝。我们在分析之前先看一下引入两个剪枝量之后的伪代码：

integer procedure F2 (position p, integer alpha, integer beta):
    begin integer m, i, t, d;
        determine the successor positions p1, ..., Pd;
        if d = 0 then F2 := f(p) else
        begin m := alpha;
            for i := 1 step 1 until d do
            begin t : = - F2(pi, -beta, -m);
                if t > m then m := t;
                if m ≥ beta then go to done;
        end;
    done: F2 : = m;
    end;
end;

    （F2(p,-∞, ∞)为输入获取F(p)的初始值）我们保证输出的F(p)的值处在alpha~beta之间。alpha的值，代表了同层已搜索的position的最大估值（表明我这里已经有一种做法可以实现了无论对方怎么走我都至少收获alpha的收益，小于这个收益值的就可以被无视了），beta的值表示上一层对方的最大估值的相反数（表明对方之前已经有一种走法使得我的收益达到beta了，我只需要知道我这一个position有一种决策可以使得我方的收益大于beta就行了，因为知道了这一点对方的决策就不会让我有机会进行这个position的决策的进行）。

 

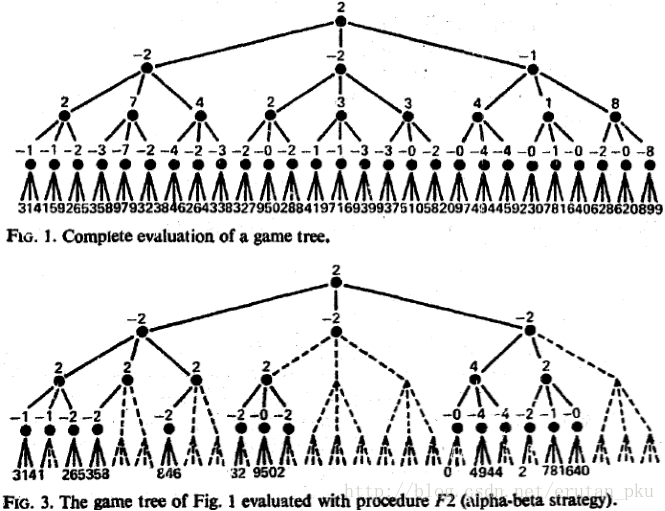
    下面一组图描绘了alpha-beta剪枝的效果：

    文中在这里还描绘了应用minimax模型的alpha-beta剪枝的伪代码，在此我就略过了。在alpha-beta剪枝的实现中，还有一些细节，比如p1~pd的确定（有一个单独的函数并生成链表）以及可以使用非递归的方式进行搜索（使用栈的方法，在栈中储存alpha,beta的值什么地使用了一些技巧）。

    在实际应用中，由于搜索空间实在太大，我们可以限制搜索深度（而不是搜索到底）。在大多数情况下，只要判断能不能走的规则不要太复杂，主要的时间都花费在对末端position的估价上。还有人采用一种可能性估价的函数来进行变深搜索，对于很不可能走到的点给予很低的可能性，对于很可能或者必须走的点给予很高的可能性。在终止条件中不对宽度进行判断而对于复合可能性进行判断，从而将更多的精力放在更可能的情况上。并且如果我们最开始就对于结果有一个预期，不用F2(p,-∞, ∞)而是F2(p,a,b)作为初始的剪枝条件，也会大大提高我们的搜索效率（但是这样会有一些风险，上面图中如果选用F2(p,-9,9)的话风险是没有，但是效果也没有）。

 

   【接下来的两段是对alpha-beta剪枝算法复杂度上下界的计算与证明，简直数学到爆。】

   首先，为了更好地表示一棵游戏树中的节点，我们对其进行序列坐标标注。根节点用空序列进行标注，对某一节点P，若其标注序列为S=p1p2…pm，则其d个子节点的标注序列为p1p2…pm1,p1p2…pm2,…,p1p2…pmd.

    我们称一个节点是critical的，当其坐标中所有奇数位或所有偶数位均为1.

   定理一：若一个估值有限游戏树，且每一个节点的第一子节点都是最优的，则用alpha-beta剪枝对其搜索的搜索空间就是这棵树的所有critical 节点。（第一子节点最优即若S非终结，则F(S)=-F(S1)）（归纳地证明，不是那么显然）

    推论一：对于一个深度为l的满足定理1条件的游戏树，存在常数d，使得其alpha-beta搜索到的终结节点的数目为d^floor(l/2)+ d^ceil(l/2)-1.（比较显然。）

    推论二（更一般地）：这样的表述一棵随机的游戏树：第j层的节点不是终点的概率为pj，平均有dj个子节点，于是在定理一的假设加，第l层节点被我们搜索到的有：(d0q1d2q3…dl-2ql-1)+(q0d1q2d3…ql-2dl-1)-(q0q1…ql-1),l是偶数的情况（奇数类似，易证）。

（原文下一段中提到这个表述的精确化表述，不过意义不大）（当qj=1，dj=d的时候，推论二退化为推论1）

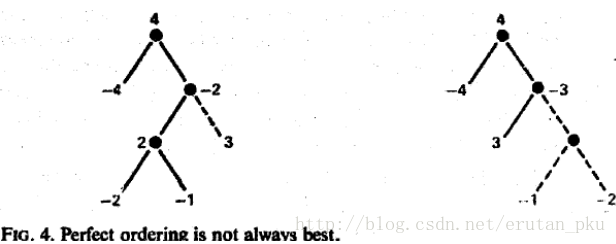
    直觉上，定理一的假设条件是我们alpha-beta剪枝的最优情况。但是下图给出了一个反例，使得我们追求的真理更加扑朔迷离。【不过下面这个图让我看得扑朔迷离，没理解这怎么就是反例了…左右两边完全不是一样的树呀…】

    定理二：对"游戏树和"搜索算法，存在这课树的一个重排列（可修改子节点标号），对这个重排列的alpha-beta剪枝搜索到的终端节点在该搜索算法中均被搜索到。特别地，如果根节点的结果是有限值的话，alpha-beta剪枝搜索到的终端点就是所有的critical节点。（我们假设每一个终端的估值之间没有相关性，或者即使有我们的算法也不知道）

【我不保证这个定理我理解得正确，下面的证明看起来不那么容易…我没有看】

    推论三： 任何一个处理uniform game tree的算法至少需要处理d^floor(h/2)+d^ceil(h/2)-1个终端节点。alpha-beta剪枝在某些节点满足定理一中的最优性原则的时候可以去到这个下界。【所谓的uniform game tree是指h层，除了第h层全为终结节点之外其余每个节点都有d个子节点的游戏树。第二句话中的“某些节点”在原文中有比较复杂而明确的表述。】

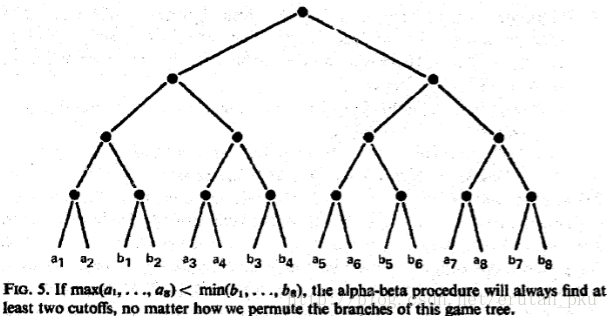
       接下来我们考虑最坏情况。显然，对于任意有限游戏树，我们都有一种最终节点的标价方式，使得我们的alpha-beta剪枝需要搜索所有的终结节点才能够得出最终结果。但也有树和固定的终结节点标价，使得我们仅仅对这个树进行重排列并不能alpha-beta剪枝完全丧失作用，比如下图：

    但是上面讨论的这几种最坏情况实在是不太可能出现，我们主要用随机情况来研究这个算法的上界。不过由于太过复杂，这实在是搞不定。所以说我们退而求其次地去研究比F2要稍微差一点但会简单不少的F1算法（这个算法是没有deep cutoffs，前面我为了省事，将其略去了，可以去原文中看一下。）我们的研究对象依然是uniform game tree.（不妨每个终点的估值都是互异的）

    我们记一个参数为h和d的uniform game tree在F1算法中需要检测的终端节点数为T(d,h)。我们经过好几页值的复杂的计算与推导之后，我们有如下定理：（下面几个定理谈的都是期望。）

   定理3：T(d,2)=∑(1≤i,j≤d)pij，其中pij=1/((i-1+(j-1)/d)C(i-1))，也就是说T(d,2)=Q(d^2/log(d)).

   定理4：T(d,h)=O((r(d) ) ^ h)，其中r(d)是d*d的矩阵|sqrt(pij)|的最大特征值

   定理5：lim(hà∞)T(d,h) ^ 1/h = Q(d/log(d)).

   【上面这些分析过程是非常数学与复杂的，我从其中摘出了结论跳过了过程，很可能会有些理解得不到位的地方。】

   我们这个分析的模型做了如下假设：未考虑F2相对于F1所增加的深度裁剪，随机化了子节点序列，终端估价默认互异并且相互独立。这每一条假设都使得我们的求出来的这个界比实际的上界要稍微大上那么一点点。我们会稍微地看看具体大了多点….比如说如果使用了F2的话，上面推出那些定理的复杂分析中的有一个量中有一个会被计算n+2次方的地方从sqrt(d)变成了sqrt(d-3/4)+1/2。【我觉得具体是怎么回事并不太重要，只是感受一下就好了】

    接下来我们考虑一下终结节点估价相关的情况。（这种情况在实际中是非常常见的）文中提出了一个total dependency model：对于pi的所有终端子节点与pj的所有终端子节点，要么pi的都更大一些，要么pj的都更大一些。这个模型等价于对每个节点的d个子节点进行0~d-1的标号，然后每个节点的估价等于其父节点的估价乘以d在加上自己的估价。（上一句话的估价在非终结节点处不等同与该节点的估价F(p)，这个模型在uniform game tree中表现得更加明晰，有兴趣可以看原文图8。还可以引入进位制的观点来看这个模型）

    经过一系列计算，我们如下定理（还是关于期望的讨论）：

    定理6：对于参数为d和h的random totally dependentuniform game tree,应用alpha-beta剪枝所搜索的终端节点的期望为((d-Hd)/(d-Hd^2))*(d^ceil(h/2)+ Hd*d^floor(h/2)-hd^(h+1)-hd^h)+hd(h)，其中Hd=1+1/2+…+1/d

    推论4：d≥3时，这个值是推论3中值的f(d)倍（f(d)表示一个只和d有关的量）

有所疏漏，在所难免。忘诸大神指教...O(∩_∩)O谢谢~