线索二叉树

目录

线索二叉树概念

遍历二叉树就是以一定规则将二叉树中的节点排列成一个线性序列，从而得到二叉树节点的各种遍历序列。其实质就是对一个非线性序列进行线性化操作，使得在这个访问序列中每一个节点（除第一个和最后一个）都有一个直接前驱和直接后继。

传统链式存储能体现父子关系，不能直接得到节点在遍历中的前驱和后继。通过观察，我们发现在二叉树表示的二叉树中存在大量的空指针，若利用这些空链域指向其直接前驱或直接后继的指针，则可以更方便地运用某些二叉树操作算法。引入线索二叉树就是为了加快查找节点前驱和后继的速度。

typedef struct ThreadNode{
    ElemType data;
    struct ThreadNode *lchild, *rchild;
    int ltag, rtag;
} ThreadNode, *ThreadTree;
//其中
//ltag = 0 表示lchild指示节点的左孩子
//ltag = 1 表示lchild指示节点的前驱
//rtag同理

以这种节点结构构成的二叉链表作为二叉树的存储结构，叫做线索链表，其中指向节点前驱或后继的指针，叫做线索。加上线索的二叉树称为线索二叉树。对二叉树以某种次序遍历使其变成线索二叉树的工程叫做线索化。

线索二叉树的构造

对二叉树的线索化，实质就是遍历一次二叉树，在遍历过程中，检查当前节点左右节点是否为空，若为空，将他们指向前驱节点或后继节点的线索。

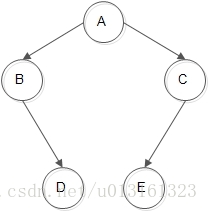
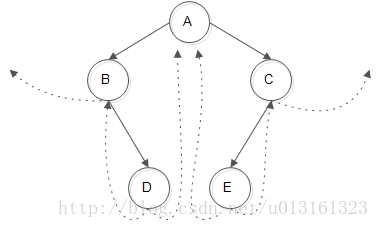
以次二叉树为例，通过中序遍历时对二叉树线索化，而我们可以直观地知道此二叉树的中序遍历序列是：B-D-A-E-C。其线索化的链接情况是：

以D为例，作为说明：在中序中，D在遍历序列中的前驱是B，而A是后继，所以D原本两个为NULL的指针分别指向了它的前驱B和后继A。

其中序遍历对二叉树线索化的递归算法如下：

void InThread(ThreadTree &p, ThreadTree &pre) {
    if (p != NULL) {
        InTHread(p->lchild, pre);
        if (p->lchild == NULL) {
            p->lchild = pre;
            p->ltag = 1;
        }
        if (pre != NULL && pre->rchild == NULL) {
            pre->rchild = p;
            pre->rtag = 1;
        }
        pre = p;
        InThread(p->rchild, pre);
    }
}

通过中序遍历建立中序线索二叉树的主过程算法如下：

void CreateInTHread(ThreadTree T) {
    ThreadTree pre = NULL;
    if (T != NULL) {
        InThread(T, pre);
        pre->rchild = NULL;
        pre->rtag = 1;
    }
}

线索二叉树的遍历

中序线索化二叉树主要是为访问运算服务的，这种遍历不在需要借助栈，因为它的节点中隐含了线索二叉树的前驱和后继信息。利用线索二叉树，可以实现二叉树遍历的非递归算法。不含头结点的线索二叉树的遍历算法如下（含头结点的相当于建立一个双向线索链表，感兴趣的话可以自行搜索一下）：

1.求中序线索二叉树中中序序列下第一个节点：

ThreadNode *FirstNode(ThreadNode *p) {
    while (p->ltag == 0) p=p->lchild;
    return p;
}

2.求中序线索二叉树中节点p在中序序列下的后继节点：

ThreadNode *NextNode(ThreadNode *p) {
    if (p->rtag == 0) return FirstNode(p->rchild);
    else return p->rchild;
}

3.利用以上两个算法，可以写出不含头结点的中序遍历的算法：

void Inorder(ThreadNode *T) {
    for (ThreadNode *p=FirstNode(T); p!=NULL; p=NextNode(p))
        visit(p);
}