01背包优化平民理解思路

最近准备找工作了，研究了一下动态规划的问题，发现开始的状态方程还是好理解的

有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。

普通状态转移方程：

f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]} ，但是当我们将空间复杂度优化的时候，就会出现理解上的难点，不理解，特地我将二维数组与一维数组的代码都粘贴上来

二维的（未优化的）

int f[V][N] = {0};
	int v, n, ci, wi;
	cin >> v >> n;
	for (int i = 1;i <= n;i++)
	{
		cin >> ci >> wi;
		for (int j = v; j >= 0; j--) 
		{
			if (j >= ci)
				f[j][i] = max(f[j - ci][i - 1] + wi, f[j][i - 1]);
			else
				f[j][i] = f[j][i - 1];
		}
	}

那么，如果只用一个数组f[0..V]，能不能保证第i次循环结束后f[v]中表示的就是我们定义的状态f[i][v]呢？f[i][v]是由f[i-1][v]和f[i-1][v-c[i]]两个子问题递推而来，能否保证在推f[i][v]时（也即在第i次主循环中推f[v]时）能够得到f[i-1][v]和f[i-1][v-c[i]]的值呢？

我们观察到上图的代码很简单，选出二维数组的每一个对应的值，那么就可以找到f[j][i]的最大值，这样就得到价值最大的了，但是优化成一维的话，怎么理解呢，我先粘贴一下一维的代码：

int times, n, v, ci, wi;
	int f[maxV] = { 0 };
	cin >> v >> n;
	for (int i = 0; i < n; i++) {
		cin >> ci >> wi;
		for (int j = v; j >= 0; j--) {
			if (j >= ci)
				f[j] = max(f[j - ci] + wi, f[j]);
		}
		for (int i = v; i >= 0; i--) cout << f[i] << " ";
		cout << endl;
	}	

可以看出 由于V是从V到0的，也就是说，除了初始化的部分，我们最先更新的是V的值，也就是从后往前更新的，恰巧，我们的一维状态方程是 f[v]=max{f[v],f[v-c[i]]+w[i]};这就要求我们在求方程的左边部门的时候（i）右边对应的i是i-1的f函数的值，这样才能优化成一维，而我们是从后往前更新的，那么f[v]存储的值不就是i-1的值吗，试想一下，有f[0],f[1],f[2],f[3]下标都是i-1.当我们更新i的时候，拿f[3]举例，f[3] (下标)= f[3-ci]（下标i-1） +f[3]（下标i-1）,上面的代码逻辑正符合此逻辑，这样我们就可以节省到很大的空间，说白了，这个原理就是重复利用空间，而二维数组是没有重复利用的，当j>ci的时候，二维跟一维一样，要求值，当不大于的时候，二维要存入之前的值，而一维恰恰省了，因为现在它存的本身就是之前的值:我再配合测试数据来解释一下，使大家能更轻易的理解：

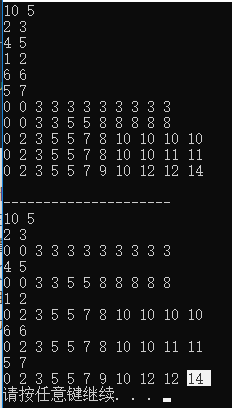
上边是二维的数组输出的值，下边是一维的每一层输出的值，可以看到效果是一样的，区别就是一维的重复利用空间，空间每次更新都是从后向前更新，因为后边的更新要依赖于前边的i-1的状态值。这样就达到目的了.