Minimum Moves to Move a Box to Their Target Location

A storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.

The game is represented by an m x n grid of characters grid where each element is a wall, floor, or box.

Your task is to move the box 'B' to the target position 'T' under the following rules:

• The character 'S' represents the player. The player can move up, down, left, right in grid if it is a floor (empty cell).
• The character '.' represents the floor which means a free cell to walk.
• The character '#' represents the wall which means an obstacle (impossible to walk there).
• There is only one box 'B' and one target cell 'T' in the grid.
• The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a push.
• The player cannot walk through the box.

Return the minimum number of pushes to move the box to the target. If there is no way to reach the target, return -1.

Example 1:

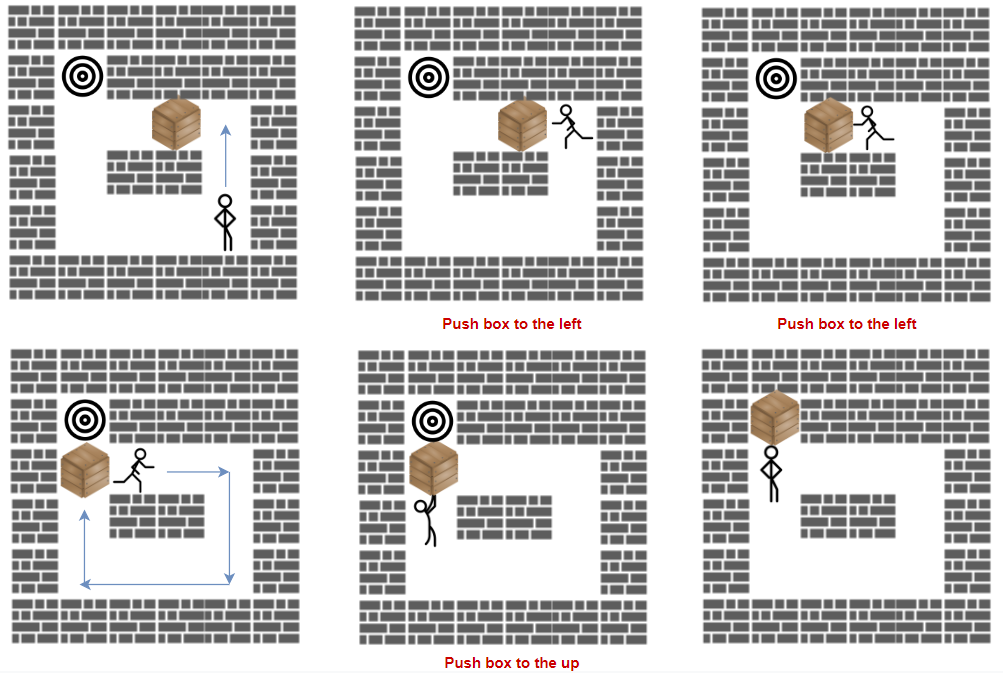
Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#",".","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 3
Explanation: We return only the number of times the box is pushed.

思路：这题是leetcode唯一一个用arrayDeque写BFS的，因为人的移动并不是下一层，还是属于当前层，所以需要insert到前面，箱子push了才会是下一层，加到queue的后面，也就是要保证整个queue是层级递增的，这样才能保证最后遇见终点的时候，step是最小的，这样BFS才能有效果，那么状态的记录就是四个状态, bx, by, px, py; 分两种情况，一种是人走，不影响层级，丢到queue前面，step不递增：memo[bx][by][npx][npy] = memo[bx][by][px][py];，另外一种是箱子移动，首先人要在箱子的四周， if(Math.abs(px - bx) + Math.abs(py - by) == 1)，然后人移动到箱子的方向dir就是箱子的移动方向。同时step递增一步：memo[nbx][nby][bx][by] = memo[bx][by][px][py] + 1;

class Solution {
    class Node {
        public int px;
        public int py;
        public int bx;
        public int by;
        public Node(int bx, int by, int px, int py) {
            this.px = px;
            this.py = py;
            this.bx = bx;
            this.by = by;
        }
    }
    
    public int minPushBox(char[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        
        int bx = -1, by = -1, px = -1, py = -1, tx = -1, ty = -1;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(grid[i][j] == 'B') {
                    bx = i;
                    by = j;
                    grid[i][j] = '.';
                } else if(grid[i][j] == 'S') {
                    px = i;
                    py = j;
                    grid[i][j] = '.';
                } else if(grid[i][j] == 'T') {
                    tx = i;
                    ty = j;
                    grid[i][j] = '.';
                }
            }
        }
        
        int[][][][] dp = new int[21][21][21][21];
        for(int i = 0; i < 21; i++) {
            for(int j = 0; j < 21; j++) {
                for(int k = 0; k < 21; k++) {
                    Arrays.fill(dp[i][j][k], -1);
                }
            }
        }
        dp[bx][by][px][py] = 0;
        
        ArrayDeque<Node> arrayDeque = new ArrayDeque<Node>();
        arrayDeque.offer(new Node(bx, by, px, py));
        
        int[][] dirs = new int[][]{{0,1},{0,-1},{-1,0},{1,0}};
        while(!arrayDeque.isEmpty()) {
            Node node = arrayDeque.poll();
            bx = node.bx;
            by = node.by;
            px = node.px;
            py = node.py;
            
            if(bx == tx && by == ty) {
                return dp[bx][by][px][py];
            }
            
            // move person add front;
            for(int[] dir: dirs) {
                int npx = px + dir[0];
                int npy = py + dir[1];
                if(0 <= npx && npx < m && 0 <= npy && npy < n && grid[npx][npy] == '.'
                  && !(npx == bx && npy == by) && dp[bx][by][npx][npy] == -1) {
                    dp[bx][by][npx][npy] = dp[bx][by][px][py];
                    arrayDeque.addFirst(new Node(bx, by, npx, npy));
                }
            }
            
            // move box add back;
            if(Math.abs(bx - px) + Math.abs(by - py) == 1) {
                for(int[] dir: dirs) {
                    if(px + dir[0] == bx && py + dir[1] == by) {
                        int nbx = bx + dir[0];
                        int nby = by + dir[1];
                        if(0 <= nbx && nbx < m && 0 <= nby && nby < n && grid[nbx][nby] == '.'
                          && dp[nbx][nby][px][py] == -1) {
                            dp[nbx][nby][px][py] = dp[bx][by][px][py] + 1;
                            arrayDeque.offer(new Node(nbx, nby, px, py));
                        }
                    }
                }
            }
        }
        return -1;
    }
}