Shortest Path Visiting All Nodes-CSDN博客

本文链接：https://blog.csdn.net/u013325815/article/details/124792100

本文介绍了一种使用广度优先搜索(BFS)解决无向连通图中寻找包含所有节点的最短路径问题的方法。通过维护节点状态并避免重复路径，算法能够在找到遍历所有节点的路径时返回步数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

Example 1:

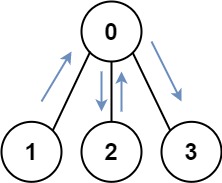
Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

思路：就是bfs，但是不同的是，要记录visited node的state，因为经过一个点的history可以有很多种，所以要用 state |= 1<<i 来记录；

class Solution {
    public int shortestPathLength(int[][] graph) {
        int n = graph.length;
        int finalstate = 0;
        for(int i = 0; i < n; i++) {
            finalstate |= (1 << i);
        }
        //                   node.id, state
        Queue<int[]> queue = new LinkedList<>();
        HashMap<Integer, HashSet<Integer>> visitedmap = new HashMap<>();
        
        for(int i = 0; i < n; i++) {
            queue.offer(new int[]{i, (1 << i)});
            visitedmap.put(i, new HashSet<>());
            visitedmap.get(i).add(1 << i);
        }
        
        int step = 0;
        while(!queue.isEmpty()) {
            int size = queue.size();
            for(int i = 0; i < size; i++) {
                int[] node = queue.poll();
                if(node[1] == finalstate) {
                    return step;
                }
                for(int neighbor: graph[node[0]]) {
                    int nextstate = node[1] | (1 << neighbor);
                    if(visitedmap.containsKey(neighbor) && visitedmap.get(neighbor).contains(nextstate)) {
                        continue;
                    }
                    visitedmap.get(neighbor).add(nextstate);
                    queue.offer(new int[]{neighbor, nextstate});
                }
            }
            step++;
        }
        return 0;
    }
}