POJ1038Bugs Integrated, Inc.
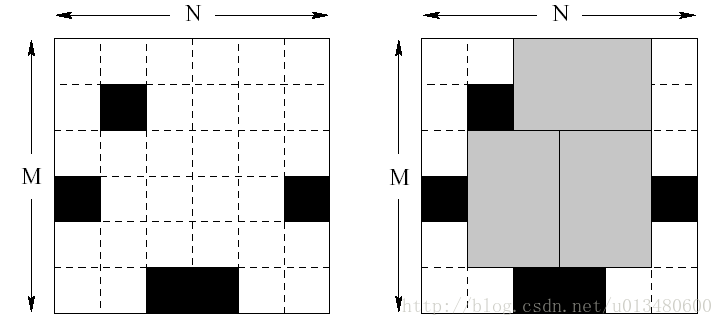
现在给你一个N*M的矩阵,然后矩阵有K个坏了的格子,矩阵中黑格子表示坏的格子,要你在所有好的格子中选出尽量多的2*3(或3*2)小矩阵,问你最多能选多少个这样的小矩阵.
输入:首先是一个t,(1<=t<=5)表示实例个数.对于每个实例,第一行是N,M和K,N (1<= N <= 150), M (1 <= M <= 10), K (0 <= K <= MN).接下来K行每行一对坐标x和y,表示(x,y)格是坏的.
输出:输出最多能选多少个2*3小矩阵.
分析:由题意我们可知假设从上到下开始摆放2*3(或3*2,后文统称为小矩阵)矩阵,那么当我们放到第i行的时候(我们只以当前格作为小矩阵的右下角摆放),当前行如何摆放只和第i-1和i-2行的摆放方式有关.
对于n*m矩阵,我们把已经摆放了小矩阵的格子填1,没摆放的填2.令d[i][S1][S2]=x,表示当前第i行的填充状态为S1,第i-1行的填充状态为S2时,此时前i行能放最多小矩阵数目为x个.
d[i+1][S1][S2]=max{d[i][S3][S4]+ get(i+1,S3,S4)},尝试在第i+1行每个格子放下向左或向上的小矩阵,生成新的S1和S2状态以及对应的格子数目.其中S2状态是由S3状态生成的.get(i+1,S3,S4)表示从d[i][S3][S4]生成d[i+1][S1][S2]最多能新摆放多少个小矩阵.
初值是:d[1][S1][S2]=x,初值通过模拟摆放方式计算出来.其他d值初始化为-1,标记未计算状态.
代码:测试结果正确,速度也够快但是内存溢出
//测试了多组数据结果都正确速度也够快的程序,但是内存要求太多溢出
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define base(i,j) base[i][j]
int n,m,bad,cnt;
int d[155][1<<10][1<<10];
int g[155][11];//保存初始矩阵
int state[300];//该state[i]=s保存的是一个三进制数,s的第i位为0表示不放,第i位为1表示左方,第i位为2表示上方
int mi[12];//幂运算
int base[60000][12];//base[x][i]=2,x的三进制形式的第i位是2
int sum;//记录最大能摆放的数目
char s_2[15];//用于打印数的三进制形式测试中间结果
char *print_2(int x)//保存x的二进制形式到s_2中,且x的第0位对应第0列,对应s_2中的第0位中.
{
for(inti=0;i<15;i++)
s_2[i]='0';
int p=0;
while(x)
{
s_2[p++]='0'+x%2;//x的第0位对应第0列,保存在s_2的第0位中
x/=2;
}
s_2[m]='\0';
return s_2;
}
char s_3[15];//用于打印数的三进制形式测试中间结果
char *print_3(int x)//保存x的三进制形式到s_3中,且x的第0位对应第0列,对应s_3中的第0位中.
{
for(int i=0;i<15;i++)
s_3[i]='0';
int p=0;
while(x)
{
s_3[p++]='0'+x%3;//x的第0位对应第0列,保存在s_3的第0位中
x/=3;
}
s_3[m]='\0';
return s_3;
}
inline bool good(int S)//判断状态S(三进制)是否合理,即在m个格子都是好格的情况下,能出现S状态的摆放
//s的第i位为0表示不放,第i位为1表示左方,第i位为2表示上方
{
for(int i=0;i<m;i++)//依次判断S的三进制中的每一位是1还是2就行
{
if(base[S][i]==1)//放的左矩阵
{
if(i<=1)//第1个和0个格子放不下左矩阵
return false;
if( base[S][i-1]!=0||base[S][i-2]!=0 )//此时i>=2,但是他的前两个格子已放
return false;
}
else if(base[S][i]==2)//放的上矩阵
{
if(i<=0)//第0个格子放不下上矩阵
return false;
if( base[S][i-1]!=0 )//此时i>=1,但是他的前一个格子已放
return false;
}
}
return true;
}
bool no_up(int S)//S的三进制形式表示的摆放方式没有任何上放
{
for(int i=0;i<m;i++)
if(base[S][i]==2)
return false;
return true;
}
inline bool legal(int S,int r,int S3,intS4)//要求r>=1判断S的三进制摆放状态在第r行且以S3和S4的二进制填充条件下是否合法
{//关于S3和S4是否分别满足如r-1行和r-2行给的初始矩阵,我们不管,我们假设他们已经满足了
//但是要注意当按照S摆放之后 生成的S1和S2要符合r和r-1行的初始矩阵
for(int i=0;i<m;i++)
{
if(base[S][i]==1)//此格左放,要考虑它的前两列格子和上一行格子,还有它本身
{
if(g[r][i]==0 || g[r][i-1]==0 ||g[r][i-2]==0)//r行的3列不合法
return false;
if(r<=0 || g[r-1][i]==0 || g[r-1][i-1]==0 || g[r-1][i-2]==0)//r-1行的3列不合法
return false;
if( ( S3&(1<<i) ) || ( S3&(1<< (i-1) ) ) || (S3&(1<< (i-2) ) ) )//上一行兼容
return false;
}
if(base[S][i]==2)//此格上放,要考虑它的前一列和上两行,包括它本身
{
if(g[r][i]==0 || g[r][i-1]==0)//r行的2列不合法
return false;
if(r<=0 || g[r-1][i]==0 || g[r-1][i-1]==0)//r-1行的2列不合法
return false;
if(r<=1 || g[r-2][i]==0 || g[r-2][i-1]==0)//r-2行的2列不合法
return false;
if( ( S3&(1<<i) ) || ( S3&(1<< (i-1) ) ) || (S4&(1<< (i) ) ) || ( S4&(1<< (i-1) ) ) )
//上两行兼容
return false;
}
}
return true;
}
void play(int r,int S3,int S4)//尝试摆放第r行(第r-1行和r-2行状态为S3和S4),并更新d[r][S1][S2]
{
for(int i=0;i<cnt;i++)if( legal(state[i],r,S3,S4) )//对于每一种预先生成的合理且合法状态
{
int S1=0,S2=S3;
int num=0;//记录当前行新摆放了几个小矩阵
for(int j=0;j<m;j++)//根据state[i]的三进制摆放状态生成当前行和上一行的状态
{
if(base[state[i]][j]==1)//第j列左放
{
S1 =S1|(1<<j)|(1<<(j-1) )|(1<<(j-2) );
S2 =S2|(1<<j)|(1<<(j-1) )|(1<<(j-2) );
num++;
}
else if(base[state[i]][j]==2)//第j列上放,不用更新第r-2行的S4,因为我们的d状态只需要用到前两行
{
S1 =S1|(1<<j)|(1<<(j-1) );
S2 = S2|(1<<j)|(1<<(j-1));
num++;
}
}
d[r][S1][S2]=max(d[r][S1][S2],d[r-1][S3][S4]+num);
//printf("d[%d][%s][%s]=%d 摆放:%s",r,print_2(S1),print_2(S2),d[r][S1][S2],print_3(state[i]));
//printf(" S3=%s S4=%s\n",print_2(S3),print_2(S4));
//printf("d[%d][%s][%s]=%d",r,print_2(S1),print_2(S2),d[r][S1][S2]);
//printf("当前选中的摆放状态为state[%d]=%s,且state_num[%d]为%d ",i,print_3(state[i]),i,state_num[i]);
//if(d[r][S1][S2] == d[r-1][S3][S4]+state_num[i])
// printf(" 由 d[%d][%s][%s]=%d 生成\n",r-1,print_2(S3),print_2(S4),d[r-1][S3][S4]);
//else
// printf("不由 d[%d][%s][%s]=%d 生成\n",r-1,print_2(S3),print_2(S4),d[r-1][S3][S4]);
if(r==n-1) sum = max(sum , d[r][S1][S2]);//取得最大值
}
}
void play_1()//更新d的第1行和第2行状态,即d的初始状态,行号从0开始计数.
{
int S3=0;//放第1行前 第0行的填充状态
int S4=(1<<m)-1;//放第1行前 第-1行的填充状态为全1
int r=1;//行号
for(int i=0;i<cnt;i++)if( legal(state[i],r,S3,S4) )//对于每一种预先生成的合理(good)且合法(legal)且与S3S4(legal)兼容三进制摆放状态
{//no_up()用来限制第一行的摆放不会出现任何上放的情况
int S1=0,S2=S3;
int num=0;//记录当前行新摆放了几个小矩阵
for(int j=0;j<m;j++)//根据state[i]的三进制摆放状态生成当前行和上一行的状态
{
if(base[state[i]][j]==1)//在第1行的第j列只能左放不能上放
{
S1 =S1|(1<<j)|(1<<(j-1) )|(1<<(j-2) );
S2 =S2|(1<<j)|(1<<(j-1) )|(1<<(j-2) );
num++;
}
/*
else if(base[state[i]][j]==2)//在第j列上放,不用更新第r-2行的S4,因为我们的d状态只需要用到前两行
{
S1 =S1|(1<<j)|(1<<(j-1) );
S2 =S2|(1<<j)|(1<<(j-1) );
}
*/
}
d[r][S1][S2]=max(d[r][S1][S2],num);
//printf("d[%d][%s][%s]=%d\n",r,print_2(S1),print_2(S2),d[r][S1][S2]);
if(n==2) sum = max(sum , d[r][S1][S2]);//如果只有两行,那么这就是最大值
}
}
int main()
{
//freopen("out.txt", "w", stdout);
int temp=1;
for(int i=0;i<=10;i++)
{
mi[i]=temp;
temp*=3;
}
for(int value=0;value<mi[10];value++)
{
temp = value;
int p =0;
while(temp>0)
{
base[value][p++]=temp%3;
temp/=3;
}
}
intT;
while(scanf("%d",&T)==1&&T)
{
while(T--)
{
sum = 0;//最大值初始化
scanf("%d%d%d",&n,&m,&bad);
if(n==1)//只有一行时特殊处理
{
printf("0\n");
continue;
}
for(int i=0;i<n;i++)//此处可以改成 memset(g,1,sizeof(g)); 吗?
for(int j=0;j<m;j++)
g[i][j]=1;
for(int i=0;i<bad;i++)
{
int a,b;
scanf("%d%d",&a,&b);
a--;b--;
g[a][b]=0;//坏格子标记为1
}
cnt = 0;
for(int S=0;S<mi[m];S++)//预先生成所有合理的三进制摆放状态,在m个格子都是好格子的时候能放下就行
{
if(good(S))
{
state[cnt++]=S;
}
}
//printf("m=%d cnt=%d\n",m,cnt);
memset(d,-1,sizeof(d));
play_1();//生成d[1][][]的初始值,即第一行的d所有可能的值,行数从0开始计数
for(int r=2;r<n;r++)
{
for(intS3=0;S3<(1<<m);S3++)//S3的二进制形式是第r-1行的填充状态
{
for(intS4=0;S4<(1<<m);S4++)//S4的二进制形式是第r-2行的填充状态
{
if(d[r-1][S3][S4]==-1)//(r-1,S3,S4)是一个非法的不可生成 的状态
continue;
play(r,S3,S4);
}
}
}
printf("%d\n",sum);
}
}
return 0;
}
第二份代码:超时 但是我测试的速度还可以,这份代码使用滚动数组把需要的内存缩小了很多,但是还是超时.
//测试了多组数据结果都正确速度也够快的程序,但是内存要求太多溢出
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int cur_r;
int n,m,bad,cnt;
int d[2][1<<10][1<<10];
int g[155][11];//保存初始矩阵
int state[300];//该state[i]=s保存的是一个三进制数,s的第i位为0表示不放,第i位为1表示左方,第i位为2表示上方
int mi[12];//幂运算
//int base[60000][12];//base[x][i]=2,x的三进制形式的第i位是2
int sum;//记录最大能摆放的数目
int base(int S,int i)//得到状态S的三进制形式的第i位
{
for(int j=0;j<i;j++)
{
S=S/3;
}
return S%3;
}
char s_2[15];//用于打印数的三进制形式测试中间结果
char *print_2(int x)//保存x的二进制形式到s_2中,且x的第0位对应第0列,对应s_2中的第0位中.
{
for(int i=0;i<15;i++)
s_2[i]='0';
int p=0;
while(x)
{
s_2[p++]='0'+x%2;//x的第0位对应第0列,保存在s_2的第0位中
x/=2;
}
s_2[m]='\0';
return s_2;
}
char s_3[15];//用于打印数的三进制形式测试中间结果
char *print_3(int x)//保存x的三进制形式到s_3中,且x的第0位对应第0列,对应s_3中的第0位中.
{
for(int i=0;i<15;i++)
s_3[i]='0';
int p=0;
while(x)
{
s_3[p++]='0'+x%3;//x的第0位对应第0列,保存在s_3的第0位中
x/=3;
}
s_3[m]='\0';
return s_3;
}
inline bool good(int S)//判断状态S(三进制)是否合理,即在m个格子都是好格的情况下,能出现S状态的摆放
//s的第i位为0表示不放,第i位为1表示左方,第i位为2表示上方
{
for(int i=0;i<m;i++)//依次判断S的三进制中的每一位是1还是2就行
{
if(base(S,i)==1)//放的左矩阵
{
if(i<=1)//第1个和0个格子放不下左矩阵
return false;
if( base(S,i-1)!=0||base(S,i-2)!=0 )//此时i>=2,但是他的前两个格子已放
return false;
}
else if(base(S,i)==2)//放的上矩阵
{
if(i<=0)//第0个格子放不下上矩阵
return false;
if( base(S,i-1)!=0 )//此时i>=1,但是他的前一个格子已放
return false;
}
}
return true;
}
bool no_up(int S)//S的三进制形式表示的摆放方式没有任何上放
{
for(int i=0;i<m;i++)
if(base(S,i)==2)
return false;
return true;
}
inline bool legal(int S,int r,int S3,intS4)//要求r>=1判断S的三进制摆放状态在第r行且以S3和S4的二进制填充条件下是否合法
{//关于S3和S4是否分别满足如r-1行和r-2行给的初始矩阵,我们不管,我们假设他们已经满足了
//但是要注意当按照S摆放之后 生成的S1和S2要符合r和r-1行的初始矩阵
for(int i=0;i<m;i++)
{
if(base(S,i)==1)//此格左放,要考虑它的前两列格子和上一行格子,还有它本身
{
if(g[r][i]==0 || g[r][i-1]==0 || g[r][i-2]==0)//r行的3列不合法
return false;
if(r<=0 || g[r-1][i]==0 || g[r-1][i-1]==0 || g[r-1][i-2]==0)//r-1行的3列不合法
return false;
if( ( S3&(1<<i) ) || ( S3&(1<< (i-1) ) ) || (S3&(1<< (i-2) ) ) )//上一行兼容
return false;
}
if(base(S,i)==2)//此格上放,要考虑它的前一列和上两行,包括它本身
{
if(g[r][i]==0 || g[r][i-1]==0)//r行的2列不合法
return false;
if(r<=0 || g[r-1][i]==0 || g[r-1][i-1]==0)//r-1行的2列不合法
return false;
if(r<=1 || g[r-2][i]==0 || g[r-2][i-1]==0)//r-2行的2列不合法
return false;
if( ( S3&(1<<i) ) || ( S3&(1<< (i-1) ) ) || (S4&(1<< (i) ) ) || ( S4&(1<< (i-1) ) ) )
//上两行兼容
return false;
}
}
return true;
}
void play(int r,int S3,int S4)//尝试摆放第r行(第r-1行和r-2行状态为S3和S4),并更新d[r][S1][S2]
{
for(int i=0;i<cnt;i++)if( legal(state[i],r,S3,S4) )//对于每一种预先生成的合理且合法状态
{
int S1=0,S2=S3;
int num=0;//记录当前行新摆放了几个小矩阵
for(int j=0;j<m;j++)//根据state[i]的三进制摆放状态生成当前行和上一行的状态
{
if(base(state[i],j)==1)//第j列左放
{
S1 =S1|(1<<j)|(1<<(j-1) )|(1<<(j-2) );
S2 =S2|(1<<j)|(1<<(j-1) )|(1<<(j-2) );
num++;
}
else if(base(state[i],j)==2)//第j列上放,不用更新第r-2行的S4,因为我们的d状态只需要用到前两行
{
S1 =S1|(1<<j)|(1<<(j-1) );
S2 =S2|(1<<j)|(1<<(j-1) );
num++;
}
}
d[cur_r][S1][S2]=max(d[cur_r][S1][S2],d[1-cur_r][S3][S4]+num);
//printf("d[%d][%s][%s]=%d 摆放:%s",r,print_2(S1),print_2(S2),d[r][S1][S2],print_3(state[i]));
//printf(" S3=%sS4=%s\n",print_2(S3),print_2(S4));
//printf("d[%d][%s][%s]=%d",r,print_2(S1),print_2(S2),d[r][S1][S2]);
//printf("当前选中的摆放状态为state[%d]=%s,且state_num[%d]为%d ",i,print_3(state[i]),i,state_num[i]);
//if(d[r][S1][S2] == d[r-1][S3][S4]+state_num[i])
// printf(" 由 d[%d][%s][%s]=%d 生成\n",r-1,print_2(S3),print_2(S4),d[r-1][S3][S4]);
//else
// printf("不由 d[%d][%s][%s]=%d 生成\n",r-1,print_2(S3),print_2(S4),d[r-1][S3][S4]);
if(r==n-1) sum = max(sum , d[cur_r][S1][S2]);//取得最大值
}
}
void play_1()//更新d的第1行和第2行状态,即d的初始状态,行号从0开始计数.
{
int S3=0;//放第1行前 第0行的填充状态
int S4=(1<<m)-1;//放第1行前 第-1行的填充状态为全1
int r=1;//行号
for(int i=0;i<cnt;i++)if( legal(state[i],r,S3,S4) )//对于每一种预先生成的合理(good)且合法(legal)且与S3S4(legal)兼容三进制摆放状态
{//no_up()用来限制第一行的摆放不会出现任何上放的情况
int S1=0,S2=S3;
int num=0;//记录当前行新摆放了几个小矩阵
for(int j=0;j<m;j++)//根据state[i]的三进制摆放状态生成当前行和上一行的状态
{
if(base(state[i],j)==1)//在第1行的第j列只能左放不能上放
{
S1 =S1|(1<<j)|(1<<(j-1) )|(1<<(j-2) );
S2 =S2|(1<<j)|(1<<(j-1) )|(1<<(j-2) );
num++;
}
/*
else if(base[state[i]][j]==2)//在第j列上放,不用更新第r-2行的S4,因为我们的d状态只需要用到前两行
{
S1 =S1|(1<<j)|(1<<(j-1) );
S2 =S2|(1<<j)|(1<<(j-1) );
}
*/
}
d[r][S1][S2]=max(d[r][S1][S2],num);
//printf("d[%d][%s][%s]=%d\n",r,print_2(S1),print_2(S2),d[r][S1][S2]);
if(n==2) sum = max(sum , d[r][S1][S2]);//如果只有两行,那么这就是最大值
}
}
int main()
{
//freopen("out.txt", "w", stdout);
int temp=1;
for(int i=0;i<=10;i++)
{
mi[i]=temp;
temp*=3;
}
/*
for(int value=0;value<mi[10];value++)
{
temp = value;
int p =0;
while(temp>0)
{
base[value][p++]=temp%3;
temp/=3;
}
}
*/
int T;
while(scanf("%d",&T)==1&&T)
{
while(T--)
{
sum = 0;//最大值初始化
scanf("%d%d%d",&n,&m,&bad);
if(n==1)//只有一行时特殊处理
{
printf("0\n");
continue;
}
for(int i=0;i<n;i++)//此处可以改成 memset(g,1,sizeof(g)); 吗?
for(int j=0;j<m;j++)
g[i][j]=1;
for(int i=0;i<bad;i++)
{
int a,b;
scanf("%d%d",&a,&b);
a--;b--;
g[a][b]=0;//坏格子标记为1
}
cnt = 0;
for(int S=0;S<mi[m];S++)//预先生成所有合理的三进制摆放状态,在m个格子都是好格子的时候能放下就行
{
if(good(S))
{
state[cnt++]=S;
}
}
//printf("m=%d cnt=%d\n",m,cnt);
memset(d,-1,sizeof(d));
play_1();//生成d[1][][]的初始值,即第一行的d所有可能的值,行数从0开始计数
cur_r=1;
for(int r=2;r<n;r++)
{
cur_r = 1-cur_r;
for(intS3=0;S3<(1<<m);S3++)//S3的二进制形式是第r-1行的填充状态
{
for(intS4=0;S4<(1<<m);S4++)//S4的二进制形式是第r-2行的填充状态
{
if(d[1-cur_r][S3][S4]==-1)//(r-1,S3,S4)是一个非法的不可生成 的状态
continue;
play(r,S3,S4);
}
}
}
printf("%d\n",sum);
}
}
return 0;
}通过分析,使用轮廓线动态规划来算和上面的二行DP复杂度基本一样,估计还是超时.
新的解法:
通过分析我们知道当前第i行能不能放左上矩阵只与第i-1行和第i-2行有关,且如果第i-1行是坏格或者被占用的话即使第i-2行的对应格子是空的也没用.所以我们归纳下面3种表示状态:
1. 第(i-1,j)格空闲,第(i-2,j)格空闲,此两个表示一个0
2. 第(i-1,j)格空闲,第(i-2,j)格占用,此两个表示一个1
3. 第(i-1,j)格占用,此格和第(i-2,j)格表示一个2
则我们用一个三进制数就可以表示前两行的所有状态了.
| 占用 | 空闲 | 空闲 | 占用 |
| 空闲 | 占用 | 空闲 | 占用 |
上面两行的状态用一个三进制数表示就是S=2021,此数十进制为31.注意S的三进制形式的第0位数字表示的是矩阵第0列的状态而不是最后一列.即S中的1表示的是矩阵第一列(空闲,占用)的状态.
令d[cur][S]=x表示当前行以及前一行的状态是S时,最多能摆x个小矩阵.状态转移方程是:
d[cur][S]= max{ d[1-cur][S1] } 其中1-cur表示上一列生成的状态,cur表示当前列处理的状态,并且状态S是可以通过摆放当前行来将S1的下一行加上当前行转化为S的.
初值:d[0][<11111>]=0.
代码:测试几组结果正确,但是依然超时.
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,bad,cnt,sum,cur;
int d[2][60000];
int g[155][11];
int mi[12];//幂运算
int base[60000][12];//base[x][i]=2,x的三进制形式的第i位是2
int state[300];//该state[i]=s保存的是一个三进制数,s的第i位为0表示不放,第i位为1表示左方,第i位为2表示上方
inline bool good(int S)//判断状态S(三进制)是否合理,即在m个格子都是好格的情况下,能出现S状态的摆放
//s的第i位为0表示不放,第i位为1表示左方,第i位为2表示上方
{
for(int i=0; i<m; i++) //依次判断S的三进制中的每一位是1还是2就行
{
if(base[S][i]==1)//放的左矩阵
{
if(i<=1)//第1个和0个格子放不下左矩阵
return false;
if( base[S][i-1]!=0||base[S][i-2]!=0 )//此时i>=2,但是他的前两个格子已放
return false;
}
else if(base[S][i]==2)//放的上矩阵
{
if(i<=0)//第0个格子放不下上矩阵
return false;
if( base[S][i-1]!=0 )//此时i>=1,但是他的前一个格子已放
return false;
}
}
return true;
}
bool legal(int r,int S,int S2)//判断摆放方式S是否和g[r]且和前两行的联合状态S2都兼容,S在这里是摆放状态不是联合状态
{
//关于S2是否分别满足如r-1行和r-2行给的初始矩阵,我们不管,我们假设他已经满足了
//但是要注意当按照S摆放之后 生成的S1联合状态要符合r和r-1行的初始矩阵
for(int i=0; i<m; i++) //第i列
{
if(base[S][i]==1)//此格左放,要考虑它的前两列格子和上一行格子,还有它本身
{
if(g[r][i]==0 || g[r][i-1]==0 || g[r][i-2]==0)//r行的3列不合法
return false;
if(r<=0 || g[r-1][i]==0 || g[r-1][i-1]==0 || g[r-1][i-2]==0)//r-1行的3列不合法
return false;
if( base[S2][i]==2 || base[S2][i-1]==2 || base[S2][i-2]==2 )//联合状态第i,i-1,i-2位至少有一位是2
return false;
}
if(base[S][i]==2)//此格上放,要考虑它的前一列和上两行,包括它本身
{
if(g[r][i]==0 || g[r][i-1]==0)//r行的2列不合法
return false;
if(r<=0 || g[r-1][i]==0 || g[r-1][i-1]==0)//r-1行的2列不合法
return false;
if(r<=1 || g[r-2][i]==0 || g[r-2][i-1]==0)//r-2行的2列不合法
return false;
if( base[S2][i]!=0 || base[S2][i-1]!=0 )
//联合状态第i位或第i-1位不是1就是2
return false;
}
}
return true;
}
bool legal_1(int S,int S2)//判断摆放方式S是否和g[0]和g[1]且和前两行的联合状态S2都兼容,S在这里是摆放状态不是联合状态
{
//关于S2是否分别满足如r-1行和r-2行给的初始矩阵,我们不管,我们假设他已经满足了
//但是要注意当按照S摆放之后 生成的S1联合状态要符合r和r-1行的初始矩阵
int r=1;
for(int i=0; i<m; i++) //第i列
{
if(base[S][i]==1)//此格左放,要考虑它的前两列格子和上一行格子,还有它本身
{
if(g[r][i]==0 || g[r][i-1]==0 || g[r][i-2]==0)//r行的3列不合法
return false;
if(r<=0 || g[r-1][i]==0 || g[r-1][i-1]==0 || g[r-1][i-2]==0)//r-1行的3列不合法
return false;
if( base[S2][i]==2 || base[S2][i-1]==2 || base[S2][i-2]==2 )//联合状态第i,i-1,i-2位至少有一位是2
return false;
}
if(base[S][i]==2)//此格上放,要考虑它的前一列和上两行,包括它本身
{
return false;
}
}
return true;
}
void play(int r,int S1)//当前处理第r行,且前两行(r-1和r-2)的联合状态是S1的三进制形式
{
for(int i=0; i<cnt; i++)if(legal(r,state[i],S1)) //要求state[i]与g[r]兼容,且与S1兼容
{
int S=0;
int num = 0;//计算摆放了多少个小矩阵
for(int j=0; j<m; j++) //根据state[i]的三进制摆放状态生成当前行和上一行的联合状态
{
if(base[state[i]][j]==1)//第j列左放,新联合状态第j,j-1,j-2位都置2
{
S +=2*mi[j]+2*mi[j-1]+2*mi[j-2];
num++;
}
elseif(base[state[i]][j]==2)//第j列上放,新联合状态第j,j-1位都置2
{
S += 2*mi[j]+2*mi[j-1];
num++;
}
}
for(int j=0; j<m; j++) //根据联合状态S1的第1行更新当前行联合状态S的初始状态
{
if(base[S1][j]==2 &&base[S][j]==0)//第r-1行j列被填充,但是第r行的j列为空,那么联合状态S第j位置1
S += mi[j];
}
d[cur][S]=max(d[cur][S],d[1-cur][S1]+num);
if(r==n-1) sum = max(sum , d[cur][S]);//取得最大值
}
}
void play_1()//当前处理第1行,且前两行0行和假象行的联合状态是S1的三进制形式=1111111 (3)
{
//int r = 1;
int S1 = 0;
for(int i=0; i<m; i++) //S1为全1
S1 += mi[i];
for(int i=0; i<cnt; i++)if(legal_1(state[i],S1)) //要求state[i]与第1行和第0行的g兼容,且与S1兼容
{
int S=0;
int num = 0;//计算摆放了多少个小矩阵
for(int j=0; j<m; j++) //根据state[i]的三进制摆放状态生成当前行和上一行的联合状态
{
if(base[state[i]][j]==1)//第j列左放,新联合状态第j,j-1,j-2位都置2
{
S +=2*mi[j]+2*mi[j-1]+2*mi[j-2];
num++;
}
else if(base[state[i]][j]==2)//第j列上放,新联合状态第j,j-1位都置2
{
S += 2*mi[j]+2*mi[j-1];
num++;
}
}
for(int j=0; j<m; j++) //根据联合状态S1的第1行更新当前行联合状态S的初始状态
{
if(base[S1][j]==2 &&base[S][j]==0)//第r-1行j列被填充,但是第r行的j列为空,那么联合状态S第j位置1
S += mi[j];
}
d[1][S]=max(d[1][S],num);
if(n==2) sum = max(sum , d[1][S]);//取得最大值
}
}
int main()
{
int temp=1;//预处理幂运算相关
for(int i=0; i<=10; i++)
{
mi[i]=temp;
temp*=3;
}
for(int value=0; value<mi[10]; value++)
{
temp = value;
int p =0;
while(temp>0)
{
base[value][p++]=temp%3;
temp/=3;
}
}
int T;
while(scanf("%d",&T)==1&&T)
{
while(T--)
{
sum = 0;//最大值初始化
scanf("%d%d%d",&n,&m,&bad);
if(n==1)//只有一行时特殊处理
{
printf("0\n");
continue;
}
for(int i=0; i<n; i++) //此处可以改成 memset(g,1,sizeof(g)); 吗?
for(int j=0; j<m; j++)
g[i][j]=1;
for(int i=0; i<bad; i++)
{
int a,b;
scanf("%d%d",&a,&b);
a--;
b--;
g[a][b]=0;//坏格子标记为0
}
cnt = 0;
for(int S=0; S<mi[m]; S++) //预生成所有合理的三进制摆放状态,在m个格子都是好格子的时候能放下就行
{
if(good(S))
{
state[cnt++]=S;
}
}
//printf("m=%d cnt=%d\n",m,cnt);
memset(d,-1,sizeof(d));
play_1();//生成d[1][]的所有初始合法状态值
cur = 1;
for(int r=2; r<n; r++)
{
cur = 1- cur;
for(int S1=0; S1<mi[m];S1++) //S1的二进制形式是第r-1行的填充状态
{
if(d[1-cur][S1]==-1)//(r-1,S1)是一个非法的不可生成 的状态
continue;
play(r,S1);
}
}
printf("%d\n",sum);
}
}
return 0;
}
现在使用三进制表示前两行的联合状态且使用滚动数组,还要使用dfs搜索可行的摆放状态(不能用枚举,用枚举超时).
AC代码:dfs放右上矩阵1829ms dfs放左上矩阵2000ms
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,bad,sum,cur;
int d[2][60000];
int g[155][11];
int mi[12];//幂运算
int base[60000][12];//base[x][i]=2,x的三进制形式的第i位是2
int state[300];//该state[i]=s保存的是一个三进制数,s的第i位为0表示不放,第i位为1表示左方,第i位为2表示上方
char s_3[15];//用于打印数的三进制形式测试中间结果
char *print_3(int x)//保存x的三进制形式到s_3中,且x的第0位对应第0列,对应s_3中的第0位中.
{
for(int i=0;i<15;i++)
s_3[i]='0';
int p=0;
while(x)
{
s_3[p++]='0'+x%3;//x的第0位对应第0列,保存在s_3的第0位中
x/=3;
}
s_3[m]='\0';
return s_3;
}
int P,Q;
void dfs(int r,int c,int num)//决策到r行c列 目前的d[][]=num
{
if(c==m)return ;
d[cur][Q]=max(d[cur][Q],num);
//printf("0: d[%d][%s]=%d***P=%s***Q=%s\n",r,print_3(Q),d[cur][Q],print_3(P),print_3(Q));
//上放
if(c<=m-2&&base[P][c]==0&&base[P][c+1]==0&&base[Q][c]==0&&base[Q][c+1]==0)
{
Q += 2*mi[c];
Q += 2*mi[c+1];
d[cur][Q]=max(d[cur][Q],num+1);
//printf("1: d[%d][%s]=%d***P=%s***Q=%s\n",r,print_3(Q),d[cur][Q],print_3(P),print_3(Q));
dfs(r,c+2,num+1);
Q -= 2*mi[c];
Q -= 2*mi[c+1];
}
//右放
if(c<=m-3&&base[Q][c]==0&&base[Q][c+1]==0&&base[Q][c+2]==0)
{
Q += 2*mi[c];
Q += 2*mi[c+1];
Q += 2*mi[c+2];
d[cur][Q]=max(d[cur][Q],num+1);
//printf("2: d[%d][%s]=%d***P=%s***Q=%s\n",r,print_3(Q),d[cur][Q],print_3(P),print_3(Q));
dfs(r,c+3,num+1);
Q -= 2*mi[c];
Q -= 2*mi[c+1];
Q -= 2*mi[c+2];
}
dfs( r, c+1, num );
}
int main()
{
//freopen("mytest.out", "w", stdout);
int temp=1;//预处理幂运算相关
for(int i=0; i<=10; i++)
{
mi[i]=temp;
temp*=3;
}
for(int value=0; value<mi[10]; value++)
{
temp = value;
int p =0;
while(temp>0)
{
base[value][p++]=temp%3;
temp/=3;
}
}
int T;
while(scanf("%d",&T)==1&&T)
{
while(T--)
{
sum = 0;//最大值初始化
scanf("%d%d%d",&n,&m,&bad);
if(n==1)//只有一行时特殊处理
{
printf("0\n");
continue;
}
for(int i=0; i<n; i++) //此处可以改成 memset(g,1,sizeof(g)); 吗?
for(int j=0; j<m; j++)
g[i][j]=1;
for(int i=0; i<bad; i++)
{
int a,b;
scanf("%d%d",&a,&b);
a--;
b--;
g[a][b]=0;//坏格子标记为0
}
//printf("m=%d cnt=%d\n",m,cnt);
memset(d,-1,sizeof(d));
int S=0;
for(int i=0;i<m;i++)
{
if(g[0][i]==0) S+= 2*mi[i];
else S+= mi[i];
}
d[0][S]=0;//生成d[0][]的所有初始合法状态值
cur = 0;
for(int r=1; r<n; r++)
{
cur = 1- cur;
memset( d[cur], -1, sizeof(d[cur]) );
for(int S1=0; S1<mi[m]; S1++) //S1的二进制形式是第r-1行的填充状态
{
if(d[1-cur][S1]==-1)//(r-1,S1)是一个非法的 不可生成 的状态
continue;
//printf("d[%d][%s]=%d\n",r-1,print_3(S1),d[1-cur][S1]);
P = S1;
Q=0;
for(int i=0;i<m;i++)
{
if(g[r][i]==0)Q+= 2*mi[i];
else
{
int x;
x = base[P][i]-1;
if(x<0) x= 0;
Q+=x*mi[i];
}
}
dfs(r,0,d[1-cur][P]);//r行0列开始模拟摆放
//play(r,S1);
}
}
for(int S=0;S<mi[m];S++)
sum = max(sum,max(d[cur][S],d[1-cur][S]));
printf("%d\n",sum);
}
}
return 0;
}
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








