【转】关于相关性的7个最常见的问题

关于相关性的7个最常见的问题

作者：常龙
本文链接：https://zhuanlan.zhihu.com/p/38353751?ivk_sa=1024320u

• 感谢常龙的分享，仅作学术交流，如有侵权-联系后台删除~

觉得有用的话,欢迎一起讨论相互学习~

本文来源于7 most commonly asked questions on Correlation，经过翻译和修改后得到的，旨在帮助数据分析和挖掘人员了解相关性的知识，扫除关于相关性分析的知识盲点。

关于相关的7个最常见问题

介绍

学习统计的自然轨迹始于中心趋势分析，随后是相关性，回归再其他先进概念。在这些最初的概念中，我发现相关性很容易理解，但当它与其他统计概念和方法（如因果关系，回归，分布，皮尔逊相关系数等等）联系起来时，我们感到困惑不解。我花了一段时间才获得成功并得到坚定的结果在这个概念上。我成功了，因为我一直在努力尝试，每次失败后都会更加努力。因此，不要放弃，继续尝试！

首先，如果你仍然在努力理解相关性和因果关系的区别，你应该参考我以前的文章，我已经用最简单的方式解释了这些概念。

让我们继续进一步学习关于相关问题的最常见问题。如果你正在学习统计概念，你一定会面对这些大多数人试图避免的问题。对于像我这样的人来说，这应该是一个很好的进修。

在这里你会学到什么？

1. 相关性和依赖性是否意味着同样的事情？简而言之，如果两个事件的相关性为零，这是否表示它们不依赖，反之亦然？
2. 如果两个变量与第三个变量有很高的相关性，这是否表达它们也会高度相关？A和B是否可能与另一个变量C正相关？A和B可能是负相关的吗？
3. 单个异常值可以减少还是增加相关性？皮尔逊系数是否对异常值非常敏感？
4. 因果关系是否意味着相关？
5. 相关性和简单线性回归之间有什么区别？
6. 如何在皮尔逊和斯皮尔曼相关系数之间进行选择？
7. 你如何解释相关性和协方差之间的差异？

上述许多问题的答案可能看起来很直观，但是您可以在下面的文章中找到相应的答案。

理解相关系数的数学表达式

最广泛使用的相关系数是**皮尔逊系数。**这是推导Pearson系数的数学公式。

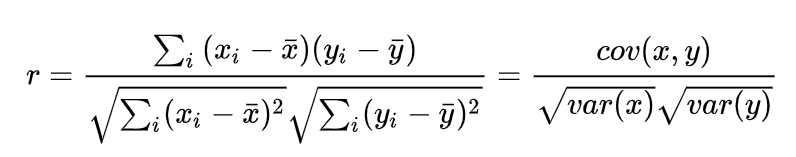
**说明：**它只是两个变量的协方差与（变量的）方差乘积的比率。它取值在+1和-1之间。两侧的极端值意味着它们彼此强相关。值为零表示零相关性，但不是非相关性。您将在以下答案之一中清楚地理解这一点。

斯皮尔曼等级相关系数：

上述中的d为两个序列对应值的差分值。

答案1：相关性与依赖性

两个变量之间的非相关意味着零相关。然而情况并非如此。零关联甚至可以具有完美的依赖关系。这里是一个例子：

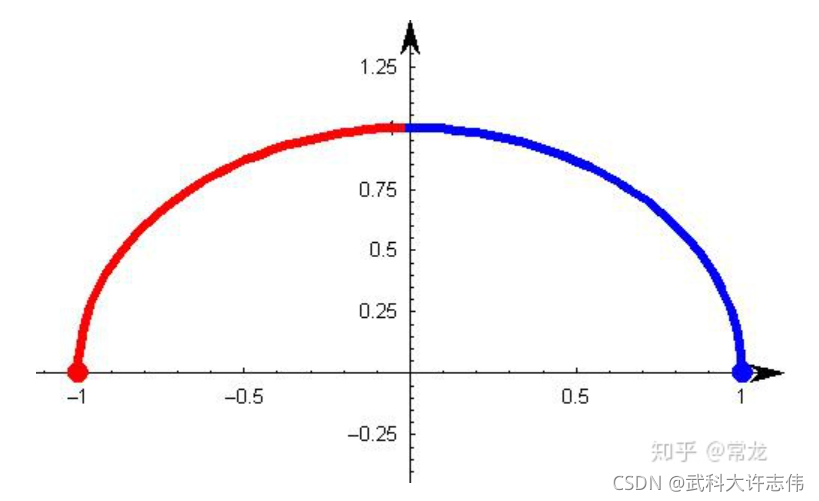
上图中的图像是函数

$y=\sqrt{1-x^2}$

x与y有明显的数据表达式，是非线性相关的，但是通过数学计算的皮尔逊相关系数为零，这是为什么？

**必须记住提示：**相关性量化了两个变量的线性相关性。它不能捕获两个变量之间的非线性关系。

良好阅读：必须在分析/数据科学中阅读图书

答案2：相关传递？

假设X，Y和Z是随机变量。X和Y正相关，Y和Z同样正相关。它是否遵循X和Z必须正相关？

正如我们将通过示例所看到的，答案（可能令人惊讶）是“ N o”。我们可以证明，如果相关性足够接近1，那么X和Z必须正相关。

我们假设C（x，y）是x和y之间的相关系数。像智慧一样，我们有C（x，z）和C（y，z）。下面是一个方程，它来自数学上求解相关方程：

C（x，y）= C（y，z）* C（z，x） - 平方根（（1-C（y，z）^ 2）*（1-C（z，x）^ 2））

现在，如果我们希望C（x，y）大于零，我们基本上希望以上方程的右边为正。因此，您需要解决以下问题：

C（y，z）* C（z，x）>平方根（（1-C（y，z）^ 2）*（1-C（z，x）^ 2））

我们实际上可以通过对两边进行平方来求解C（y，z）> 0和C（y，z）<0的上述方程。这将最终给出结果，如果下面的公式成立，则C（x，y）是非零数字：

C（y，z）^ 2 + C（z，x）^ 2> 1

哇，这是一个圈子的等式。因此下面的图解将解释一切：

如果两个已知的相关性在A区，则第三个相关性将是正的。如果他们位于B区，则第三个相关性将为负值。在圈子里面，我们不能说任何关系。这里有一个非常有趣的见解是，即使C（y，z）和C（z，x）是0.5，C（x，y）实际上也可以是负的。

答案3：皮尔逊系数是否对异常值敏感？

答案是肯定的。即使是单个异常值也可以改变系数的方向。这里有几个例子，它们的相关系数都是0.81：

考虑最后两张图（X3Y3和X4Y4）。X3Y3显然是一个完美关联的情况，其中一个异常值显着降低了系数。最后一个图完全相反，由于单个异常值，相关系数变为高正数。结论是，这是相关系数最大的问题，它受到异常值的高度影响。

答案 - 4：因果关系意味着相关性吗？

如果您已阅读我们的上述三个答案，我相信您将能够回答这个问题。答案是否定的，因为因果关系也可能导致非线性关系。让我们了解如何！

以下是显示从0到12摄氏度的水密度的图表。我们知道密度是温度变化的影响。但是，密度可以达到4摄氏度时的最大值。因此，它不会与温度呈线性关系。

答案5：相关和简单线性回归之间的区别

这两个非常接近。所以让我们从两个共同的东西开始。

• 皮尔逊相关系数的平方与简单线性回归中的平方相同
• 简单线性回归和相关性都不直接回答因果关系问题。这一点很重要，因为我遇到了人们认为简单的回归可以推断出因果关系。这是荒谬的信念。

相关性和简单线性回归之间有什么区别？

现在让我们来想一下两者之间的差别。简单的线性回归比Pearson Correlation提供了更多关于关系的信息。这里有一些东西通过回归会给出，但相关系数不会。

• 线性回归中的斜率通过将自变量改变为单位距离来给出输出/目标变量的边际变化。相关性没有斜率。
• 线性回归中的截距给出了目标变量的值，如果其中一个输入/自变量设置为零。相关性没有这个信息。
• 线性回归可以给你一个给定所有输入变量的预测。相关分析不能预测任何事情。

答案6：皮尔逊与斯皮尔曼

这里最简单的答案是Pearson捕获两个变量如何线性相关，而Spearman捕捉变量之间关系的单调行为。

例如考虑以下关系：

$y=exp(x)$

在这里，你会发现皮尔逊系数为0.25，但斯皮尔曼系数为1.作为一个拇指规则，当你有关于非线性关系的初始假设时，你应该只从斯皮尔曼开始。否则，我们通常首先尝试皮尔逊，如果这个比较低，试试斯皮尔曼。这样你就知道变量是线性相关的还是只有单调行为。

答案7：相关与协方差

如果您在本文开始时跳过了相关性的数学公式，现在是重新审视这个问题的时候了。

相关性只是两个因素的标准差的标准化协方差。这样做是为了确保我们得到一个介于+1和-1之间的数字。协方差难以比较，因为它取决于两个变量的单位。可能会出现这样的情况，即学生的标记与他的脚趾指甲的毫米数更相关，而不是他的出勤率。

这仅仅是因为第二个变量的单位不同。因此，我们认为有必要通过一些规范化将这种协变量归一化，以确保我们将苹果与苹果进行比较。这个标准化的数字被称为相关性。

结束笔记

相关问题在访谈中很常见。关键是要知道相关性是两个变量的线性相关性的估计。相关性对于有限范围的相关对是传递性的。它也受到异常值的高度影响。我们了解到，相关性既不意味着因果关系，反之亦然。