EOJ 1824 【动态规划】

/*题目链接*/

题意：有一个由正整数组成的三角形，如下：

1

      2   3

    4   5   6

  7   8   9   10

      .....

     从第一行开始向下走，每次只能向左下或者右下走一格，例如当前在5，下一步只能走到8或9。问如何走,使得结果的个位数最大，输出最大值。

题目分析：这题和经典的数塔问题很像，唯一的区别就是答案不是和最大而是个位数最大。如果我们延用F[i][j]表示(i,j)作为根能取到的最大个位数值，这种表示方法是不具有最优化性质的，也就是子问题的最优解推不出父问题的最优解。换一个角度思考，虽然我没法写出最大值之间的转移方程，但是我们可以知道以(i,j)为根能取到哪些个位数值。所以用F[i][j][0...9]表示状态，F的取值只有0或者1，表示能否取到。

这样最后的状态转移方程就是

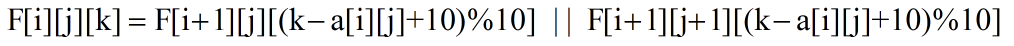
最后输出F[0][0][X]=True中最大的X就行。

AC代码：

<pre name="code" class="cpp">#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
int a[505][505] ,n;
bool f[505][505][10];
 
int main()
{
    int test;
    scanf("%d",&test);
    while (test--)
    {
        memset(f,0,sizeof(f));
        scanf("%d",&n);
        for (int i=0; i!=n; ++i)
            for (int j=0; j<=i; ++j)
                scanf("%d",&a[i][j]);
        for (int i=0; i<=n-1; ++i)
            f[n-1][i][a[n-1][i]%10] = true;
        for (int i=n-2; i>=0; --i)
            for (int j=0; j<=i; ++j)
                for (int k=0; k<=9; ++k)
                    f[i][j][k] = f[i+1][j][(k-a[i][j]%10+10)%10] || f[i+1][j+1][(k-a[i][j]%10+10)%10];
        for (int i=9; i>=0; --i)
            if (f[0][0][i])
            {
                printf("%d\n",i);
                break;
            }
    }
    return 0;
}