Number of permutation with K inversions

Given an array, an inversion is defined as a pair a[i], a[j] such that a[i] > a[j] and i < j. We are given two numbers N and k, we need to tell how many permutation of first N number have exactly K inversion.

给定一个数组，inversion被定义为a [i]，a [j]，使得[i]> a [j]和i < j。 我们给出两个数字N和k，我们需要计算出 N 个数的排列有多少个正好是K个inversion。

例如:
输入 : N = 3, K = 1
输出 : 2
Explanation :
全部的可能情况：
123, 132, 213, 231, 312, 321
符合条件的情况 : 132 and 213

输入 : N = 4, K = 2

输出 : 2

解法的伪代码如下：

If N is 0, Count(0, K) = 0

If K is 0, Count(N, 0) = 1 (Only sorted array)

In general case, 
If we have N number and require K inversion, 
Count(N, K) = Count(N - 1, K) + 
              Count(N – 1, K - 1) + 
              Count(N – 1, K – 2) + 
              .... + 
              Count(N – 1, 0)

其解法思想如下：

如果我们有N个数并希望有K个inversion，并且假设（N-1）个数的所有inversion写在某个地方，那么新数（第N个数，即最大的数）需要被置于（N-1）个数的所有inversion中，在我们的答案中应该加上那些inversion计数变为K后的组合。

简单的说就是将第N个数插入在前N-1个数的所有组合中，将inversion=k的情况相加。
下面给出了各个情况的示意图：
1. 前n-1个已经组成了inversions=k，则第n个只需要插入在最后。

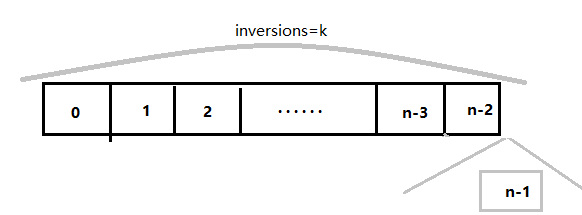
2. 前n-1个已经组成了inversions=k-1，则第n个需要往前插 1 位，让inversions=k。

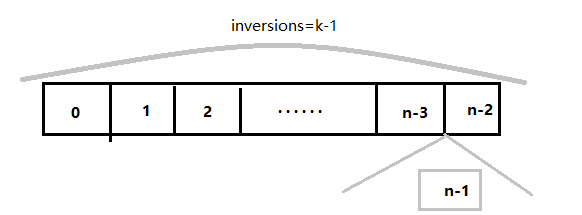
3. 前n-1个已经组成了inversions=k-2，则第n个需要往前插 2 位，让inversions=k。

。
。
。
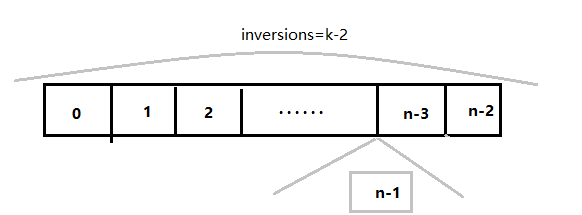
依次类推：

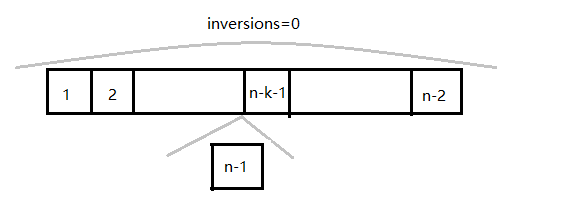
实现代码如下（c++）：

// C++ program to find number of permutation with
// K inversion using Memoization
#include <bits/stdc++.h>
using namespace std;

// Limit on N and K
const int M = 100

// 2D array memo for stopping solving same problem
// again
int memo[M][M];

// method recursively calculates permutation with
// K inversion
int numberOfPermWithKInversion(int N, int K)
{
    //  base cases
    if (N == 0)
        return 0;
    if (K == 0)
        return 1;

    //  if already solved then return result directly
    if (memo[N][K] != 0)
        return memo[N][K];

    // calling recursively all subproblem of
    // permutation size N - 1
    int sum = 0;
    for (int i = 0; i <= K; i++)
    {
        // Call recursively only if total inversion
        // to be made are less than size
        if (i <= N - 1)
            sum += numberOfPermWithKInversion(N-1, K-i);
    }

    //  store result into memo
    memo[N][K] = sum;

    return sum;
}

//  Driver code to test above methods
int main()
{
    int N = 4;
    int K = 2;
    cout << numberOfPermWithKInversion(N, K);
    return 0;
}

Output:

5