机器学习作业5——逻辑回归

最新推荐文章于 2024-07-26 13:24:37 发布

T.HLQ12

最新推荐文章于 2024-07-26 13:24:37 发布

阅读量692

点赞数 14

文章标签：机器学习逻辑回归人工智能

本文链接：https://blog.csdn.net/u013731025/article/details/138943488

版权

一、理论

需求：

首先明确一下需求：我希望有一个模型，往里头输入一些特征值，就能得出是否为一个类别输出，而当这个概率大于0.5，就认为是这个类别，反之不是。所以逻辑回归的名虽然带回归，但是是拿来分类的。

为了实现这个需求，将特征化为值后将样本作为一个个点放入坐标系，我希望找到决策边界，假设特征最多只有两个，决策边界也就是一条线，这条线能够作为分界线，一侧的是一个类别，另一侧是另一个类别（二分类）。

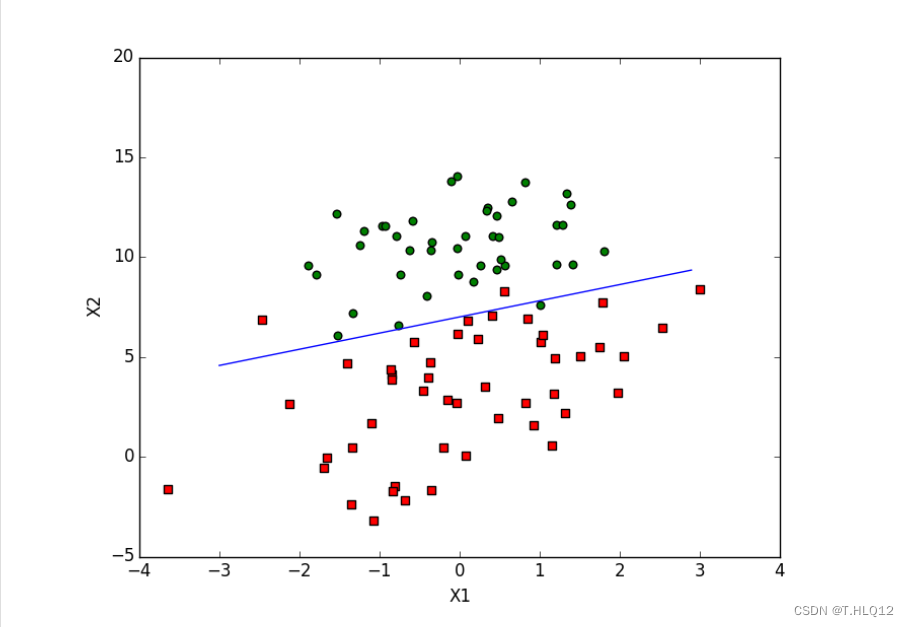
上图的一条线就是想要的决策边界，x1和x2是两个特征。

得到决策边界“z”之后，输入特征后，得到的值域是 $(-\infty, \infty)$ ，不好预测属于哪一类，所以引入sigmoid函数，将决策边界带入其中。

sigmoid函数：

具体为 $h(x) = \frac{1}{1 + e^{-z}}$ ，z是决策边界， $z = w^T x + b$ 。

图像：

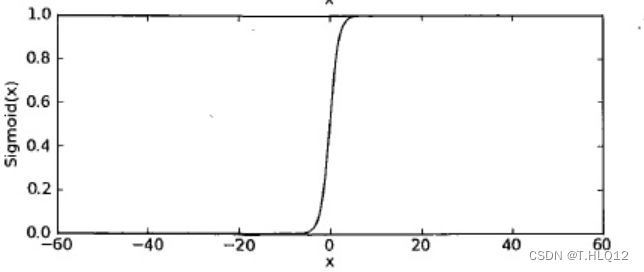
可以看到这个图像的值域只有[0, 1]，也可以保持和原函数一样的单调性，而0~1的值域也方便作为概率来看待，所以这个函数很妙。

现在将这个函数视作样本x作为类别1的概率，那么自然地作为类别2的概率就为 $1-h(z)$

并且当x=0，也就是当想要预测的点落在分类边界，难以预测的时候，值为0.5，也就是预测为两种类型的概率都为0.5，可以理解。

最大似然函数：

最开始是这样，按照分类标签，1~k的是标签为1的，k+1~n的是标签为0的。

$\prod _{i=1}^{i=k}h(x_{i})\prod _{i=k+1}^{n}(1-h(x_{i}))$ .

显然，上式的结果是一个概率的乘积，按照最大似然函数的解释：对于已经出现的样本，我们希望他出现的概率是最大的，所以我们需要最大化这个式子，如何最大化呢？就需要修改里面的参数，使其最大。

在找最大值之前，因为上式需要先对0，1标签分类，实在麻烦，所以可以根据标签只有0和1，写出以下等价式子：

$\prod _{i=1}^{n} h(\mathbf{x}_{i})^{y_{i}}(1-h(\textbf{x}_{i}))^{1-y_{i}}$

又因为是连乘，找最大值麻烦，所以对其取对数，得到：

$L(\textbf{w})=\frac{1}{n}\sum _{i=1}^{n} -y_{i}ln(h(\mathbf{x}_{i}))-(1-y_{i})ln(1-h(\textbf{x}_{i}))$

可以看到上面式子多了个 $\frac{1}{n}$ ，这只是为了防止值过大，所以除个n。

然后因为看到的资料中，多数示范都喜欢乘个-1，使其求的是最小值，所以我们也乘个-1，变成：

$L(w) = -\frac{1}{N} \sum_{i=1}^{N} [y^{(i)} \log(\hat{y}^{(i)}) + (1 - y^{(i)}) \log(1 - \hat{y}^{(i)})]$

接下来开始求上式的最小值。

我们都学过，求最小值可以对其求导，找0点，而事实上找0点复杂度有点高，所以这里选择梯度下降方法。

梯度下降：

梯度下降，就是朝着函数最小值的地方靠近，因为是往最小值走的，所以名为下降。

首先对其的参数w进行求偏导，化简后得到：

$\frac{\partial J(w)}{\partial w} = -\frac{1}{N} \sum_{i=1}^{N} \left( y^{(i)} - \hat{y}^{(i)} \right) x^{(i)}$

其中xi表示第i个特征（因为有n个特征，所以要对每个特征的参数求一次偏导，然后加起来）

然后每次往方向 $\frac{\partial J(w)}{\partial w}$ 走 $\alpha$ 步，迭代更新参数，公式为：

$w_{i}{ }^{k+1} =w_{i}^{k}-\alpha \cdot \frac{\partial J(w)}{\partial w}$

到这里训练的过程就差不多结束了。

ps: 迭代次数和 $\alpha$ 学习率是自己设置的，还有值得说的一点就是，当每次 $w_{i}^{k}$ 更新的值几乎不变，也就是 $w_{i}{ }^{k+1} -w_{i}^{k}$ 小于自己设定的阈值时，可以提前退出迭代循环，不用浪费时间。

总结一下该干什么：

对着已有的权值，不断找最小值就可以了，而每次找最小值，就需要用到 $\frac{\partial J(w)}{\partial w}$ 和 $h(x)$ ，至于损失函数或者最大似然函数，实际上不需要知道他们的值，只需要知道我们正在往最小值靠近就好。所以每次迭代的时候要做的事情就是：1、求偏导，2、参数更新。

当然存在一种情况就是，可能卡在是极小值，或是驻点，而不是最小值的地方。对于这种情况，可以反复调整学习率和最开始初始化的权值，来探索不一样的区间，到最后能找到一个合适的参数即可，不需要过分完美。

假如训练完了，该如何预测呢？

就像开头说的那样，将特征值带入sigmoid函数中计算，根据训练好的参数，计算结果并进行四舍五入，最终得到标签。

二、代码

import numpy as np
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score

from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import StandardScaler
from sklearn.model_selection import train_test_split


class LogisticRegression:

    def __init__(self, learning_rate=0.1, max_iter=1000, tol=1e-6, random_state=None):
        self.learning_rate = learning_rate  #学习率
        self.max_iter = max_iter           #迭代次数
        self.tol = tol                    #收敛阈值
        self.random_state = random_state  #随机种子
        self.theta = None                 #参数

    def sigmoid(self, z):
        return 1 / (1 + np.exp(-z))
    
    #损失函数
    def cost_function(self, X, y, theta):
        h = self.sigmoid(X.dot(theta))
        J = -1 / len(y) * np.sum(y * np.log(h) + (1 - y) * np.log(1 - h))#公式
        return J

    #求偏导
    def gradient(self, X, y, theta):
        h = self.sigmoid(X.dot(theta))
        #print("预测："+repr(h))
        grad = 1 / len(y) * X.T.dot(h - y)#公式
        return grad

    def fit(self, X, y):
        # 训练模型
        if self.random_state:
            np.random.seed(self.random_state)
        self.theta = np.random.randn(X.shape[1])
        for i in range(self.max_iter):
            grad = self.gradient(X, y, self.theta)
            self.theta -= self.learning_rate * grad
            if abs(sum(self.learning_rate*grad)) < self.tol:
                 break
            if i%100 == 0 :
                print("迭代了"+repr(i)+"次，损失函数为："+repr(self.cost_function(X, y, self.theta)))


    def predict(self, X):
        y_pred = np.round(self.sigmoid(X.dot(self.theta)))
        return y_pred
    

iris = load_iris()
X = iris.data
y = (iris.target != 0) * 1  #*1使得bool数组变类型

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)

#特征标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)


print("训练集：")
print(X_train_scaled)
print("测试集：")
print(X_test_scaled)


model = LogisticRegression(learning_rate=0.7, max_iter=0)
model.fit(X_train_scaled, y_train)


y_pred = model.predict(X_test_scaled)



for i in range(len(y_pred)):
    print("预测，正确： "+repr(y_pred[i]) + "   " + repr(y_test[i]))
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
print("准确率:", accuracy)  
print("精确率:", precision)  
print("召回率:", recall)  
print("f1:", f1)

一些解释：

使用鸢尾花数据集来训练，最开始权值不确定，随机一个出来就好，然后就可以开始进行梯度下降了。要干什么上面的第一步说过了，函数照着步骤写即可，不再赘述。

ps：最开始随机权值使用np.random.randn(X.shape[1])，用来生成一个具有标准正态分布（均值为 0，方差为 1）的随机数组，随机的一个好处就是可以探索不一样的区间，避免每次卡在同一个极小值处。

三、结果

当学习率为0.1，迭代500次的时候：

可以看到效果已经十分好了。

接下来是学习率为0.1，迭代次数为50的结果：

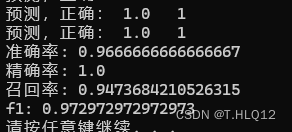
学习率为0.01，迭代次数为50的结果：

学习率为0.001，迭代次数为50的结果：

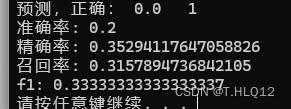
当迭代次数为0的时候，其中一种结果：

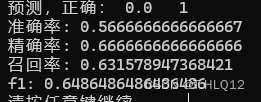
可以看到次数为0，也有一定的效果，说明随机初始参数在迭代次数少的时候对于结果的影响还是很大的。

四、优缺点分析

优点：

实现简单：逻辑回归是一种线性模型，参数可以通过最大似然估计或梯度下降等方法进行求解，实现相对简单。
计算效率高：逻辑回归的计算代价相对较低，适用于处理大规模数据集。
输出结果易解释：逻辑回归通过sigmoid函数将线性回归的结果映射到0到1之间，可以直观地理解为概率值，便于解释和可视化。

缺点：

假设线性关系：逻辑回归假设特征与目标变量之间存在线性关系，当特征之间存在非线性关系时，可能无法很好地拟合数据。
对异常值敏感：逻辑回归对异常值比较敏感，异常值的存在可能会影响模型的性能。
处理多类问题困难：逻辑回归主要用于二分类问题，对于多类问题需要进行适当的扩展。

可以的优化：

梯度下降可以改为：随机梯度下降和小批量梯度下降。
牛顿法：利用损失函数的二阶导数信息，通过迭代更新参数，寻找损失函数的极小值点。牛顿法通常比梯度下降法收敛更快，但计算复杂度较高。
多项式特征: 可以将原始特征进行多项式展开，例如将二次、三次等高阶特征加入到模型中，这样可以使得逻辑回归模型能够拟合非线性关系。
核技巧: 在使用支持向量机时常用的核技巧（如多项式核、高斯核等）也可以应用在逻辑回归中，将低维的输入特征映射到高维空间，从而实现非线性逻辑回归。

学习中遇到的一些问题：

主要还是理论方面需要时间理解，代码方面在明确理论后实现起来不会太难。

最初看到极大似然函数和损失函数的时候，一直弄混，不明确这两是什么关系，还有有些地方写着梯度上升，另一些写着梯度下降，这些相似但不同的概念在刚开始学的时候会使得思绪很凌乱，对比理解一段时间后就慢慢理清楚了。

T.HLQ12

关注

14
点赞
踩
30

收藏

觉得还不错? 一键收藏
2
评论
机器学习作业5——逻辑回归

对着已有的权值，不断找最小值就可以了，而每次找最小值，就需要用到和，至于损失函数或者最大似然函数，实际上不需要知道他们的值，只需要知道我们正在往最小值靠近就好。所以每次迭代的时候要做的事情就是：1、求偏导，2、参数更新。当然存在一种情况就是，可能卡在是极小值，或是驻点，而不是最小值的地方。对于这种情况，可以反复调整学习率和最开始初始化的权值，来探索不一样的区间，到最后能找到一个合适的参数即可，不需要过分完美。假如训练完了，该如何预测呢？
复制链接

扫一扫