一、生成1~n的排列:
这代码的实现使用了递归的方式!唉,但是关于递归的使用还是不够熟练,理解亦不够深入,顾作此文!
还有就是从算法到程序的实现,觉得还是欠缺很多啊!
/*
Date:2014/11/02
By: VID
Function: 在本程序中实现了两个功能。
1、 输入正整数n,按字典序从小到大的顺序输出1~n的所有排列。列如:
Sample Input
3
Sample Output
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
2、手动录入数组(输入的没有重复元素!!),按字典序从小到大的顺序输出该数组的所有排列。(程序中所有标注方式2的。)列如:
Sample Input
3
2 4 6
Sample Output
2 4 6
2 6 4
4 2 6
4 6 2
6 2 4
6 4 2
*/
#include<iostream>
using namespace std;
#define N 500
int P[N],A[N];
// 递归…
void print_pumutation(int n,int* A,int cur)
{
int i,j;
if(cur == n) // cur指的是当前的位置!
{
for(i = 0;i<n;i++) cout<<A[i];
cout<<endl;
}
else for(i = 1;i<=n;i++)// 若为方式2:就要修改为:for(i = 0;i<n;i++)
{
int ok = 1;
for(j = 0;j<cur;j++)
if(A[j] == i) ok = 0;
// 方式2: if(A[j] == P[i]) ok = 0;
if(ok)
{
A[cur] = i;
//方式2: A[cur] = P[i];
print_pumutation(n,A,cur+1);
}
}
}
int main()
{
int n;
while(cin>>n)
{
/*
方式2:
for(int i = 0;i<n;i++)
{
cin>>P[i];
}
*/
memset(A,0,sizeof(A));
print_pumutation(n,A,0);
}
return 0;
}二、生成可重集的排列
注:这里的意思是输入中有重复元素,我们输出的各个排列当然是不会重复的。
例如:Sample Input
3
1 1 2
Sample Output
1 1 2
1 2 1
2 1 1
对于这样的问题:
/*
Date:2014/11/02
By: VID
Attention:
对于这样的问题,只需在上一个程序的基础之上做一些修改,
便可得到输入是重复集的全排列。
->如果想用字典序输出,只需加上一个排序的函数即可。
*/
#include<iostream>
using namespace std;
#define N 500
int P[N],A[N];
// 递归…
void print_pumutation(int n,int P[],int* A,int cur)
{
int i,j;
if(cur == n) // cur指的是当前的位置!
{
for(i = 0;i<n;i++) cout<<A[i];
cout<<endl;
}
else for(i = 0;i<n;i++)
if(!i||P[i]!=P[i-1]) // 这里是为了检查P的第一个元素和所有与第一个元素不相同的元素,
// 只有这个时候,我们才对它进行递归调用!
{
int c1 = 0,c2 = 0;
for(j = 0;j<cur;j++)
if(A[j] == P[i]) c1++; // 在A[0]~A[cur-1]中P[i]出现的次数。
for(j = 0;j<n;j++)
if(P[i] == P[j]) c2++; // 在数组P中P[i]出现的次数。
if(c1<c2)
{
A[cur] = P[i];
print_pumutation(n,P,A,cur+1);
}
}
}
int main()
{
int n;
while(cin>>n)
{
for(int i = 0;i<n;i++)
{
cin>>P[i];
}
memset(A,0,sizeof(A));
print_pumutation(n,P,A,0);
}
return 0;
}
(2)与上面的刚刚相反,下面的程序输出的每一个排列之中的元素是可以重复的,而元素输入是不能有重复的。
例如:Sample Input
2
1 2
Sample Output
1 1
1 2
2 1
/*
Date:2014/11/02
By: VID
Function:
使用规则:要求输入的元素没有重复元素。
结果 :输出有重复元素的全排列!!
*/
#include<iostream>
using namespace std;
#define N 500
int P[N],A[N];
void print_pumutation(int n,int* A,int cur)
{
int i,j;
if(cur == n) // cur指的是当前的位置!
{
for(i = 0;i<n;i++) cout<<A[i];
cout<<endl;
}
else for(i = 0;i<n;i++)
{
A[cur] = P[i];
print_pumutation(n,A,cur+1);
}
}
int main()
{
int n;
while(cin>>n)
{
for(int i = 0;i<n;i++)
{
cin>>P[i];
}
memset(A,0,sizeof(A));
print_pumutation(n,A,0);
}
return 0;
}关于刚刚上面研究的两个问题,还可以使用STL中的库函数next_permutation(生成下一个全排列!)。这个函数可以轻松的解决上面的两个问题。下面举个例子,这个例子来自:点击打开链接
/*
对于这些"lcq", "love", "code", "plmm"字符串按照字典序把他们的全排列输出来。
所以当然,对于字符串都可以输出他们的排列,简单的整形数组就更不在话下,可以很出色的解决
他们的全排列,无论输入是否有重复。
*/
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int main()
{
string word[] = {"lcq", "love", "code", "plmm"};//C++里面带的一个string类
int n = sizeof(word) / sizeof(word[0]);
sort(word, word+n);//排序
do
{
for(int i=0; i<n; ++i)
cout<<word[i]<<" ";
cout<<endl;
}while(next_permutation(word, word+n));
return 0;
}
/***Output********
code lcq love plmm
code lcq plmm love
code love lcq plmm
code love plmm lcq
code plmm lcq love
code plmm love lcq
lcq code love plmm
lcq code plmm love
lcq love code plmm
lcq love plmm code
lcq plmm code love
lcq plmm love code
love code lcq plmm
love code plmm lcq
love lcq code plmm
love lcq plmm code
love plmm code lcq
love plmm lcq code
plmm code lcq love
plmm code love lcq
plmm lcq code love
plmm lcq love code
plmm love code lcq
plmm love lcq code
******************/->接下来是这个神奇的函数:next_permutation的函数内部实现过程(当然也有prev_permutation)。见代码:
#include<iostream>
#include<algorithm>
using namespace std;
template<class BidirectionalIterator>
bool my_next_permutation(BidirectionalIterator first, BidirectionalIterator last)
{
if(first == last)//空区间
return false;
BidirectionalIterator i = first;
if(last == ++i)//只有一个元素
return false;
i = last;//i 指向尾端
--i;
for(;;)
{
BidirectionalIterator ii = i;
--i;
if(*i < *ii)//如果前一个元素小于后一个元素
{
BidirectionalIterator j = last;//令j指向尾端
while(!(*i < *--j));//有尾端往前栈、直到遇上比 *i大的元素
iter_swap(i, j);//交换i,j
reverse(ii, last);//将ii之后的元素全部逆向重排
return true;
}
if(i == first)//进行至最前面了
{
reverse(first, last);//全部逆向重排
return false;
}
}
}
int main()
{
char a[] = {'d', 'c', 'a', 'a'};
int n = sizeof(a) / sizeof(a[0]);
sort(a, a+n);
do
{
for(int i=0; i<n; ++i)
cout<<a[i]<<" ";
cout<<endl;
}while(my_next_permutation(a, a+n));
return 0;
}三、子集生成(!!!下面的内容来自http://blog.csdn.net/luchenqun/article/details/6401954)
Description
从集合{1,2,3,...,n}中选取k个数所组成的所有集和。
Input
输入的两个正整数。第一个数为n(1<=n<=20),第二个数为k,(k<=n),两个数之间用空格隔开。
Output
输出含有k个数的所有不相同的集合,输出集合的序列按照字典序输出,每个集合占一行,集合的相邻两个数字用空格隔开。
Sample Input
3 2
Sample Output
1 2
1 3
2 3
(1)、增量构造法:即:一次选出一个元素放到集合中。
#include<stdio.h>
#include<iostream>
#include<stdlib.h>
using namespace std;
const int MAX = 100;
int cmp(const void *a, const void *b)
{
return *(int*)a - *(int*)b;
}
void fullCombination(int num[], int rcd[], int cur, int begin, int n)
{
int i;
for(i=0; i<cur; ++i)
printf("%d ", rcd[i]);
printf("\n");
for(i=begin; i<n; ++i)
{
rcd[cur] = num[i];
fullCombination(num, rcd, cur+1, i+1, n);
}
}
int main()
{
int num[MAX], rcd[MAX], i, n,a;
cin>>n;
while(1)
{
for(i=0; i<n; ++i)
{
cin>>a;
num[i] = a;
}
qsort(num, n, sizeof(num[0]), cmp);
fullCombination(num, rcd, 0, 0, n);
}
return 0;
}
/*
INPUT
3
3 2 1
OUTPUT
1
1 2
1 2 3
1 3
2
2 3
3
*/
很显然,递归的边界是集合num[]中没有数的时候。
(2)、位向量法:
第二种方法是构造一个位向量B[i],其中当B[i]==1的时候i元素在子集a[]中,B[i]==0时不在子集a[]中。代码如下:
#include<stdio.h>
const int MAX = 100;
void fullCombination(int n, int* B, int cur)
{
if(cur == n)
{
for(int i = 0; i < cur; i++)
{
if(B[i])
printf("%d ", i+1); // 打印当前集合
}
printf("/n");
return;
}
B[cur] = 1; // 选第cur个元素
fullCombination(n, B, cur+1);
B[cur] = 0; // 不选第cur个元素
fullCombination(n, B, cur+1);
}
int main()
{
int B[MAX], n;
while(scanf("%d", &n) != EOF)
fullCombination(n, B, 0);
return 0;
}
/*
INPUT
3
OUTPUT
1 2 3
1 2
1 3
1
2 3
2
3
*/
(三)、二进制法
接下来我要重点介绍的一种方法是利用二进制来表示{1,2,3,……,}的子集S:从右往左用一个整数的二进制表示元素i是不是再集合S中。下面演示了用二进制110110100表示集合{7,6,4,3,1}。
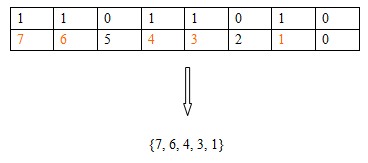
OK,有了这个思想,我们就可以把整数想象为二进制的数,实际上,我们也知道,整数在机器里面都是用0,1表示的,可以这么说,0,1创造了计算机的整个世界。这就是为什么判断一个整数是不是奇数用if(n&1) n为奇数;(奇数用二进制表示末尾一定是1)比用if(1 == n%1) n为奇数;快多了的原因。知道了表示,还要知道怎样操作整数来表示集合,这点发明C语言的人早就为我们想到了。他们分别是&,|, ^.
好了,就看怎样用代码实现吧:
#include<stdio.h>
void fullCombination(int n, int s) // 打印{1, 2, ..., n}的子集S
{
for(int i = 0; i < n; i++)
{
if(s&(1<<i))
printf("%d ", i+1); // 这里利用了C语言“非0值都为真”的规定
}
printf("/n");
}
int main()
{
int n;
while(scanf("%d", &n) != EOF)
{
for(int i = 0; i < (1<<n); i++) // 枚举各子集所对应的编码 0, 1, 2, ..., 2^n-1
fullCombination(n, i);
}
return 0;
}
/*
INPUT
3
OUTPUT
1
2
1 2
3
1 3
2 3
1 2 3
这段代码的效率肯定要比前面两段代码快多了。不过不要得意太早,你输入31试试?代码什么也没输出。这是为什么呢?1~30都能输出他的所有子集,为什么30以后的就不行了……仔细想想int是多少位你就明白了……所以还是应了那句话,出来混的,迟早是要还的,而前面两段代码虽然效率低些,但只要内存足够,原则上是能输出1~UINT_MAX的子集。
我比较喜欢第三段代码。所以把第三段代码稍微修改一下就能完成老师的所提的问题了。修改后的代码如下:
#include<stdio.h>
int numOfOne(int n)//计算n转换为二进制后1的个数
{
int count = 0;
while(n)
{
if(n&1)
count++;
n>>=1;
}
return count;
}
void fullCombination(int n, int s, int k) // 打印{1, 2, ..., n}的子集S
{
int count=0;
for(int i = 0; i < n; i++)
{
if(s&(1<<i) && k==numOfOne(s))//s二进制中1的个数决定了子集s中的元素的个数
{
printf("%d ", i+1); // 这里利用了C语言“非0值都为真”的规定
count++;
}
}
if(k == count)
printf("/n");
}
int main()
{
int n, k;
while(scanf("%d %d", &n, &k) != EOF)
{
for(int i = 0; i < (1<<n); i++) // 枚举各子集所对应的编码 0, 1, 2, ..., 2^n-1
fullCombination(n, i, k);
}
return 0;
}
/****************
4 2
1 2
1 3
2 3
1 4
2 4
3 4
5 3
1 2 3
1 2 4
1 3 4
2 3 4
1 2 5
1 3 5
2 3 5
1 4 5
2 4 5
3 4 5
***************/问题:(因为上面的子集生成的代码都不能解决如果输入的数有相同的这一问题,顾有下面的这一题)
3、如果输入n个数,求着n个数构成的所有子集,不允许输出重复项。如
输入
3
1 1 3
输出
1
1 1
1 1 3
1 3
3
#include <stdio.h>
#define MAX_N 10
int rcl[MAX_N], num[MAX_N], used[MAX_N];
int m,n;
void unrepeat_combination(int index, int p)
{
int i;
for (i=0; i<index; i++)
{
printf("%d", rcl[i]);
if (i<index-1)
{
printf(" ");
}
else
printf("\n");
}
for (i=p; i<n; i++)
{
if (used[i]>0)
{
used[i]--;
rcl[index] = num[i];
unrepeat_combination(index+1, i);
used[i]++;
}
}
}
int read_data()
{
if (scanf("%d", &n)== EOF)
{
return 0;
}
int i, j, val;
m = 0;
for (i=0; i<n; i++)
{
scanf("%d", &val);
for (j=0; j<m; j++)
{
if (val == num[j])
{
used[j]++;
break;
}
}
if (j==m)
{
num[m] = val;
used[m] = 1;
m++;
}
}
return 1;
}
void main()
{
while(read_data())
{
unrepeat_combination(0, 0);
}
}
======================================================================================
总结:关于枚举排列与子集生成的大部分方法都整理出来了,借鉴了很多资料。希望能给自己梳理一下整个思路,能有所收获!
另外:
1、输入一个数组a[],里面有n(1<=n<=1000)个数,给出数组a[]所有数字的一个全排列,求他按照字典排序,这个全排列是所有排列中的第几个。比如a[5] = {1, 1, 4, 5, 8};1 4 1 5 8是该全排列的第8个。
2、如果不晓得对全排列掌握得怎么样,请到POJ上提交你的代码,注意,请不要使用next_permutation();题目的链接为:
http://poj.org/problem?id=1731
http://poj.org/problem?id=1256
http://poj.org/problem?id=1833
http://poj.org/problem?id=1318
http://poj.org/problem?id=1146
如果你能不使用next_permutation()把这5个题目AC,那么,估计以后面试的时候全排列应该没问题。等不用next_permutation()把那五个题目AC之后,再用next_permutation()爽一把吧。
3、同时考虑如何生成一个规定个数的子集,且子集里的元素可以重复出现。
例如:
INPUT
6
1 2 4 6 7 9
OUTPUT
……
1 1 1 1 2 2
1 1 1 1 1 2
……
像是这种,输入的数据没有重复的,但是每个生成的小的排列内部,比如1 就可以重复使用多次,而且这个输出序列元素个数是这输入元素的个数决定的!
另外还有关于递归的过程梳理,一定要整理出一片博客来!






















 6664
6664

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








