opencv2矩阵操作

最新推荐文章于 2024-06-14 00:05:22 发布

叶落西湘

最新推荐文章于 2024-06-14 00:05:22 发布

阅读量2.1k

点赞数

分类专栏： opencv与机器视觉文章标签： opencv 矩阵操作

opencv与机器视觉专栏收录该内容

14 篇文章 0 订阅

订阅专栏

文章转载自新浪博客：http://blog.sina.com.cn/s/blog_7908e1290101i97z.html
综述:
- OpenCV有针对矩阵操作的C语言函数. 许多其他方法提供了更加方便的C++接口，其效率与OpenCV一样.
- OpenCV将向量作为1维矩阵处理.
- 矩阵按行存储，每行有4字节的校整.
- //由于opencv的矩阵式一位数组或者一位指针，所以我们只能利用opencv的函数对矩阵元素进行操作（当然这样也是最安全的做法，- -！太不习惯了）

分配矩阵空间:

CvMat* cvCreateMat(int rows, int cols, int type);

 

type: 矩阵元素类型. 格式为CV_(S|U|F)C. 例如: CV_8UC1 表示8位无符号单通道矩阵, CV_32SC2表示32位有符号双通道矩阵.

例程: CvMat* M = cvCreateMat(4,4,CV_32FC1)//这个函数用来初始化Mat，不初始化虽然是会报warrying，但是运行时会报错，由于Mat和IplImage的类型不太一样，所以做两者之间转换的时候想改变数据类型很难（大概可以先转换矩阵类型，再转换数据类型，这就麻烦了，还没找到好方法），还需要注意这个分配空间并不管理数据的初始化，最好利用cvSet对数据进行初始化。

释放矩阵空间:

CvMat* M = cvCreateMat(4,4,CV_32FC1); cvReleaseMat(&M);//这个别忘了用就是了

复制矩阵:

CvMat* M1 = cvCreateMat(4,4,CV_32FC1);

CvMat* M2;

M2=cvCloneMat(M1);

初始化矩阵:

double a[] = { 1, 2, 3, 4,

5, 6, 7, 8, 9, 10, 11, 12 };

 

CvMat Ma=cvMat(3, 4, CV_64FC1, a);

另一种方法:

CvMat Ma; cvInitMatHeader(&Ma, 3, 4, CV_64FC1, a);

初始化矩阵为单位阵:

 CvMat* M = cvCreateMat(4,4,CV_32FC1); cvSetIdentity(M); // 这里似乎有问题。

 //这个函数可以初始化对角线上的元素，这个是单位阵，不是所有元素都赋1，这个函数需要第二个函数，虽然有默认值，但是这个变量和我之前的理解有点不对，也没有实验，贴个原型吧：

 void cvSetIdentity( CvArr* mat, CvScalar value=cvRealScalar(1) );这里的cvRealScalar（1）是个强制类型转换。

存取矩阵元素
假设需要存取一个2维浮点矩阵的第(i,j)个元素.
间接存取矩阵元素:

cvmSet(M,i,j,2.0); // Set M(i,j) t = cvmGet(M,i,j); // Get M(i,j)

直接存取，假设使用4-字节校正:

CvMat* M = cvCreateMat(4,4,CV_32FC1); int n = M->cols; float *data = M->data.fl; data[i*n+j] = 3.0;

直接存取，校正字节任意:

CvMat* M = cvCreateMat(4,4,CV_32FC1);

int step = M->step/sizeof(float);

float *data = M->data.fl;//这个也是Mat和IplImage的区别，Mat的data是union类型，里面是五个不同类型的指针，根据你存储的类型选择相同类型的指针；而IplImage的imagedata就直接存储数据了。

 

(data+i*step)[j] = 3.0;

直接存取一个初始化的矩阵元素:

double a[16]; CvMat Ma = cvMat(3, 4, CV_64FC1, a); a[i*4+j] = 2.0; // Ma(i,j)=2.0;

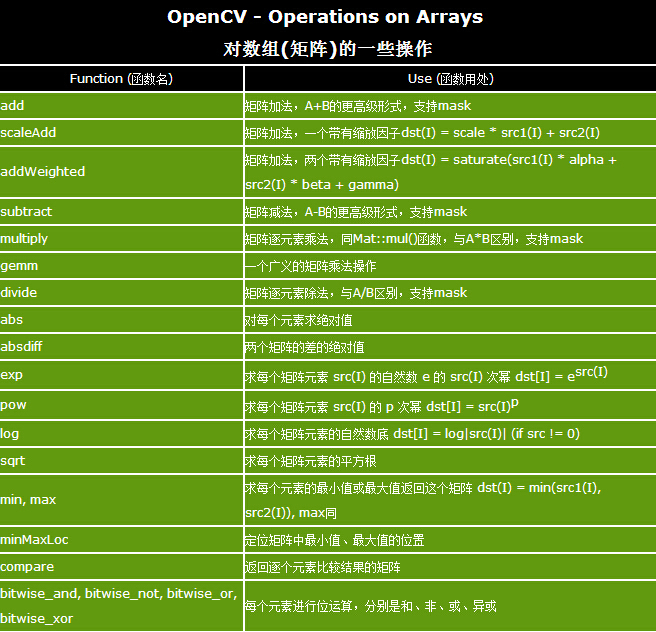
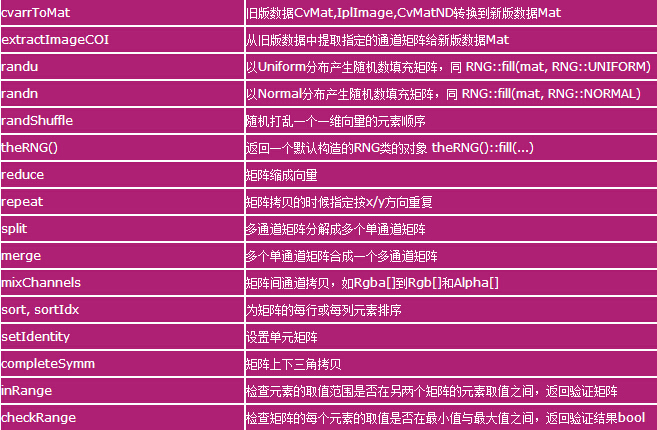
矩阵/向量操作

矩阵-矩阵操作:

CvMat *Ma, *Mb, *Mc; cvAdd(Ma, Mb, Mc); // Ma+Mb -> Mc cvSub(Ma, Mb, Mc); // Ma-Mb -> Mc cvMatMul(Ma, Mb, Mc); // Ma*Mb -> Mc//从前几天看到的一些技巧，我感觉这个几个函数不是很好，没有返回值，不能嵌套调用，想完成三个矩阵的相乘，还需要临时变量，比如恢复SVD的时候。

按元素的矩阵操作:

CvMat *Ma, *Mb, *Mc; cvMul(Ma, Mb, Mc); // Ma.*Mb -> Mc cvDiv(Ma, Mb, Mc); // Ma./Mb -> Mc cvAddS(Ma, cvScalar(-10.0), Mc); // Ma.-10 -> Mc

向量乘积:

double va[] = {1, 2, 3}; double vb[] = {0, 0, 1}; double vc[3];

CvMat Va=cvMat(3, 1, CV_64FC1, va); CvMat Vb=cvMat(3, 1, CV_64FC1, vb); CvMat Vc=cvMat(3, 1, CV_64FC1, vc);

double res=cvDotProduct(&Va,&Vb); // 点乘: Va . Vb -> res cvCrossProduct(&Va, &Vb, &Vc); // 向量积: Va x Vb -> Vc end{verbatim}

注意 Va, Vb, Vc 在向量积中向量元素个数须相同.

单矩阵操作:

CvMat *Ma, *Mb; cvTranspose(Ma, Mb); // transpose(Ma) -> Mb (不能对自身进行转置) CvScalar t = cvTrace(Ma); // trace(Ma) -> t.val[0] double d = cvDet(Ma); // det(Ma) -> d cvInvert(Ma, Mb); // inv(Ma) -> Mb

非齐次线性系统求解:

CvMat* A = cvCreateMat(3,3,CV_32FC1); CvMat* x = cvCreateMat(3,1,CV_32FC1); CvMat* b = cvCreateMat(3,1,CV_32FC1); cvSolve(&A, &b, &x); // solve (Ax=b) for x

特征值分析(针对对称矩阵):

CvMat* A = cvCreateMat(3,3,CV_32FC1); CvMat* E = cvCreateMat(3,3,CV_32FC1); CvMat* l = cvCreateMat(3,1,CV_32FC1); cvEigenVV(&A, &E, &l); // l = A的特征值 (降序排列)

// E = 对应的特征向量 (每行)

奇异值分解SVD:
```
CvMat* A = cvCreateMat(3,3,CV_32FC1); CvMat* U = cvCreateMat(3,3,CV_32FC1); CvMat* D = cvCreateMat(3,3,CV_32FC1); CvMat* V = cvCreateMat(3,3,CV_32FC1); cvSVD(A, D, U, V, CV_SVD_U_T|CV_SVD_V_T); // A = U D V^T
```
标号使得 U 和 V 返回时被转置(若没有转置标号，则有问题不成功!!!).//这个函数解释比较少，首先这个函数不能接受IplImage类型的输入变量，其次必须是浮点型，原文中这个问题，我没有遇到，我使用时最后一个参数用的是默认值0。

自己遇到的问题：

1，首先是初始化的问题，opencv提供了初始化Mat和初始化MatHead两种方法，文档中介绍都不分配内存存储数据，但实际上cvCreateMat这个函数是分配空间的，类推IplImage也是这样。不初始化会在运行时报错。

2，为了调用SVD函数，我要用到很多Mat类型的数据，而且要从IplImage转化为Mat，这里可以选择两个函数，一个是cvGetImage，一个是cvConvert。cvGetImage会将输入数据的文件头一并复制，不符合我的要求，我的输入是IPL_DEPTH_8U ，要转化的矩阵是CV_32FC1，第二个函数不会复制文件头。另外要注意，Mat类型中的type包含很多信息，不光有矩阵的数据类型，不要尝试在矩阵复制后，更改type达到上面的目的。更改type会导致release不成功。

3，opencv不支持不同大小的矩阵相加，我又初始化一个载体大小的图像，将水印的奇异值矩阵复制过去，这是我程序为数不多的几次自己编写的程序块，注意更改单个矩阵值的函数是cvmSet和cvmGet。不要自己找啊。

4，cvCreateMat函数并不会对数据进行初始化，最好继续用cvSet对数据进行初始化。

目标

我们有多种方法可以获得从现实世界的数字图像：数码相机、扫描仪、计算机体层摄影或磁共振成像就是其中的几种。在每种情况下我们（人类）看到了什么是图像。但是，转换图像到我们的数字设备时我们的记录是图像的每个点的数值。

例如在上图中你可以看到车的镜子只是一个包含所有强度值的像素点矩阵。现在，我们如何获取和存储像素值可能根据最适合我们的需要而变化，最终可能减少计算机世界内的所有图像数值矩阵和一些其他的信息的描述基质本身。OpenCV 是一个计算机视觉库，其主要的工作是处理和操作，进一步了解这些信息。因此，你需要学习和开始熟悉它的第一件事是理解OpenCV 是如何存储和处理图像。

Mat

OpenCV 自 2001 年出现以来。在那些日子里库是围绕C接口构建的。在那些日子里，他们使用名为IplImage C 的结构在内存中存储图像。这是您将在大多数较旧的教程和教材中看到的那个。使用这个结构的问题是将 C 语言的所有负面效果都摆到了桌面上。最大的问题是手动管理。它是建立在用户来负责处理内存分配和解除分配的假设之上的。当程序规模较小时，这是没有问题的，一旦代码基开始变得越来越大它将会越来越挣扎着处理所有这一切而不是着眼于实际解决自己的开发目标。

幸运的是 c + + 出现了，并引入了类的概念，使得为用户开辟另一条路成为可能：

自动内存管理（或多或少）。好消息是，c + +，如果完全兼容 C 所以进行更改时没有兼容性问题产生。因此， OpenCV其2.0 版本引入一个新的c + + 接口，通过利用这些优点将为你的工作提供新的方法。某种程度上，在其中您不需要拨弄内存管理让你的代码简洁（写得更少，实现的更多）。C + + 接口的唯一主要缺点在于，目前许多嵌入式的开发系统支持仅 C.因此，除非您的目标是这一平台，否则就没有理由再使用旧的方法（除非你是个受虐狂程序员和喜欢自讨苦吃）。

你需要知道的关于Mat的第一件事是你不再需要手动分配其大小并且当你不需要它的时候你不再需要手动释放它。虽然这样做仍然是可能的，大多数 OpenCV 函数将手动分配其输出数据。还有一个额外的好处是如果传递一个已存在Mat对象，它已经为矩阵分配所需的空间，这段空间将被重用。也就是说我们在任何时候只使用与我们执行任务时所必须多的内存一样多的内存。

Mat本质上是由两个数据部分组成的类：（包含信息有矩阵的大小，用于存储的方法，矩阵存储的地址等）的矩阵头和一个指针，指向包含了像素值的矩阵（可根据选择用于存储的方法采用任何维度存储数据）。矩阵头部的大小是恒定的。然而，矩阵本身的大小因图像的不同而不同，通常是较大的数量级。因此，当你在您的程序中传递图像并在有些时候创建图像副本您需要花费很大的代价生成图像矩阵本身，而不是图像的头部。OpenCV 是图像处理库，它包含大量的图像处理函数。若要解决的计算挑战，最终大部分时间你会使用库中的多个函数。由于这一原因图像传给库中的函数是一种常见的做法。我们不应忘记我们正在谈论往往是计算量相当大的图像处理算法。我们想要做的最后一件事是通过制作不必要的可能很大的图像的拷贝进一步降低您的程序的速度。

为了解决这一问题 OpenCV 使用引用计数系统。其思想是Mat的每个对象具有其自己的头，但可能他们通过让他们矩阵指针指向同一地址的两个实例之间共享该矩阵。此外，拷贝运算符将只能复制矩阵头部，也还将复制指针到大型矩阵，但不是矩阵本身。

Mat A, C; //仅创建了头部
A = imread(argv[1], CV_LOAD_IMAGE_COLOR); //在此我们知道使用的方法（分配矩阵）
Mat B(A); //使用拷贝构造函数
C = A; //赋值运算符

复制代码

上文中的所有对象，以相同的单个数据矩阵的结束点。他们头不同，但是使用的其中任何一个对矩阵进行任何修改，也将影响所有其他的。在实践中的不同对象只是提供相同的底层数据不同的访问方法，然而，它们的头部是不同的。真正有趣的部分是您可以创建仅指向完整数据的一小部分的头。例如，要在图像中创建兴趣区域 ( ROI) 您只需创建一个新头设置新边界：

Mat D (A, Rect(10, 10, 100, 100) ); // 用矩形界定Mat E = A(Range:all(), Range(1,3)); // 用行和列来界定

复制代码

现在，你可能会问是否矩阵的本身可以属于多个Mat对象在不再需要时负责清理数据。简短的回答是：最后一个使用它的对象。这对于使用引用计数的机制，每当有人复制Mat对象的头，矩阵的计数器被增加。每当一个头被清除，此计数器被下调。当该计数器变为零，矩阵也就被释放了。因为有时会仍然也要复制矩阵的本身，存在着 clone() 或 copyTo() 函数。

Mat F = A.clone();Mat G;A.copyTo(G);

复制代码

现在 modifyingForGwill 不会影响由 theMatheader 指出的矩阵。你要记得从所有的是：

• 输出图像分配 OpenCV 功能是自动（除非另行指定，否则）。

• 用c + + OpenCV的接口就无需考虑内存释放。

• 赋值运算符和复制构造函数（构造函数）只复制头。

• 使用clone () 或copyTo () 函数将复制的图像的基础矩阵。

存储方法

这是关于你是如何存储的像素值。您可以选择的颜色空间和使用的数据类型。色彩空间是指我们如何结合为了代码指定的颜色的颜色分量。最简单的是灰色的规模。在这里我们所掌握的颜色是黑色和白色。组合的这些让我们能创造很多的灰度级。

对于彩色的方法，我们有很多方法可供选择。不过，每一就是将他们拆解成三个或四个基本组成部分，这些部分就会组合给所有其他的方法。最受欢迎的这一个 RGB，主要是因为这也是我们的眼睛如何建立中我们的眼睛的颜色。其基准的颜色是红、绿、蓝。编写代码的一种颜色的透明度有时第四个元素：添加 alpha (A)。但是，它们很多颜色系统每个具有自身的优势：

• RGB 是最常见的是我们的眼睛使用类似的事情，我们显示系统还撰写使用这些颜色。

· 单纯疱疹和合肥分解颜色到他们的色相、饱和度和亮度值/组件，这是我们来描述颜色更自然的方式。您使用，例如可驳回的最后一个组件，使你不那么明智的输入图像的光照条件的算法。

• YCrCb 使用流行的 JPEG 图像格式。

• CIE L *b*a 是均匀颜色空间，它是非常方便的如果您需要测量给定的颜色，以另一种颜色的距离。

现在，每个建筑构件都自己有效的域。这会导致使用的数据类型。我们如何存储组件的定义只是如何精细的控制，我们已于其域。最小的数据类型可能是 char 类型，这意味着一个字节或 8 位。这可能是有符号（值-127 到 + 127）或无符号（以便可以存储从 0 到 255 之间的值）。虽然这三个组件的情况下已经给 16 万可能的颜色来表示（如 RGB 的情况下）我们可能通过使用浮点数（4 字节 = 32 位）或double（8 字节 = 64 位）数据类型的每个组件获得甚至更精细的控制。然而，请记住增加组件的大小也会增加在内存中的整张图片的大小。

显式创建Mat对象

在Load, Modify and Save an Image 教程中，你已经可以看到如何使用readWriteImageVideo： 'imwrite() <imwrite>' 函数将一个矩阵写到一个图像文件中。然而，出于调试目的显示的实际值就方便得多。您可以实现此通过Mat的 <<运算符。不过，请注意这仅适用于二维矩阵。

虽然Mat是一个伟大的图像容器类，它也是一般矩阵类。因此，利用Mat创建和操作多维矩阵是可能的。您可以通过多种方式创建Mat的对象：

• Mat()构造函数

Mat M(2,2, CV_8UC3, Scalar(0,0,255));

cout << "M = " << endl << " " << M << endl << endl;

对于二维的和多通道的图像，我们首先定义它们的大小：按行和列计数。

然后我们需要指定的数据类型，用于存储元素和每个矩阵点通道的数量。为此，我们根据以下的约定可以作出多个定义：

CV_ [每一项的位数] [有符号或无符号] [类型前缀] C [通道数]

例如，CV_8UC3 意味着我们使用那些长的 8 位无符号的 char 类型和每个像素都有三个项目的这三个通道的形成。这是预定义的四个通道数字。Scalar 是四个元素短向量。指定此和可以初始化所有矩阵点与自定义的值。但是如果你需要更多您可以创建与上部宏和频道号码放在括号中，您可以看到下面的类型。

使用 C\C++ 数组和通过构造函数来初始化

int sz[3] = {2,2,2};Mat L(3,sz,CV_8UC(1),Scalar::all(0));

复制代码

上例为我们展示了如何创建一个二维以上的矩阵。首先指定其维度数，然后传入一个包含了尺寸每个维度信息的指针，其他都保持不变。

•为一个已经存在的IplImage创建一个头：

IplImage* img = cvLoadImage("greatwave.png", 1);

Mat mtx(img); // 转换 IplImage*-> Mat

• Create()函数:

M.create(4,4, CV_8UC(2));

cout << "M = "<< endl << " " << M << endl << endl;

你不能通过这个构造来初始化矩阵中的数值。它只会在新的居住尺寸与旧的矩阵尺寸不合时重新分配矩阵的数据空间。

• MATLAB风格的初始化函数：zeros()， ones()，

：eyes().指定使用的尺寸和数据类型

Mat E = Mat::eye(4, 4, CV_64F);cout << "E = " << endl << " " << E << endl << endl;Mat O = Mat::ones(2, 2, CV_32F);cout << "O = " << endl << " " << O << endl << endl;Mat Z = Mat::zeros(3,3, CV_8UC1);cout << "Z = " << endl << " " << Z << endl << endl;

复制代码

•对于小的矩阵来说你可以使用逗号隔开的初始化函数：

Mat C = (Mat_<double>(3,3) << 0, -1, 0, -1, 5, -1, 0, -1, 0);

cout << "C = " << endl << " " << C << endl << endl;

•为一个已有的Mat对象创建一个新的头然后clone()或者copyTo()这个头.

Mat RowClone = C.row(1).clone();

cout << "RowClone = " << endl << " " << RowClone << endl << endl;

打印格式

注意：你可以通过用randu()函数产生的随机值来填充矩阵。你需要给定一个上限和下限来确保随机值在你期望的范围内：

Mat R = Mat(3, 2, CV_8UC3);

randu(R, Scalar::all(0), Scalar::all(255));

在上一个例子中你可以看到默认的格式选项。尽管如此，OpenCV允许你在符合以下规则的同时格式化你的输出：

• 默认

cout << "R (default) = " << endl << R << endl << endl;

• Python

cout << "R (python) = " << endl << format(R,"python") << endl << endl;

• Comma separated values (CSV)

cout << "R (csv) = " << endl << format(R,"csv" ) << endl << endl;

• Numpy

cout << "R (numpy) = " << endl << format(R,"numpy" ) << endl << endl;

• C

cout << "R (c) = " << endl << format(R,"C" ) << endl << endl;

打印出其它常见数据项

OpenCV 通过<<操作符也为其他常用OpenCV数据结构提供打印输出的支持，如：

• 2D 点

Point2f P(5, 1);

cout << "Point (2D) = " << P << endl << endl;

• 3D 点

Point3f P3f(2, 6, 7);

cout << "Point (3D) = " << P3f << endl << endl;

• std::vector通过 cv::Mat

vector<float> v;

v.push_back( (float)CV_PI); v.push_back(2); v.push_back(3.01f);

cout << "Vector of floats via Mat = " << Mat(v) << endl << endl;

•点的std::vector

vector<Point2f> vPoints(20);

for (size_t E = 0; E < vPoints.size(); ++E)

vPoints[E] = Point2f((float)(E*5), (float)(E % 7));

cout << "A vector of 2D Points = " << vPoints << endl << endl;

这里大多数的例程都是在一个小控制台程序里运行。你可以在这里下载或是在cpp示例文件夹下找到。

你可以在YouTube.上找到一个快速的实例演示

Mat::~Mat

Mat的析构函数。

C++: Mat::~Mat()

析构函数调用Mat::release()。

Mat::operator =

提供矩阵赋值操作。

C++: Mat& Mat::operator=(const Mat& m)

C++: Mat& Mat::operator=(const MatExpr_Base& expr)

C++: Mat& Mat::operator=(const Scalar& s)

参数：

m – 被赋值的右侧的矩阵。矩阵的赋值是一个复杂度为O(1) 的操作。这就意味着没有数据段复制并且有数量的递增两矩阵将使用同一引用计数器。在给矩阵赋新数据之前先由Mat::release()释放引用。

expr –被赋值的矩阵表达式对象。作为第一种赋值方式的逆操作第二种形式可以被重新用到具有适当大小和尺寸的已分配空间的矩阵上以适应表达式的结果。矩阵表达式扩展得到的实函数将自动处理这个分配过程。例如：

C=A+B 扩展成add(A, B, C) , andadd() 要当心C重新分配数据的操作。.

s – 标量赋值给每一个矩阵元，矩阵的大小和类型将不会改变。有现成的赋值运算符。由于他们各不相同请阅读运算符参数说明。

Mat::operator MatExpr

提供一种Mat-to-MatExpr转换运算符

C++: Mat::operator MatExpr_<Mat, Mat>() const

转换运算符不能显示调用而是由矩阵表达式引擎（Matrix Expression engine）内部调用The cast operator should not be called explicitly. It is used internally by the Matrix Expressions engine.

Mat::row

创建一个指定行数的矩阵头。.

C++: Mat Mat::row(int i) const

参数：

i – 一个0基的行索引.

该方法创建一个具有指定了行数的新矩阵头的矩阵并返回它。这是一个复杂度为O(1) 的操作，无须考虑矩阵的尺寸。新矩阵和原矩阵共享一份基础数据。这是一个典型基本矩阵处理操作的例子, axpy是LU和许多其它算法都使用的一个函数

inline void matrix_axpy(Mat& A, int i, int j, double alpha)

{

A.row(i) += A.row(j)*alpha;

}

Note：在当前实现中，下面的代码不会无法按预期的效果工作：

Mat A ;

...

A.row(i) = A.row(j) ；/ /不起作用

发生这种情况是因为 A.row(i) 形成临时矩阵头进一步分配给另一个矩阵头。请记住，每个操作复杂度为O（1），即没有复制任何数据。因此，如果你预期第 j行被复制到第 i行，那么上述赋值不成立。要做到这一点，应该把这种简单的赋值转换到表达式中或使用 Mat::copyTo() 方法：

Mat A ;

...

/ / 可行，但看上去有点目的不明确。

A.row(i) = A.row(j) + 0;

/ / 这是有点儿长，但这是推荐的方法。

A.row(j).copyTo(A.row(i)) ;

Mat::col

创建一个具有指定了矩阵头中列数这个参数的矩阵

C++: Mat Mat::col(int j) const

参数：

j –一个0基（从0开始）的列索引

该方法创建一个具有指定了矩阵头中列数这个参数的新矩阵并作为函数返回值。这是一种复杂度为O(1)的操作，不用考虑矩阵的尺寸大小。新矩阵和原始矩阵共享一份基础数据。参看Mat::row()说明信息。

Mat::rowRange

为指定的行span创建一个新的矩阵头。

C++: Mat Mat::rowRange(int startrow, int endrow) const

C++: Mat Mat::rowRange(const Range& r) const

参数：

startrow – 一个包容性的0基（从0开始）的行span起始索引.。

endrow – 一个0基的独占性的行span.终止索引。

r – Range 结构包含着起始和终止的索引值。该方法给矩阵指定的行span创建了新的头。与Mat::row() 和 Mat::col()相类似这是一个复杂度为O(1)的操作。

Mat::colRange

为指定的行span创建一个矩阵头。

C++: Mat Mat::colRange(int startcol, int endcol) const

C++: Mat Mat::colRange(const Range& r) const

参数：

startcol – 一个包容性的0基（从0开始）的span列起始索引。

endcol –一个0基的独占性的列span.终止索引。

r –Range 结构包含着起始和终止的索引值。该方法给矩阵指定的列span创建了新的头。与Mat::row() 和 Mat::col()相类似这是一个复杂度为O(1)的操作。

Mat::diag

提取或创建矩阵对角线。

C++: Mat Mat::diag(int d) const

C++: static Mat Mat::diag(const Mat& matD)

参数：

d – 对角线的索引值，可以是以下的值：

– d=0 是主对角线

– d>0表示下半部的对角线。例如：d=1对角线是紧挨着住对角线并位于矩阵下方。

– d<0表示来自矩阵上半部的对角线。例如：d= 1表示对角线被设置在对角线的上方并紧挨着。

matD – 单列用于形成矩阵对角线的列。

该方法为指定的矩阵创建一个新的头。然后新矩阵被分割为单独的列矩阵。类似于Mat::row() 和Mat::col() ,它是复杂度为O(1)操作。

Mat::clone

创建一个数组及其基础数据的完整副本。

C++: Mat Mat::clone() const

该方法创建了一个完整的数组副本。原始的step[]不会被考虑在内的。因此数组的副本是一占用total（）*elemSize（）字节的连续阵列。

Mat::copyTo

把矩阵复制到另一个矩阵中。

C++: void Mat::copyTo(OutputArray m) const

C++: void Mat::copyTo(OutputArray m, InputArray mask) const

参数：

m – 目标矩阵。如果它的尺寸和类型不正确，在操作之前会重新分配。

mask – 操作掩码。它的非零元素表示矩阵中某个要被复制。

该方法把矩阵的复制到另一个新的矩阵中在复制之前该方法会调用

m.create(this->size(), this->type);

因此，目标矩阵会在必要的情况下重新分配

尽管m.copyTo(m) works ﬂawlessly,该函数并不处理源矩阵和目标矩阵之间有重叠的部分的情况。当操作掩码指定以及上述的Mat::create重新分配矩阵，新分配的矩阵在数据复制到里面之前全都被初始化为０。

Mat::convertTo

在缩放或不缩放的情况下转换为另一种数据类型。

C++:

void Mat::convertTo(OutputArray m,int rtype,double alpha=1,double beta=0)const

参数：

m – 目标矩阵。如果它的尺寸和类型不正确，在操作之前会重新分配。

rtype – 要求是目标矩阵的类型，或者在当前通道数与源矩阵通道数相同的情况下的depth。如果rtype 为负，目标矩阵与源矩阵类型相同。

beta – 可选的delta加到缩放值中去。

该方法将源像素值转化为目标类型saturate_cast<> 要放在最后以避免溢出

m( x;y) = saturate_cast < rType > ( α*( *this)( x;y) +β)

Mat::assignTo

提供了一个convertTo的功能形式。

C++: void Mat::assignTo(Mat& m, int type=-1 ) const

Parameters

m – 目标阵列。

type – 要求是目标阵列depth或－１（如果阵列的类型和源矩阵类型相同）

这是一个 internally 使用的由 Matrix Expressions引擎调用的方法。

Mat::setTo

将阵列中所有的或部分的元素设置为指定的值。

C++: Mat& Mat::setTo(const Scalar& s, InputArray mask=noArray())

参数：

s – 把标量赋给阵列并转化到阵列的实际类型。

mask – 与 *this尺寸相同的操作掩码。这是Mat::operator=(const Scalar& s)运算符的一个高级变量。

Mat::reshape

在无需复制数据的前提下改变2D矩阵的形状和通道数或其中之一。

C++: Mat Mat::reshape(int cn, int rows=0) const

参数：

cn – 新的通道数。若cn=0，那么通道数就保持不变。

rows –新的行数。若rows = 0, 那么行数保持不变。

该方法为*this元素创建新的矩阵头。这新的矩阵头尺寸和通道数或其中之一发生改变，在以下的情况任意组合都是有可能的：

ü 新的矩阵没有新增或减少元素。通常，rows*cols*channels()在转换过程中保持一致。.

ü 无数据的复制。也就是说，这是一个复杂度为 O(1)的操作。通常，如果该操作改变行数或透过其他方式改变元素行索引，那么矩阵必定是连续的。参见Mat::isContinuous()。

例如，有一存储了STL向量的三维点集，你想用3xN的矩阵来完成下面的操作：

std::vector<Point3f> vec;

...

Mat pointMat = Mat(vec). //把向量转化成Mat, 复杂度为O(1)的运算

reshape(1). // 从Nx1的3通道矩阵得出Nx3 的单通道矩阵

//同样是复杂度为O(1)的运算

t(); // 最后转置Nx3 的矩阵

//这个过程要复制所有的元素

Mat::t

转置矩阵。.

C++: MatExpr Mat::t() const

该方法通过矩阵表达式（matrix expression）实现矩阵的转置The method performs matrix transposition by means of matrix expressions. 它并未真正完成了转置但却返回一个临时的可以进一步用在更复杂的矩阵表达式中或赋给一个矩阵的转置矩阵对象：

Mat A1 = A + Mat::eye(A.size(), A.type)*lambda;

Mat C = A1.t()*A1; //计算(A + lambda*I)^t * (A + lamda*I).

Mat::inv

反转矩阵

C++: MatExpr Mat::inv(int method=DECOMP_LU) const

参数:

method – 反转矩阵的方法。有以下几种可能的值：

– DECOMP_LU是 LU 分解一定不能是单数的。

– DECOMP_CHOLESKY 是 Cholesky LLT只适用于对称正矩阵的分解。该类型在处理大的矩阵时的速度是LU的两倍左右。

– DECOMP_SVD是 SVD 分解。如果矩阵是单数或甚至不是2维，函数就会计算伪反转矩阵。

该方法执行矩阵的反转矩阵表达。这意味着该方法返回一个临时矩阵反转对象并可进一步用于更复杂的矩阵表达式的中或分配给一个矩阵。

Mat::mul

执行两个矩阵按元素相乘或这两个矩阵的除法。

C++: MatExpr Mat::mul(InputArray m, double scale=1) const

参数：

m – 与*this具有相同类型和大小的矩阵,或矩阵表达式。

scale – 可选缩放系数。

该方法返回一个用可选的缩放比率编码了每个元素的数组乘法的临时的对象。注意：这不是一个对应“*”运算符的简单的矩阵乘法。.

例：:

Mat C = A.mul(5/B); // 等价于divide(A, B, C, 5)

Mat::cross

计算3元素向量的一个叉乘积。

C++: Mat Mat::cross(InputArray m) const

参数：

m –另一个叉乘操作对象。

该方法计算了两个３元素向量的叉乘的积被操作向量必须是３元素浮点型的具有相同形状和尺寸的向量。结果也是一语被操作对象的具有相同形状和大小的浮点型３元素向量。

Mat::dot

计算两向量的点乘。

C++: double Mat::dot(InputArray m) const

参数：

m –另一个点积操作对象。

方法计算两个矩阵的点积。如果矩阵不单列或单行的向量，用顶部到底部从左到右扫描次序将它们视为 1 D向量。这些向量必须具有相同的大小和类型。如果矩阵有多个通道，从所有通道得到的点积会被加在一起。

Mat::zeros

返回指定的大小和类型的零数组。

C++: static MatExpr Mat::zeros(int rows, int cols, int type)

C++: static MatExpr Mat::zeros(Size size, int type)

C++: static MatExpr Mat::zeros(int ndims, const int* sizes, int type)

参数

ndims – 数组的维数。

rows–行数。

cols –列数。

size–替代矩阵大小规格Size(cols, rows)的方法。

sizes– 指定数组的形状的整数数组。

type– 创建的矩阵的类型。

该方法返回一个 Matlab 式的零数组初始值设定项。它可以用于快速形成一个常数数组作为函数参数，作为矩阵的表达式或矩阵初始值设定项的一部分。

Mat A；

A = Mat::zeros （3，3，CV_32F）；

在上面的示例中，只要A不是 3 x 3浮点矩阵它就会被分配新的矩阵。否则为现有的

矩阵 A填充零。

Mat::ones

返回一个指定的大小和类型的全为1的数组。

C++: static MatExpr Mat::ones(int rows, int cols, int type)

C++: static MatExpr Mat::ones(Size size, int type)

C++: static MatExpr Mat::ones(int ndims, const int* sizes, int type)

参数：

ndims –数组的维数。

rows –行数。.

cols –列数。

size –替代矩阵大小规格Size(cols, rows)的方法。

sizes –指定数组的形状的整数数组。

type –创建的矩阵的类型。

该方法返回一个 Matlab 样式 1 的数组初始值设定项，类似Mat::zeros()。请注意，这种方法中你可以使用任意一个值和Matlab 语法初始化数组如下：

Mat A = Mat::ones (100，100，CV_8U) * 3 ；/ / 使100 x 100 矩阵里充满 3。

上述操作不会形成一个 100 x 100 1 的矩阵，然后乘以 3。相反，它只是记住

缩放因子（在本例中 3）在实际调用矩阵初始值设定项时使用它。

叶落西湘

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
复制链接

分享到 QQ

分享到新浪微博

扫一扫

专栏目录

opencv2矩阵操作

存取矩阵元素

矩阵/向量操作