二分法开根号
首先是最基本的二分开根号,这个比较容易理解,复杂度比起下面讲的牛顿迭代法要高,更容易理解。
下面给出代码:
#define eps 0.00001
float SqrtByDichotomy(float n)
{
if(n<0)
{
return -1.0;
}
else
{
float low,up,mid,last;
low=0,up=(n>=1?n:1);
mid=(low+up)/2;
do
{
if(mid*mid>n)
up=mid;
else
low=mid;
last=mid;
mid=(up+low)/2;
}while(fabsf(mid-last) > eps); //求浮点数x的绝对值
return mid;
}
}牛顿迭代法
这个算法的复杂度比二分法低。
牛顿迭代法——百度百科里面讲的很清楚。
设r是 的根,选取 作为r的初始近似值,过点 做曲线 的切线L,L的方程为 ,求出L与x轴交点的横坐标 ,称x1为r的一次近似值。过点 做曲线 的切线,并求该切线与x轴交点的横坐标 ,称 为r的二次近似值。重复以上过程,得r的近似值序列,其中, 称为r的 次近似值,上式称为牛顿迭代公式。
如果只是开根号运算的话,迭代公式为:
double SQR(double a){
double x=a,y=0.0;
while(fabs(x-y)>0.00001){
y=x;
x=0.5*(x+a/x);
}
return x;
}
还有其他算法先不看了,感觉把这两种弄明白差不多了,有一种Carmack算法精度不够,但是复杂度低,感兴趣的时候可以看看。








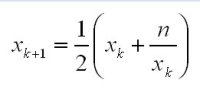
















 5994
5994

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








