参考自:http://my.oschina.net/luckid/blog/382615?fromerr=jJ44fzFI
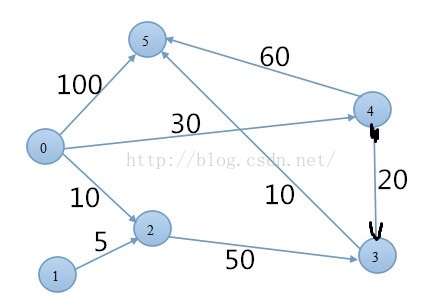
图 如图所示
邻接矩阵如图所示:
代码如下:
/**
* Created by HuLuo on 2016/2/16.
*/
/*
* 单源顶点最短路径问题求解:
* 最短路径问题:给定带权有向图G和源点v0,求从v0到图中其他各顶点的最短距离.
* Dijkstra算法:按路径长度递增的方法计算某一点到其余各点的最短距离。
*/
public class Dijkstra
{
/*
* max:给出的极大值,表示顶点之间无法到达
* dist[]:存储最短路径长度的数组
* prve[]:存储当前顶点的前驱顶点
* a[][]:给定测试的邻接矩阵表
*/
private static int max = Integer.MAX_VALUE;
private static int dist[] = new int[6];
private static int prve[] = new int[6];
private static int a[][] = { { 0, max, 10, max, 30, 100 }, { max, 0, 5, max, max, max }, { max, max, 0, 50, max, max }, { max, max, max, 0, max, 10 }, { max, max, max, 20, 0, 60 }, { max, max, max, max, max, 0 } };
//dijkstra算法
public void dijkstra(int v, int[][] a, int dist[], int prve[])
{
int n = dist.length - 1;
//s[]:存储已经找到最短路径的顶点,false为未求得
boolean[] s = new boolean[n + 1];
for(int i = 1; i <= n; i++)
{
//初始化dist[]数组
dist[i] = a[v][i];
s[i] = false;
/*
* prve[]数组存储源点到顶点vi之间的最短路径上该顶点的前驱顶点,
* 若从源点到顶点vi之间无法到达,则前驱顶点为-1
*/
if(dist[i] < Integer.MAX_VALUE)
prve[i] = v;
else
prve[i] = -1;
}
dist[v] = 0; //初始化v0源点属于s集
s[v] = true; //表示v0源点已经求得最短路径
for(int i = 1; i <= n; i++)
{
int temp = Integer.MAX_VALUE; //temp暂存v0源点到vi顶点的最短路径
int u = v;
for(int j = 1; j <= n; j++)
{
if(( !s[j] ) && dist[j] < temp)
{ //顶点vi不属于s集当前顶点不属于s集(未求得最短路径)并且距离v0更近
u = j; //更新当前源点,当前vi作为下一个路径的源点
temp = dist[j]; //更新当前最短路径
}
}
s[u] = true; //顶点vi进s集
//更新当前最短路径以及路径长度
for(int j = 0; j <= n; j++)
{
if(( !s[j] ) && a[u][j] < Integer.MAX_VALUE)
{ //当前顶点不属于s集(未求得最短路径)并且当前顶点有前驱顶点
int newDist = dist[u] + a[u][j]; //累加更新最短路径
if(newDist < dist[j])
{
dist[j] = newDist; //更新后的最短路径
prve[j] = u; //当前顶点加入前驱顶点集
}
}
}
}
}
//结果输出方法
/*
* m:源点
* []p:更新结果后的前驱顶点集
* []d:更新结果后的最短路径集
*/
public void outPath(int m, int[] p, int[] d)
{
for(int i = 0; i < dist.length; i++)
{
//当前顶点已求得最短路径并且当前顶点不等于源点
if(d[i] < Integer.MAX_VALUE && i != m)
{
System.out.print( "v" + i + "<--" );
int next = p[i]; //设置当前顶点的前驱顶点
while(next != m)
{ //若前驱顶点不为一个,循环求得剩余前驱顶点
System.out.print( "v" + next + "<--" );
next = p[next];
}
System.out.println( "v" + m + ":" + d[i] );
}
//当前顶点未求得最短路径的处理方法
else if(i != m)
System.out.println( "v" + i + "<--" + "v" + m + ":no path" );
}
}
public static void main(String[] args)
{
// TODO Auto-generated method stub
Dijkstra d = new Dijkstra();
d.dijkstra( 0, a, dist, prve );
d.outPath( 0, prve, dist );
}
}
参考自:http://my.oschina.net/luckid/blog/382615?fromerr=jJ44fzFI








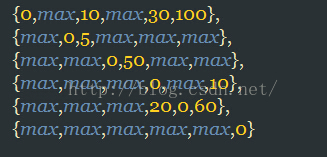














 3170
3170

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








